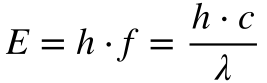“Se a Mecânica Quântica ainda não o chocou profundamente, você ainda não a entendeu.”
Niels Bohr
A Mecânica Quântica estuda a estrutura da matéria nas escalas atômica e subatômicas, e a suas interações com a energia. Portanto, ela se tornou a base teórica para o estudo dos materiais, principalmente os elétricos e magnéticos.
História da Mecânica Quântica
Procuramos o sol no inverno para nos aquecer e a sombra no verão para nos refrescar. O sol fornece a energia que atinge a terra através do espaço.
A brasa brilhante na churrasqueira se encontra muito quente, mas o carvão que não brilha também pode nos queimar (Figura 1).
Portanto, os materiais devem estar acima de determinada temperatura para brilhar e a cor muda com a temperatura.
Denomina-se Radiação este fenômeno de transferência de calor, que associa temperatura e luz, e ocorre sem a necessidade de existir um meio material.

Em 1887, Hertz observou que uma chapa metálica liberava cargas negativas quando recebia luz ultravioleta. Esta corrente elétrica podia ser interrompida aplicando-se uma tensão. O valor desta tensão independia do brilho, mas dependia da frequência da luz.
Este fenômeno ficou conhecido como efeito fotoelétrico.
A brasa mostra que a energia depende da cor e o efeito fotoelétrico mostra que a energia depende da frequência.
Logo, cor, frequência, e energia se encontram relacionados.
Planck
A relação entre energia e frequência deu a Planck o prêmio Nobel de Física de 1918.
Evidentemente, ninguém ganha o prêmio Nobel sem matemática. Planck estabeleceu que a energia se relacionava com a frequência através de uma constante, denominada em sua homenagem de constante de Planck, conforme mostra a Equação 1.
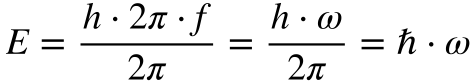
Onde:
-
- E é a energia [J];
- h é a constante de Planck [6,626 069 57 E-34 J.s];
- h cortado é a constante de Planck dividida por 2π;
- f é a frequência [Hz];
- c é a velocidade da luz [299 792 458 m/s];
- λ é o comprimento de onda [m];
- ω é a frequência angular [rad/s].
Einstein
Einstein demonstrou que o aumento da energia das cargas retiradas pelo efeito fotoelétrico depende do aumento da frequência da luz (sua energia). Além disso, a energia da luz deveria ser maior do que a energia que mantinha a carga presa ao metal.
Isto deu a Einstein o Prêmio Nobel de Física de 1921.
Bohr
Bohr deu um passo adicional na construção da mecânica quântica em 1913 ao aplicar os conceitos de Planck no modelo atômico de Rutherford e ganhou seu prêmio Nobel de Física de 1922.
Energia e momento consistem em conceitos básicos da física.
A física clássica define o Momento Linear – p – 1como massa vezes a velocidade e o Momento Angular – L – 2como o momento de inércia vezes a velocidade angular ou o produto vetorial da posição pelo momento linear.
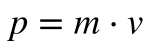
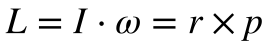
Onde:
-
- p é o momento linear;
- m é a massa da partícula;
- v é a velocidade da partícula;
- L é o momento angular;
- I é o momento de inércia;
- ω é a velocidade angular da partícula;
- r é o vetor posição.
Por outro lado, a Equação 4 relaciona a energia cinética com o momento.
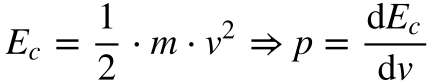
Onde:
-
- Ec é a energia cinética;
- p é o momento;
- m é a massa;
- v é a velocidade.
Como energia e momento se encontram relacionados, Bohr aplicou a equação de Planck ao momento angular.
Apenas as órbitas com momento angular igual aos valores da equação de Bohr seriam estáveis.
Este conceito representou o primeiro choque da mecânica quântica; a energia e o momento angular se tornaram grandezas discretas.
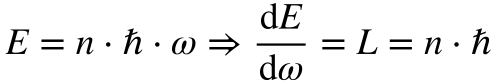
Onde:
-
- E é a energia;
- L é o momento angular;
- n é um número inteiro maior que zero;
- h cortado é a Constante de Planck dividida por 2π;
- ω é a velocidade angular;
A partir da Equação 3 do Capítulo Átomos, que descreve a velocidade do elétron do modelo de Rutherford, Bohr formulou as expressões abaixo, que fornecem a velocidade e o raio do elétron do átomo de hidrogênio.
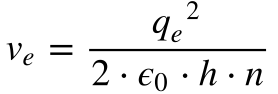
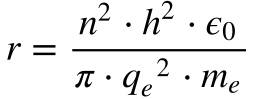
Onde:
-
- ve é a velocidade do Elétron;
- qe é a carga do Elétron;
- ε0 é a permissividade elétrica no vácuo;
- h é a Constante de Planck;
- me é a massa do Elétron;
- n é um número inteiro maior que zero.
Exercício Proposto
Calcule a velocidade do Elétron e seu raio para n=1 e compare com os resultados obtidos com a fórmula do Capítulo Átomos e com o raio teórico do hidrogênio.
A energia total do elétron consiste na soma das suas energias cinética e potencial. A Equação 4 fornece a energia cinética e a Equação 8 a energia potencial eletrostática:
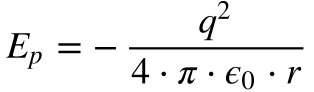
Onde:
-
- q é a carga elétrica;
- r é a distância;
- ε0 é a permissividade elétrica no vácuo;
Desta maneira, a Equação 9 fornece a energia total do elétron.
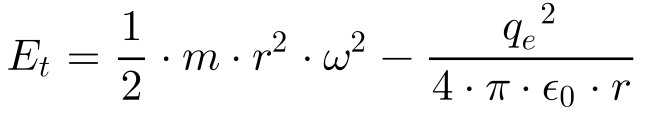
As equações 10 e 11 apresentam a força de atração eletrostática do proton e elétron do átomo de hidrogênio do modelo de Rutherford e a força centrípeta.
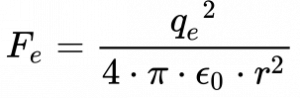
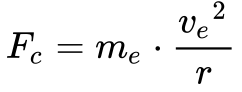
De acordo com Wolf3, Equação 12 fornece o equilíbrio entre força de atração eletrostática e a força centrípeta.
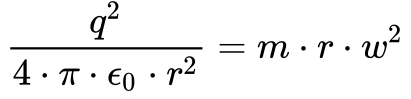
Substituindo a Equação 12 na Equação 9, obtêm-se que a energia total do elétron equivale à metade da energia potencial, conforme mostra a Equação 13.
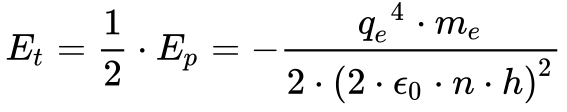
Além disso, a energia total possui sempre valores negativos, demonstrando a estabilidade do sistema, e tende a zero quando o raio e n tendem para infinito.
A energia potencial negativa decorre da escolha da referência zero para distância infinita porque a força eletrostática diminui com a distância.
Reflexão
Será que isto explica o número máximo de linhas na Tabela Periódica?
-
- Calcule o valor desta energia para n=8.
- Calcule a diferença de energia dos níveis 7 e 8.
- Compare com a energia refletida pela terra a 25 ºC sobre a área deste átomo.
Apesar do sucesso na época, o modelo de Bohr ainda apresentava lacunas, que ele contornou postulando as seguintes condições:
-
- As expressões somente valem para órbitas discretas com determinados níveis de energia;
- Nessas órbitas não existe o fenômeno de emissão de radiação eletromagnética;
- A mudança de órbita do Elétron somente seria possível pela absorção ou emissão de energia em múltiplos inteiros de h x f.
A partir desses postulados Bohr determinou o raio das órbitas dos elétrons de acordo com a Equação 14.
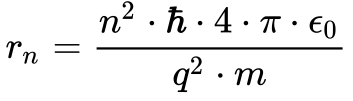
Observem que esta expressão equivale à Eq. 7 e a única diferença consiste na utilização de h cortado no lugar de h.
Denomina-se o número n de número quântico principal.
No caso de n=1, a Equação 15 representa o valor do raio da órbita do Elétron do Hidrogênio e se tornou conhecida como Raio de Bohr.
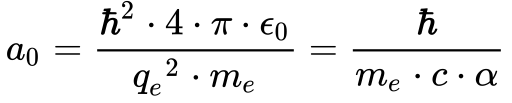
Onde:
A beleza da teoria de Bohr consiste em apresentar a primeira estimativa teórica da distância entre o núcleo e o elétron do átomo envolvendo apenas constantes físicas.
Mas como comprovar que este cálculo se encontra correto?
Bohr na prática
O Capítulo Átomos apresentou a Emissão Atômica e os resultados experimentais de Rydberg.
A constante de Rydberg obtida originalmente de forma experimental foi de 109 677,581 0 cm-1 6.
Comparando a Equação 6 no Capítulo Átomos com a Equação 1 deste capítulo, obtem-se que7:
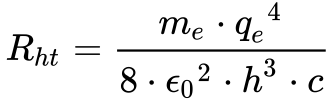
A diferença entre o valor experimental e o teórico é de apenas 0,05%.
Portanto, a teoria de Bohr passou em seu primeiro teste prático.
Substituindo a Equação 16 na Equação 15, a energia dos níveis do átomo de Hidrogênio em função da constante de Rydberg ocorre da seguinte maneira:
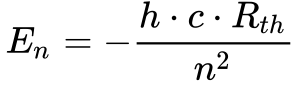
A Figura 15 mostra que os Elétrons absorvem ou emitem energia ao mudarem de nível de acordo com as equações de Bohr. Uma das formas possíveis desta troca de energia ocorre através da absorção ou emissão de luz8, utilizada em LEDs e células fotovoltaicas.
Este fenômeno quântico permitiu a construção de todos os semicondutores responsáveis pela eletrônica, telecomunicações e eletrônica de potência modernos. Além disso, ele gerou outros Prêmios Nobel.
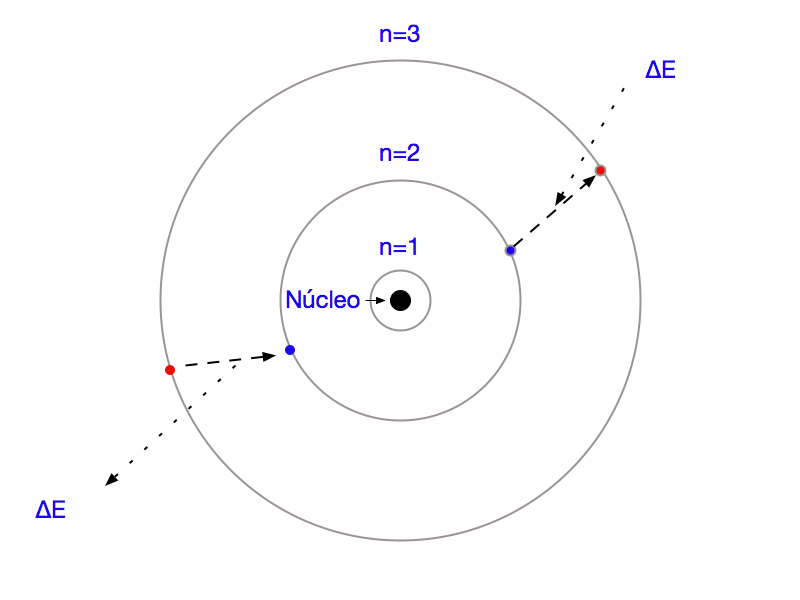
Conforme anteriormente, energia e momento angular se encontram relacionados. Portanto, o momento também se tornou uma grandeza quântica.
Infelizmente o modelo de Bohr não explica o comportamento dos outros átomos com mais Prótons e Elétrons, e, desta maneira, concluímos o estudo da “velha teoria quântica” 9. Talvez velha para os físicos, mas moderna para os engenheiros.
Material complementar
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]e5_V78SWGF0[/wpdevart_youtube]
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]FlIrgE5T_g0[/wpdevart_youtube]
Referências
- EINSTEIN, A., On a Heuristic Point of View about the Creation and Conversion of Light, Ann. Physik 17,132, 1905.
- HAAR, T., The Old Quantum Theory, Pergamon, 1967.
- KREYSZIG, E. Advanced Engineering Mathematics, 9 edição, John Wiley & Sons, 2006.
- MILLER, D.A.B, Quantum Mechanics for Scientists and Engineers, Cambridge University Press, 2008.
- WOLF, H., Atomic and Quantum Physics, 2 edição, Springer-Verlag, 1987.
- Imagem de <a href=”https://pixabay.com/pt/users/geralt-9301/?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=7854066″>Gerd Altmann</a> por <a href=”https://pixabay.com/pt//?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=7854066″>Pixabay</a>
- Imagem de <a href=”https://pixabay.com/pt/users/geralt-9301/?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=3871218″>Gerd Altmann</a> por <a href=”https://pixabay.com/pt//?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=3871218″>Pixabay</a>
- Imagem de <a href=”https://pixabay.com/pt/users/inggwolf-283834/?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=362944″>Guido Wolf</a> por <a href=”https://pixabay.com/pt//?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=362944″>Pixabay</a>