Condutividade Elétrica CC

“Descobertas decorrem de acidentes que encontram mentes preparadas.”

Albert Szent-Gyorgyi

Os materiais elétricos dominam o mundo devido à sua capacidade de conduzir eletricidade, denominada de condutividade elétrica.

Os cabos elétricos conectam as usinas de geração de energia a todos os consumidores no planeta, e os telefones fixos não funcionariam sem os cabos telefônicos.

Resistências elétricas transformam eletricidade em calor. O chuveiro elétrico, o ferro de passar roupas, o secador de cabelos, o forno elétrico, e o fogão elétrico fazem parte do conjunto de equipamentos onde a resistência elétrica representa o elemento primordial para seu funcionamento. Além disso, resistências elétricas atuam como coadjuvantes no funcionamento dos equipamentos eletrônicos e telecomunicações, tais como televisão, computador, e telefone celular.

Resistividade e Condutividade Elétricas

Por se tratar de uma grandeza extensiva, a ciência dos materiais não utiliza a resistência elétrica porque seu valor depende das dimensões do material.

Contudo, a Equação 1 transforma a resistência elétrica numa grandeza intensiva relativa ao volume, denominada de resistividade elétrica volumétrica.

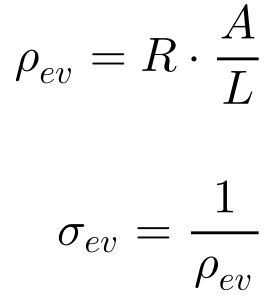
Onde:

• • R é a resistência elétrica [Ω].
  • A é a área da seção reta do condutor perpendicular ao fluxo da corrente elétrica [m²].¹
  • L é o comprimento do condutor na direção da corrente elétrica[m].
  • σ_ev é a condutividade elétrica volumétrica do material [S/m].
  • ρ_ev é a resistividade elétrica volumétrica do material [Ω.m].

Outra forma de definir a resistividade elétrica consiste na utilização da massa do material de acordo com a Equação 2. Observa-se que a resistividade mássica equivale à resistividade volumétrica multiplicada pela massa específica do material.

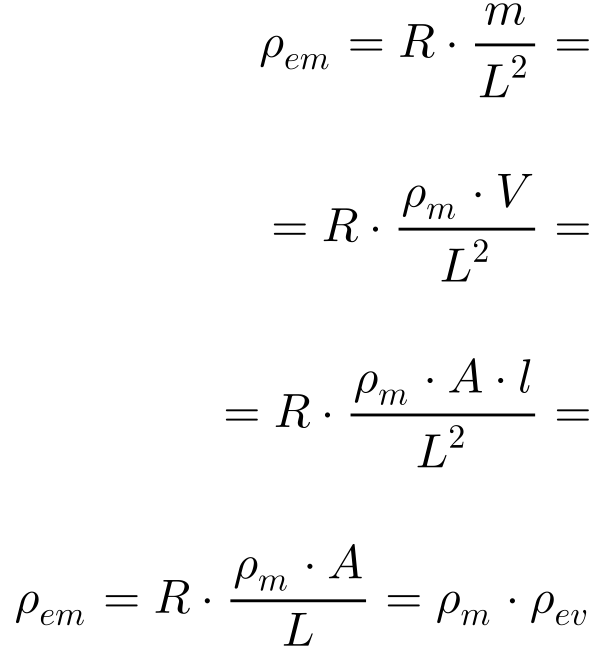
Onde:

• R é a resistência elétrica [Ω].
• ρ_em é a resistividade elétrica mássica [Ω.kg/m²].
• A é a área da seção reta do condutor perpendicular ao fluxo da corrente elétrica [m²].
• L é o comprimento do condutor na direção da corrente elétrica[m].
• ρ_m é a massa específica[kg/m3].
• ρ_ev é a resistividade elétrica volumétrica do material [Ω.m].

Portanto, a massa específica relaciona as duas propriedades elétricas.

Modelo de Drude

Em 1827, Georg Ohm formulou sua famosa Lei, baseado em resultados empíricos, que relaciona tensão e corrente num condutor. De acordo com sua teoria, essa relação se mantém constante e foi denominada de Resistência Elétrica. Contudo, ela depende do material e varia em função de energias externas.

A descoberta do Elétron revolucionou a física em 1897, e Paul Drude publicou, em 1900², sua teoria sobre a condução elétrica reunindo as novas descobertas da Física com o conhecimento empírico de Ohm. Os átomos de metais sólidos se mantêm unidos através da ligação metálica, onde os elétrons de valência permanecem livres para circular em todo o material.

Por isso, ele aplicou a mecânica clássica aos “elétrons livres”, para explicar os fenômenos de condução elétrica e térmica, e a Valência Química, proposta em 1884 para designar a capacidade de associação química entre elementos.

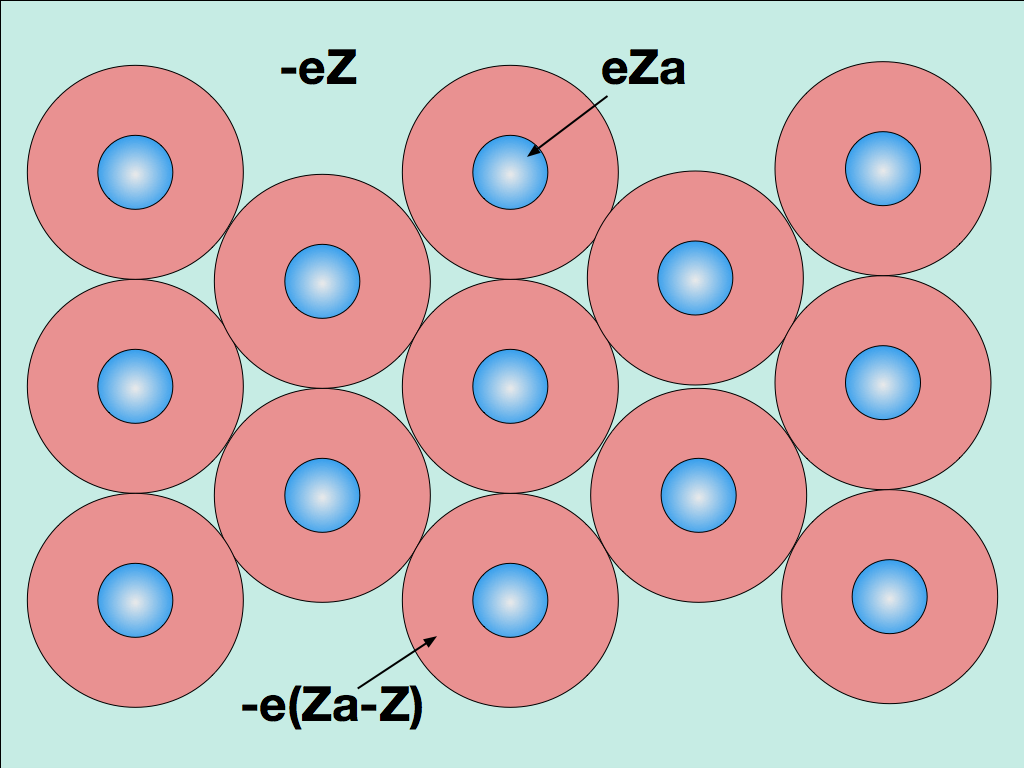
A Figura 1 ilustra o conceito utilizado por Drude.

O núcleo do átomo (azul) possui uma carga positiva proporcional ao número atômico do material (Za) e à carga do Elétron (e). O núcleo se encontra fixo na estrutura cristalina do material. Essa hipótese, apesar de falsa, consiste numa primeira aproximação que explica alguns fenômenos.

Os elétrons se encontram ao redor do núcleo, que foram divididos em dois grupos, os Elétrons de Valência (Z em verde) e os demais (Z_a em vermelho). 

---

Revisão

1. Como se determinam os elétrons de valência dos elementos do grupo principal da tabela periódica?
2. Como se determinam os Elétrons de Valência dos Elementos de Transição da tabela periódica?

---

Drude considerou que os elétrons livres, poderiam se movimentar por todo o material como moléculas de um gás³, colidindo eventualmente com as esferas fixas dos elétrons presos ao núcleo. 

O primeiro passo da teoria de Drude consistiu em estimar a densidade desse “gás” eletrônico da seguinte maneira:

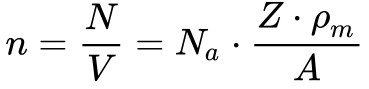
Onde:

• • n é a densidade de Elétrons Livres [elementos/m³].
  • N é o número total de Elétrons Livres [elementos].
  • V é o volume total do material [m³].
  • N_a é a constante de Avogadro [elementos/mol];
  • Z é número de Elétrons de Valência [elementos].
  • ρ_m é a densidade do material [kg/m³].
  • A é a massa atômica do material [g/mol].

Este modelo utilizou as seguintes premissas:

• • Os elétrons livres não interagem com outros elétrons nem com os íons nos intervalos entre colisões;
  • A repulsão elétrica entre os elétrons livres e os íons altera abruptamente apenas a direção do Elétron e, como numa colisão elástica ⁴ , a energia permanece constante;
  • O tempo médio entre colisões, denominado de tempo de relaxação, tempo entre colisões, ou tempo médio livre constitui parâmetro fundamental do modelo.
  • O equilíbrio térmico dos elétrons ocorre apenas através das colisões.

---

Exercício Proposto

Faça um gráfico da densidade de elétrons livres de seis metais com elevada condutividade e seis com baixa.

---

Modelo para Corrente Contínua

Considerando todos os elétrons se movendo com velocidade v, a densidade de corrente possuirá a mesma direção, conforme mostra a Figura 2, e a Equação 4 fornece a quantidade de cargas atravessando a área perpendicular à velocidade das partículas -A.

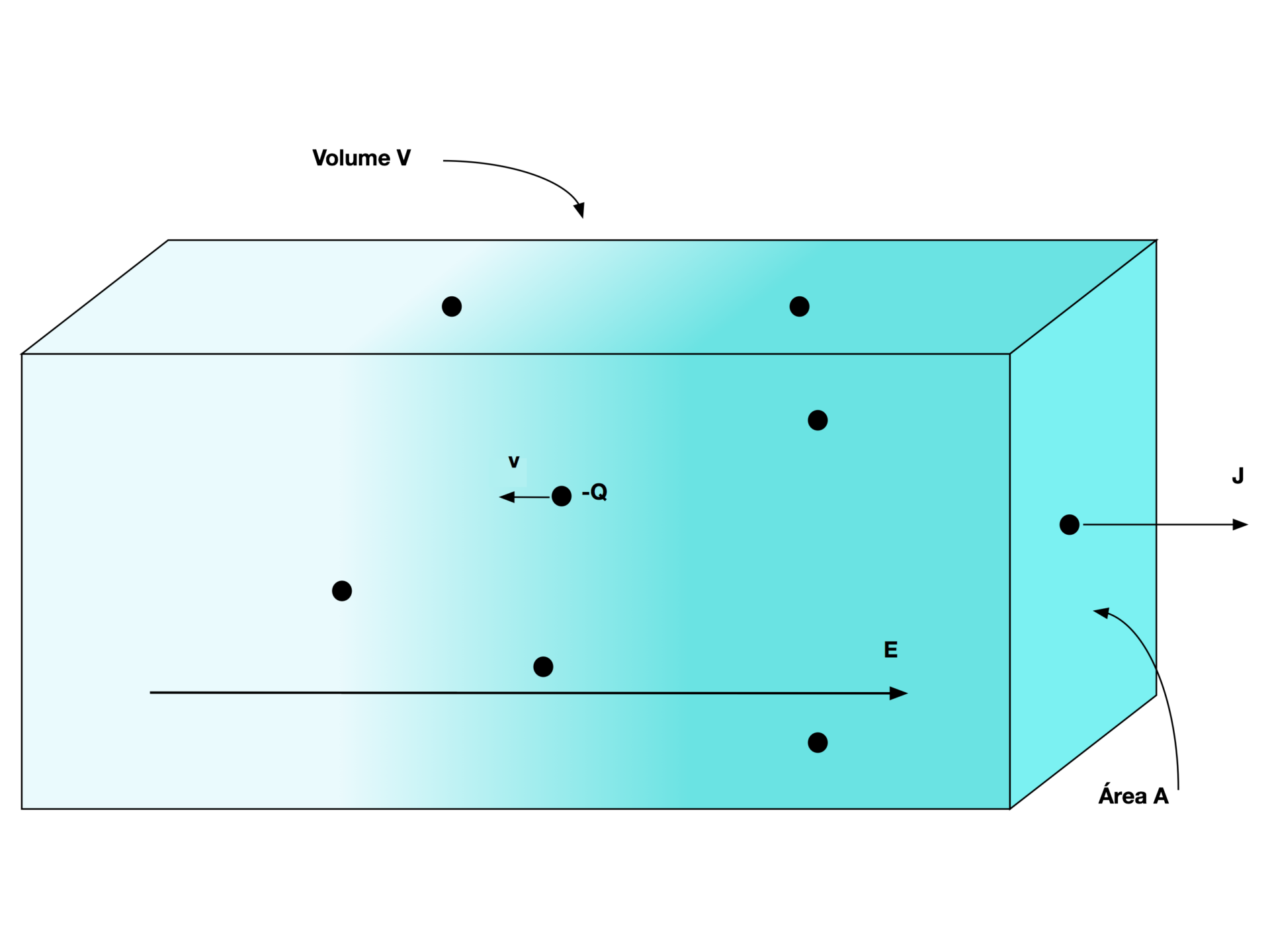
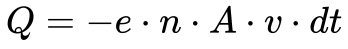
Onde:

• • Q é a quantidade de cargas atravessando a área A [C];
  • e é a carga elementar [1,602 1766 3×10^-19C];
  • n é a densidade de Elétrons Livres [elementos/m³];
  • A é a área perpendicular ao fluxo da corrente [m²]
  • v é a velocidade média dos Elétrons Livres ocasionada pelo campo elétrico [m/s];
  • dt é o intervalo de tempo infinitesimal.

A Equação 5, obtida a partir da Equação 4, fornece a densidade da corrente.

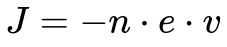
Onde:

• • J é a densidade de corrente [A/m²]
  • e é a carga elementar [1,602 1766 3×10^-19C];
  • n é a densidade de Elétrons Livres [elementos/m³];
  • v é a velocidade média dos Elétrons Livres ocasionada pelo campo elétrico [m/s].

Contudo, os elétrons se movem em direções aleatórias e com velocidades proporcionais à energia térmica e ao campo elétrico aplicado. Por isso, torna-se necessário considerar essas duas componentes separadamente.

Determina-se a componente da velocidade dos elétrons referente à temperatura – v_t – a partir da Teoria Cinética dos Gases ⁵ considerando a energia cinética dos elétrons igual à energia cinética dos gases, de acordo com a Equação 6.

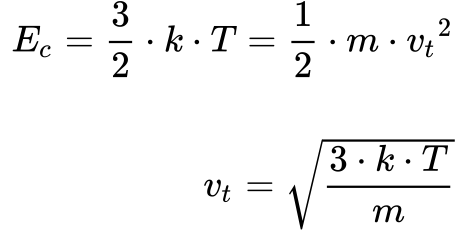
Onde:

• • v_t é a velocidade térmica [m/s]
  • k é a constante de Boltzmann [1,380 649×10^-23 J/K];
  • T é a temperatura [K]
  • m é a massa do Elétron [9,109 383 70×10^-31 kg];

---

Reflexão

Estime a velocidade térmica do elétron de acordo com a Equação 6 e compare com a velocidade calculada a partir da Equação 6 do Capítulo de Mecânica Quântica. 

---

Por outro lado, um campo elétrico aplicado ao Elétron produzirá uma força dada por:

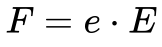
De acordo com a Física Clássica, força constante provoca aceleração constante. Sem nenhuma outra força presente, esta aceleração levaria os Elétrons a velocidades sempre crescentes.

Como Ohm verificou que a corrente permanecia finita, existe outra força atuando para anular a aceleração média nos elétrons livres.

Em função disso, Drude propôs a existência de uma força de atrito decorrente da colisão dos elétrons livres com os íons do material.

A Física Clássica relaciona força com velocidade da seguinte maneira:

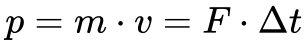
Onde: 

• • p é o momento linear;
  • m é a massa;
  • v é a velocidade;
  • F é a força;
  • Δt é um intervalo de tempo.

Para utilizar este conceito, Drude considerou a existência de colisões elásticas entre os elétrons livres e os íons do material ocorrendo, na média, a cada intervalo de tempo médio τ.

Este intervalo de tempo se tornou conhecido como tempo de relaxação porque representa o tempo médio gasto para os Elétrons Livres perderem o momento adquirido pela ação do campo elétrico.

A Mecânica Clássica associa força a variações de momento da seguinte maneira:

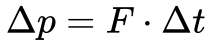
Onde:

• • Δp é a variação do momento linear;
  • F é a força;
  • Δt é o intervalo de tempo.

Desta maneira, as colisões dos elétrons resultariam numa força contrária à força eletrostática – F_r– de acordo com a Equação 9.

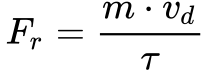
Igualando as equações 7 e 10, obtem-se a velocidade de deriva, conforme mostrado na Equação 11.

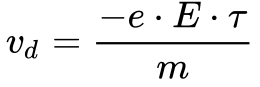
Onde:

• • v_d é a velocidade de deriva[m/s];
  • e é a carga elementar [1,602 1766 3×10^-19C];
  • E é o campo elétrico [V/m];
  • τ é o tempo de relaxação[s];
  • m é a massa do Elétron [9,109 383 70×10^-31 kg];

De acordo com a Equação 11, a Velocidade de Deriva depende do campo elétrico, uma grandeza extrínseca ao material.

Portanto, criou-se o conceito de Mobilidade dos Elétrons – μ, uma grandeza intrínseca para caracterizar a resistência produzida pelas colisões dos Elétrons Livres nos materiais.

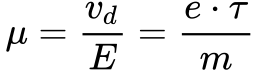
Onde:

• • μ é a mobilidade dos Elétrons[m²/(V.s)];
  • e é a carga elementar [1,602 1766 3×10^-19 C];
  • τ é o tempo de relaxação[s];
  • m é a massa do Elétron [9,109 383 70×10^-31 kg];

Obtem-se a Equação 13 substituindo a Equação 12 na Equação 5. Desta maneira, Drude forneceu uma explicação teorica para a Lei de Ohm. 

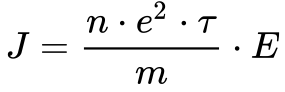
Onde:

• • n é a densidade de elétrons livres [elementos/m³]⁶;
  • e é a carga elementar [1,602 1766 3×10^-19C];
  • τ é o tempo de relaxação [s];
  • m é a massa do Elétron [9,109 383 70×10^-31 kg];
  • E é o campo elétrico [V/m].

Finalmente, a equação 14 fornece o valor da condutividade e da resistividade em função apenas das propriedades do material.

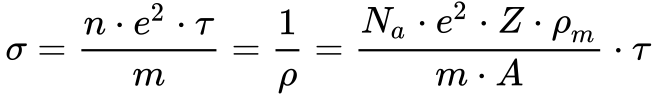
Onde:

• • σ é a condutividade do material [S/m];
  • n é a densidade de Elétrons Livres [elementos/cm³];
  • e é a carga elementar [1,602 1766 3×10^-19C];
  • τ é o tempo de relaxação [s].
  • m é a massa do Elétron [9,109 383 70×10^-31 kg];
  • ρ é a resistividade do material [Ω.m];
  • N_a é a constante de Avogadro [6,022 140 73 × 10²³ 1/mol];
  • Z é número de Elétrons de Valência [elementos];
  • ρ_m é a densidade do material [g/cm³];
  • A é a massa atômica do material [g/mol].

Todos os parâmetros da equação 14 se encontram determinados, exceto o tempo de relaxação – τ.

Contudo, pode-se estimá-lo a partir da medição da condutividade ou resistividade uilizando a Equação 15.

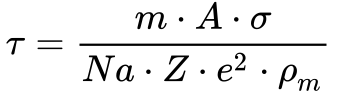
Onde:

• • τ é o tempo de relaxação[s];
  • m é a massa do Elétron [9,109 383 70×10^-31 kg];
  • A é a massa atômica do material [kg/mol].
  • σ é a condutividade do material [S/m];
  • N_a é a constante de Avogadro [6,022 140 73 × 10²³ 1/mol];
  • Z é número de Elétrons de Valência [elementos];
  • e é a carga elementar [1,602 1766 3×10^-19C];
  • ρ_m é a densidade do material [ kg/m³];

 

---

Exercício Proposto

Calcule o tempo de relaxação e este tempo dividido pela condutividade para o Cobre, Prata, Alumínio, Tungstênio, Ouro, Ferro e Chumbo.

---

Conclusões

O Modelo de Drude permitiu explicar a Lei de Ohm, a condutividade elétrica e térmica dos metais, a relação entre condutividade elétrica e térmica, e as propriedades óticas dos metais.

Por outro lado, ela não consegue explicar a condutividade de isolantes e semicondutores, o Efeito Fotoelétrico, a Radiação do Corpo Negro, e o efeito Compton.

Portanto, a Física precisou evoluir com novas teorias.

• Referências

1. ASHCROFT, N.W., MERMIN, N.D., Solid State Physics, Harcourt, 1976.
2. BEATY, H.W., FINK, D.G., Standard Handbook for Electrical Engineers, 15 edição, McGraw-Hill, 2007.
3. CHELIKOWSKY, J.R., COHEN, M.L., Semiconductors: A Pillar of Pure and Applied Physics, Journal of Applied Physics 117, 112812 (2015).⁷
4. HAYNES, W.W., Handbook of Chemistry and Physics, 93 edição, CRC, 2012.⁸
5. KASAP, S.; KOUGHIA C.; RUDA, H.E.; Electrical Conduction in Metals and Semiconductors. In: KASAP, S.; CAPPER, P.(Ed.); Springer Handbook of Electronic and Photonic Materials, Springer, 2017.
6. KITTEL, C., Introduction to Solid State Physics, 8 edição, John Wiley & Sons, 2005
7. NOTAROS, B.M., Eletromagnetismo, Pearson Education do Brasil, 2012.
8. OHRING, M., Engineering Materials Science, Academic Press, 1995.
9. QUINN, J.J., YI, K, Solid State Physics – Principles and Modern Applications, Springer-Verlag, 2009.