Estruturas Cristalinas

“Um diamante com falhas vale mais do que um seixo sem imperfeições”

Provérbio Chinês

As estruturas cristalinas dos sólidos afetam todas as propriedades dos materiais, e a cristalografia fornece a base teórica para o estudo das propriedades dos materiais.

Simetrias internas e forças externas afetam as propriedades dos materiais, e todos os materiais possuem algum tipo de simetria interna, mesmo que não sejam cristalinos.

Os materiais cristalinos apresentam 32 tipos estruturas cristalinas decorrentes das simetrias possíveis, materiais amorfos¹ possuem apenas uma simetria; a esférica. Materiais com simetria esférica possuem propriedades isotrópicas, isto é, independem da direção espacial.

Cerâmicas, metais, rochas e sólidos policristalinos também possuem simetria esférica. Por outro lado, materiais fibrosos apresentam simetria cilíndrica com eixo na direção das fibras.

As principais forças externas que atuam nos materiais são:

• • • tensão mecânica;
    • campo elétrico;
    • campo magnético;
    • temperatura.

 A simetria dos campos, elétrico e magnético, e das tensões, mecânica e de cisalhamento, dependem de configurações externas. Isto significa que esses elementos externos podem apresentar comportamento anisotrópico²

Porém, a temperatura, por ser um escalar, possui simetria esférica e, consequentemente, possui comportamento isotrópico³

Portanto, o estudo das estruturas cristalinas se tornou importante porque materiais anisotrópicos apresentam propriedades distintas dependendo da orientação espacial e deve-se levar em consideração este detalhe no projeto de máquinas e equipamentos que utilizam estes materiais. 

Existem cristais de todos os tamanhos; gigantescos ou minúsculos.

Portanto, noções de Cristalografia, a ciência que estuda os cristais, tornam-se indispensáveis para a compreensão das propriedades dos materiais.

Rede Cristalina

Materiais cristalinos apresentam uma estrutura denominada de Rede Cristalina, que se caracteriza pela repetição infinita de grupos de átomos exatamente iguais quando vistos de qualquer um dos pontos da Rede. Por isso, torna-se impossível distinguir pontos ou regiões em materiais cristalinos. 

O grupo que se repete denomina-se de Base e o conjunto dos pontos no espaço que determinam a localização da Base denomina-se Rede.

Por exemplo, a Figura 4 mostra um papel de parede formado por desenhos sofisticados que se repetem no plano.

• • Quantos grupos existem?
  • Onde se encontra a Rede?
  • Você consegue determinar o início e o fim do desenho?
  • Como os grupos se repetem?
  • Esta figura poderia representar uma Rede Cristalina?

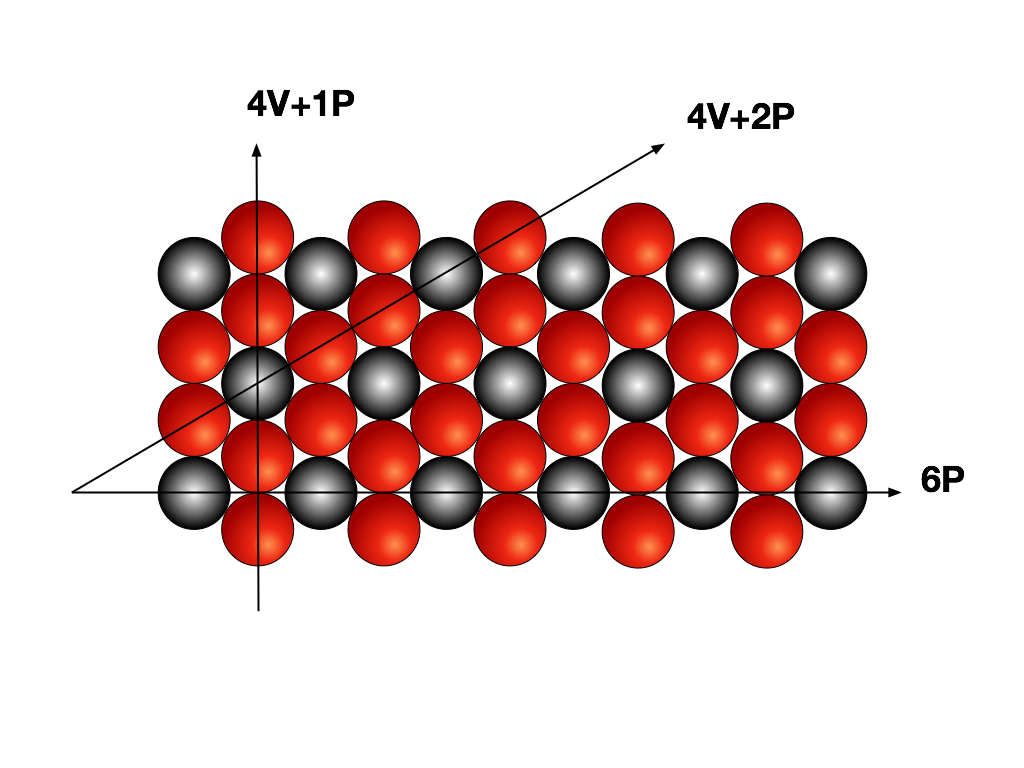
Por outro lado, a Figura 5 representa a estrutura cristalina da molécula de um material condutor fictício.

Se aplicarmos uma corrente elétrica na direção das setas individualmente, mediremos valores distintos de tensão porque o número de moléculas pretas e vermelhas em série depende da direção escolhida.

Isto significa que a resistividade deste material dependerá da direção espacial e deixará de ser uma constante.

O mesmo raciocínio se aplica a outras propriedades do material, tais como a resistividade térmica e o coeficiente de elasticidade.

A Cristalografia estuda a estrutura dos átomos nos sólidos cristalinos através dos seguintes métodos:

• • Difração de Raio-x;
  • Difração de Elétrons;
  • e Difração de Nêutrons.

Cada uma dessas radiações interage de forma diferente com a matéria.

O Raio-X interage com a distribuição espacial dos Elétrons nos Átomos.

Por sua vez, feixes de Elétrons reagem à distribuição de cargas dos Elétrons e Núcleo dos Átomos.

Finalmente, Nêutrons, imunes a campos elétricos, desviam dos núcleos atômicos afetados pela Força Forte. Porém, como os Nêutrons possuem momento magnético, campos magnéticos afetam sua trajetória.

Os videos abaixo descrevem a difração por raios-X, o método mais utilizado na Cristalografia.

A partir da difração de Raios X, a Cristalografia se desenvolveu⁴ porque permitiu medir as dimensões dos cristais com precisão nunca anteriormente possível.

A Figura 6 mostra como o feixe de uma radiação eletromagnética permite medir a distância entre elementos do cristal utilizando a Lei de Bragg – Equação 1.

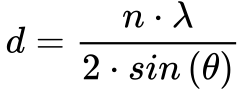
Onde: 

• • n é um número inteiro;
  • λ é o comprimento de onda da radiação incidente;
  • d é a distância entre elementos do cristal;
  • θ é o ângulo medido da radiação refletida.

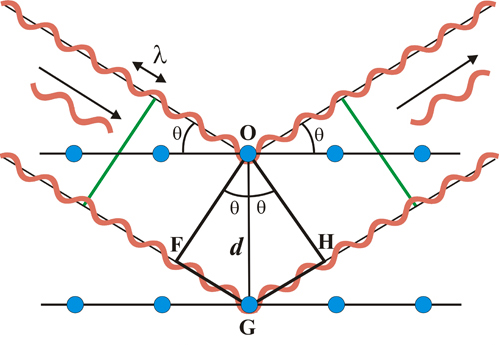
A Cristalografia de Raios X comprovou que os átomos e/ou moléculas dos cristais formavam estruturas geométricas periódicas, e a matemática fornece ferramentas para o estudo dessas figuras geométricas. 

Célula Cristalográfica

A Cristalografia baseia-se nos conceitos de Rede, Grupo e Células.

Vetores de posição definem os pontos da Rede da seguinte maneira:

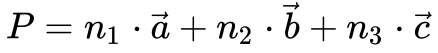
Onde:

• • P é o ponto da Rede Cristalina;
  • n_i são as coordenadas do ponto;
  • a, b e c são os vetores unitários que geram a Rede Cristalina.

A Álgebra Linear fornece os fundamentos para os vetores unitários, sendo os sistemas ortogonais, cilíndricos e esféricos os mais conhecidos.

Porém, existem outros sistemas, que se relacionam através de transformações matemáticas matriciais.

As coordenadas n são números que representam a distância existentes entre a origem do sistema de coordenadas[efn]A origem do sistema de coordenadas pode ser qualquer ponto da Rede[/efn_note] e o ponto em cada uma das direções a, b e c.

Denomina-se de Rede Primitiva a rede onde as coordenadas n são números inteiros e todos os pontos da rede podem ser obtidos como translação dos vetores unitários.

Porém, os pontos da Rede Cristalina necessitam de referência, e o sistema de coordenadas define a referência geométrica.  

O sistema de coordenadas pode ser cartesiano, esférico ou cilíndrico, e a orientação dos eixos obedece a regra da mão direita ou esquerda, dependendo do referencial escolhido.

Normalmente, utiliza-se o referencial da mão direita. 

A determinação da Base da estrutura cristalina ocorre após a identificação dos eixos da Rede Cristalina.

Por exemplo, a Figura 7 apresenta possíveis eixos para a estrutura cristalina, porém apenas os vermelhos poderiam ser utilizados.

O eixo azul viola o princípio da Rede Primitiva.

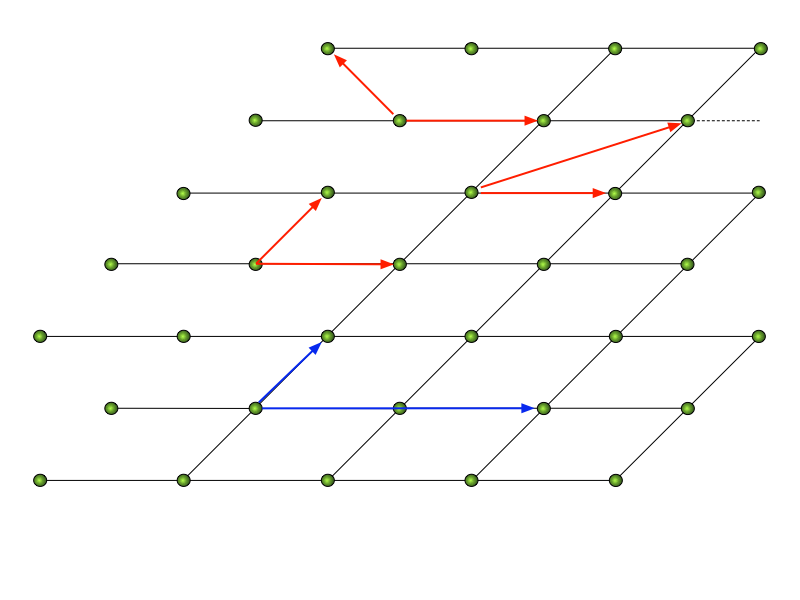
A quantidade de átomos ou moléculas na Base pode ser maior ou igual a um e ajusta-se à origem dos eixos para coincidir com o centro de um dos átomos.

A Célula representa o elemento geométrico básico da rede cristalina e pode ser composto por:

• • átomos iguais;
  • grupos de átomos diferentes;
  • moléculas;
  • íons;
  • grupos de moléculas diferentes.

Célula Unitária

Define-se Célula Unitária como figura geométrica regular, formada por pontos da Rede Cristalina, capaz de formar outras formas geométricas apenas por translação e sem deixar nenhum espaço vazio.

Porém, a natureza nos contempla com diversas formas, que preferem formas mais compactas, simétricas e resistentes.

Por exemplo, o casco das tartarugas apresenta hexágonos, paralelogramos, e trapézios, todas figuras geométricas regulares capazes de formar uma figura geométrica complexa, mas finita.

As abelhas constroem suas colmeias como hexágonos iguais há milhares de anos, que podem se estender infinitamente.

Aranhas criam teias extremamente resistentes com fios em catenárias, que apresentam limitações de crescimento.

E a natureza criou cristais maravilhosos a partir de formas geométricas básicas.

Mas qual seria a forma geométrica capaz satisfazer a condição de possuir geometria regular e formar outras formas geométricas apenas por translação sem deixar nenhum espaço vazio? 

Apenas o Paralelepípedo⁵ – Figura 12, que possui seis faces formadas por paralelogramos, sendo três pares congruentes e paralelos. ⁶ Os três ângulos – α, β, γ – e os três comprimentos – a, b, c – caracterizam a célula e denominam-se constantes da célula ou rede.

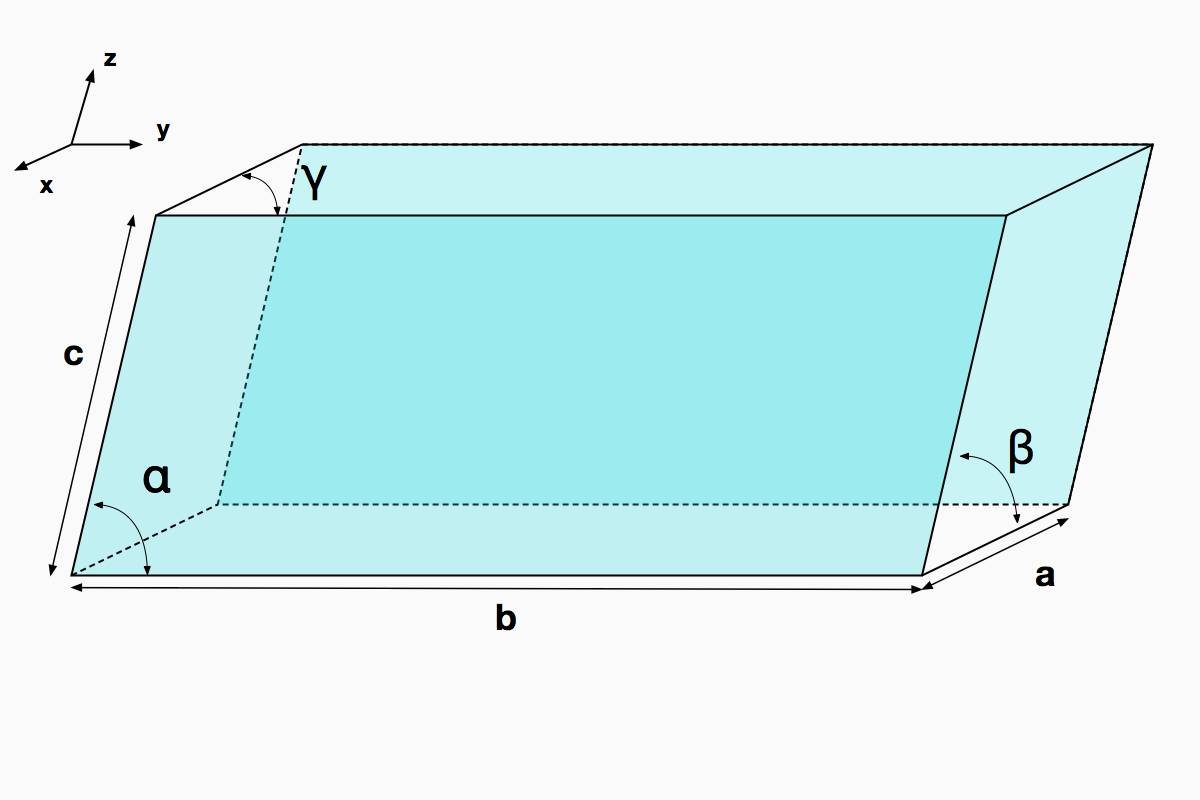
Observa-se que os eixos do sistema cartesiano utilizam a orientação da regra da mão direita⁷ Adicionalmente, os eixos de referência da célula unitária encontram-se paralelos às faces do paralelepípedo e, consequentemente, não são necessariamente ortogonais.

Toda a teoria dos cristais se baseou em geometria e matemática. Por isso, deve-se seguir rigorosamente as convenções e as regras envolvidas.

Mas onde ficam os átomos e moléculas na célula unitária? Para que a representação represente o material desejado, a célula unitária deverá conter a fórmula química da molécula que desejamos representar.

Referências

1. QUINN, J.J., TI K.S., Solid State Physics – Principles and Modern Applications, Springer-Verlag, 2009.
2. NEWNHAM, R.E., Properties of Materials – Anisotropy, Symmetry, Structure, Oxford University Press, 2005.
3. KITTEL, C., Introduction to Solid State Physics, Wiley, 2005.
4. ASHCROFT,N.W., MERMIN, D.,  Solid State Physics, Harcourt, 1976.