“Uma vez que podemos produzir todos os tipos de luz por meio de corpos quentes, podemos atribuir, à radiação em equilíbrio térmico com corpos quentes, a temperatura desses corpos e, portanto, toda radiação, mesmo aquela proveniente de um corpo fosforescente, tem uma certa temperatura para cada cor.”
Wilhelm Wien
A radiação térmica consiste na radiação eletromagnética gerada pelo movimento térmico das partículas eletricamente carregadas que formam a matéria. Portanto, toda matéria, com temperatura superior ao zero absoluto, emite radiação eletromagnética e a transferência de energia ocorre mesmo através do vácuo.
Exemplos importantes desta forma de transferência de calor são:
-
- o aquecimento da terra pelo sol;
- a lâmpada incandescente.
Por se tratar de um fenômeno relacionado a partículas da matéria, seu comportamento somente foi explicado pela física quântica.
A Figura 1 apresenta o espectro eletromagnético e a Figura 2 o espectro da luz visível.
Observa-se que o espectro da luz visível ocupa uma minúscula parcela do espectro eletromagnético dentro da faixa da radiação térmica.
Portanto, surge a questão: por que nossa visão capta apenas esta parcela do espectro eletromagnético?
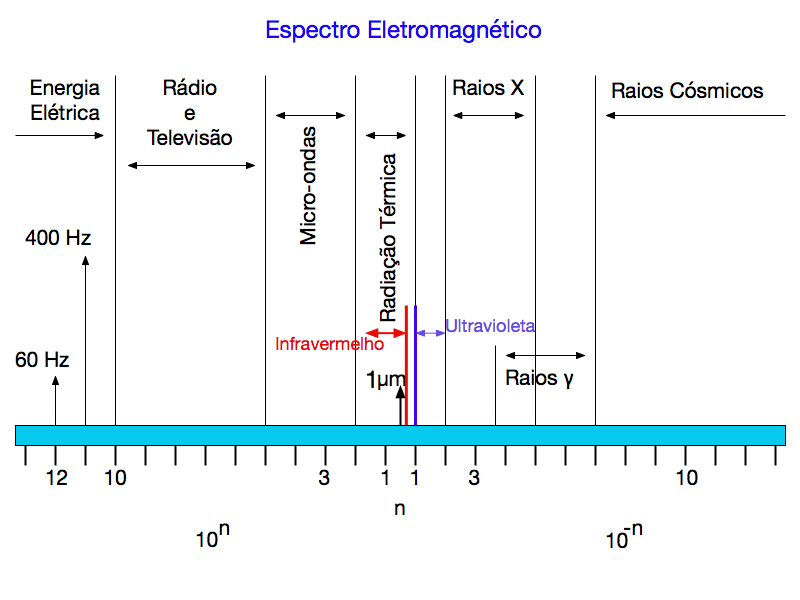
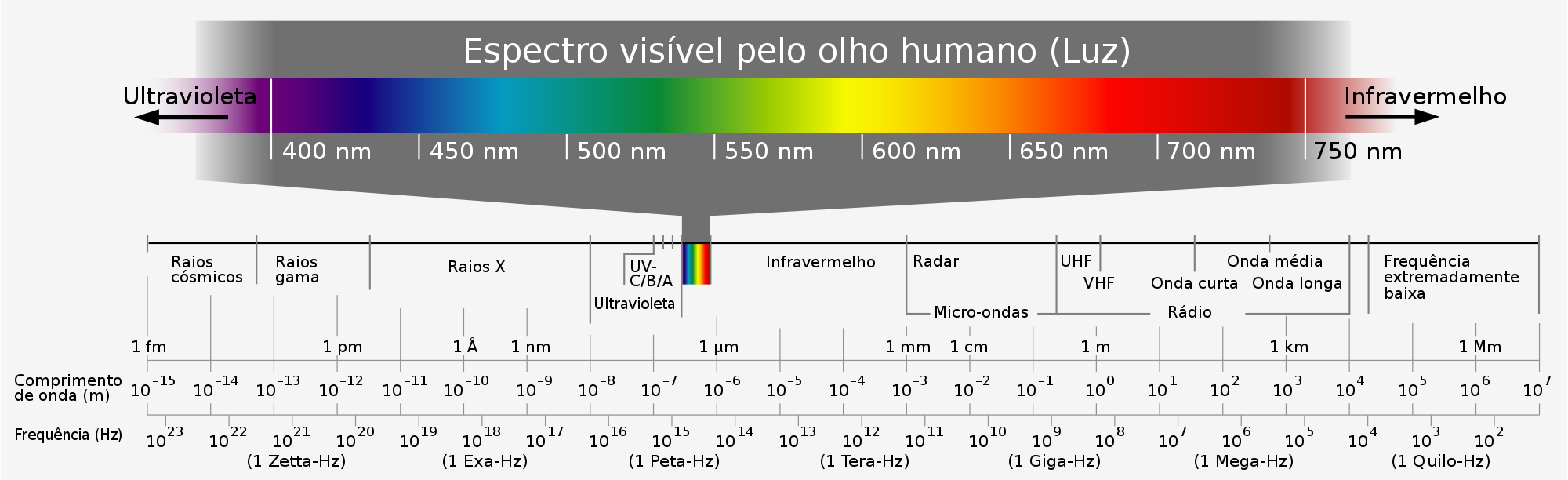
Durante muito tempo o mecanismo de trasferência de calor entre o sol e a terra permaneceu misterioso porque considerava-se impossível a propagação de luz e calor através do vácuo.
Atividade Proposta
Assista o vídeo abaixo e relacione suas dúvidas, conceitos que desconhecia, e suas discordâncias.
Somente em 1900, Planck propôs que a distribuição espectral da potência radiada por um Corpo Negro seria dada por: 1
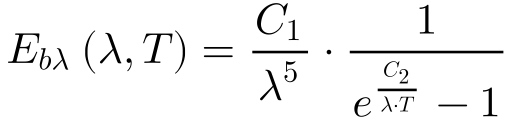
A Equação 2 fornece os coeficientes C1 e C2.
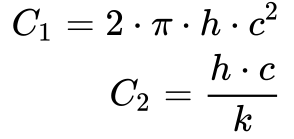
Onde:
-
- Ebλ é a irradiância espectral [W / (m2.μm)];
- h é a constante de Planck [6,626 069 57 e-34 J.s];
- c é a velocidade da luz no meio em questão [ 299 792 458 m/s no vácuo];
- λ é o comprimento de onda da radiação [m];
- T é a temperatura do corpo negro [K];
- k é a constante de Boltzmann [ 1,380 648 8 e-23 J/K];
- C1 e C2 são constantes; 2
- C1= 3,742 e8 [W.μm4/m2 ];
- C2 =1,439 e4 [μm.K]
A Física define Corpo Negro como sendo o material que absorve e/ou emite totalmente a radiação eletromagnética incidente/emitida de/para todas as direções e comprimentos de onda.
De acordo com esta definição, um Corpo Negro jamais poderia ser visto porque não reflete nenhuma luz, a menos que estivesse quente. Este conceito originou a denominação de Buracos Negros.
Por analogia, o Corpo Branco se comporta ao contrário. 3
A Figura 3 apresenta as curvas da irradiância espectral do corpo negro para diversas temperaturas.
A partir da dessa figura, observa-se que:
-
- O espectro da radiação é contínuo com relação à frequência (comprimento de onda);
- O espectro da radiação apresenta um valor máximo que aumenta com o aumento da temperatura;
- A energia emitida aumenta com a temperatura para todas as frequências e, consequentemente, a energia total emitida aumenta com a temperatura;
- O aumento da temperatura do corpo negro desloca a curva para mais altas frequências (menores comprimentos de onda).
A maior temperatura apresentada na figura – 5 800K – corresponde aproximadamente à temperatura na superfície do sol e seu máximo se encontra dentro do espectro da luz visível.
Isto significa que nossos olhos evoluíram para enxergar a luz do nosso sol.
Figura 3. Irradiância Espectral do Corpo Negro
A integral da Equação 1 com relação ao comprimento de onda fornece a potência radiada por área ou fluxo de energia radiada.
A Equação 3, deduzida por Stefan em 1879, fornece o valor dessa integral apesar de Planck somente ter revelado a Equação 1 posteriormente em 1900.
Isto representa mais um exemplo da beleza da evolução da ciência, onde resultados experimentais antecipam descobertas teóricas.
A Equação 4 apenas realça esta beleza, a constante de Stefan-Boltzman se revelou exata e definida a partir de outras constantes fundamentais da física descobertas após a morte Stefan em 1894.
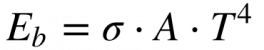
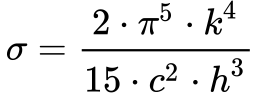
Onde:
-
- Eb é a potência radiada por um corpo negro [W];
- σ é a constante de Stefan-Boltzmann [5,670 374 419 e-8 W/(m2 K4)];
- A é a área [m2];
- T é a temperatura [K];
- k é a constante de Boltzmann [1,380 649 000 00 e-23 (J/Hz)];
- c é a velocidade da luz [2,997 924 58 e8 (m/s)];
- h é a constante de Planck [6.62607015000 e-34 (J/Hz)].
A Equação 5 apresenta a Irradiância Espectral Normalizada com relação à temperatura, também chamada de função corpo negro, que consiste na equação 1 dividida pela temperatura elevada a quinta potência.
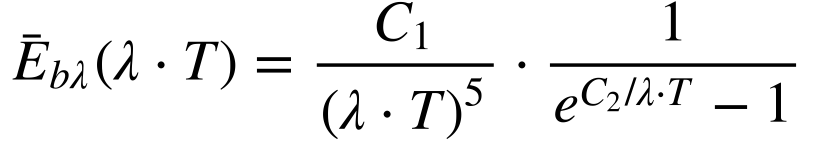
A Figura 4 apresenta o gráfico desta expressão.
Observa-se que a Irradiância Espectral Normalizada independe da temperatura e pode ser utilizada para resolver diversos problemas práticos.
Figura 4. Irradiância Espectral Normalizada
Por exemplo, a Irradiância Espectral Normalizada máxima ocorre sempre com o produto λT igual a 2897,8 μm.K e isto ficou conhecido como a Lei de Wien.
Mais uma vez, esta descoberta experimental se tornou pública antes de Planck revelar a sua equação.
Em decorrência desta lei, corpos sólidos aquecidos começam a emitir luz visível4 quando atingem a temperatura de 798 K (524,85 ºC), chamada de Ponto de Draper.
Esta emissão começa com um tom vermelho escuro e com o aumento da temperatura passa para um tom mais azulado até atingir o “branco quente”.
Esta lei se tornou extremamente útil para realizarmos medições de temperatura razoavelmente precisas utilizando apenas a visão ou equipamentos óticos.
Além disso, um corpo negro no Ponto de Draper emite aproximadamente 23 kW/m2 praticamente toda no infravermelho.
A equação 6 relaciona a frequência com a temperatura no Ponto de Draper.
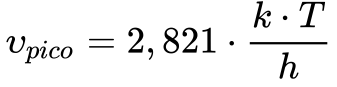
Onde:
-
- v é a frequência [Hz]
- k é a constante de Boltzmann [1,380 648 8 e-23 J/K];
- h é a constante de Planck [6,626 069 57 e-34 J.s];
- T é a temperatura [K].
Problema Proposto
Determine a frequência do ponto de Drapper emitida por seres humanos a 36,5 ºC e a situe no espectro eletromagnético.
Finalmente, precisamos considerar a questão da Emissividade.
Corpos Negro e Branco representam casos limites da realidade.
Na prática, os objetos e materiais emitem e absorvem menos radiação térmica do que o Corpo Negro.
Por isso, a Equação 4 acrescenta um fator multiplicativo, denominado de Emissividade – ε, à Equação 3.
Este fator adimensional se encontra entre 0 e 1 e será abordado posteriormente.
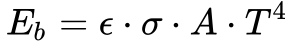
Referências
- CAO, E., Heat Transfer in Process Engineering, McGraw-Hill, 2010
- MAHAN, J.R., Radiation Heat Transfer, John Wiley & Sons, New York, 2002.
- OSTLIE, A. D., CARROL, B., W., Introduction to Modern Stellar Astrophysics, Addison-Wesley, USA, 1996.
- YUNUS, A. C., Heat Transfer – A Practical Approach, 2 edição, McGraw-Hill, 2003.
- INMETRO, Sistema Internacional de Unidades SI, 1ª edição Brasileira do The International System of Units, Rio de Janeiro, 2012, disponível em <http://www.inmetro.gov.br>
- Constantes Físicas
- Espectro Eletromagnético
- https://en.wikipedia.org/wiki/Planck’s_law#References
