Introdução
A Constante Dielétrica ou Permissividade Elétrica Relativa -εr– consiste na capacidade do material de armazenar cargas elétricas e traduz, de forma macroscópica, os efeitos que ocorrem no interior de átomos e moléculas devido ao campo elétrico.
Portanto, ela se encontra diretamente relacionada à estrutura da matéria, e varia em mais de 4 ordens de magnitude dependendo do material.
Nos gases, em decorrência da distância entre moléculas, que resulta em densidades baixas, a constante dielétrica permanece um pouco maior do que a constante dielétrica do vácuo. Por exemplo, a constante dielétrica do ar na pressão de 1 atm vale 1,000 6.
Na maioria das cerâmicas e polímeros, a constante dielétrica varia entre 2 e 10 em decorrência das ligações covalentes.
No caso de materiais com ligações iônicas, a constante dielétrica se encontra entre 6 e 10.
Materiais com elevados valores de constante dielétrica possuem mecanismos especiais de polarização que envolvem a rotação de dipolos ou transformação ferroelétrica de fase.
A água, com constante dielétrica de 80, e o BaTiO3, com constate dielétrica de 1 000, são exemplos desses mecanismos.
Efeitos do Campo Elétrico nos Materiais
A eletricidade surgiu antes da descoberta do elétron e, consequentemente, desenvolveram-se teorias macroscópicas e experimentais para explicar os efeitos do campo elétrico nos materiais.
Posteriormente, passou-se a utilizar as teóricas sobre a estrutura da matéria para explicar o comportamento dos materiais sob campos elétricos.
Comportamento Macroscópico
O Eletromagnetismo explica de forma macroscópica a influência do campo elétrico nos materiais através da criação do vetor de Polarização – P, que reúne macroscopicamente os efeitos do campo elétrico nos materiais de acordo com a Figura 1.
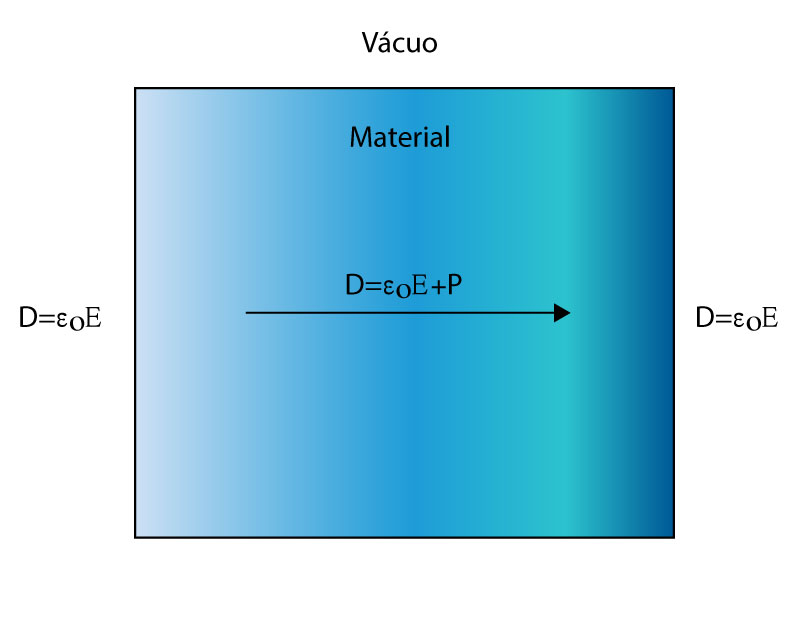
A Equação 1 mostra a relação do vetor P com os vetores densidade de campo elétrico e densidade de fluxo elétrico.
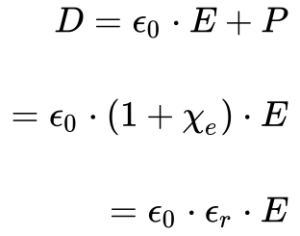
Onde:
- D é o vetor densidade de fluxo elétrico [C/m2];
- E é o vetor densidade de campo elétrico [V/m];
- P é o vetor de polarização elétrica [C/m2];
- ε0 é a permissividade do vácuo [F/m];
- χe é a suscetibilidade elétrica do material;
- εr é a permissividade relativa do material.
A Equação 2 mostra a relação entre o vetor de polarização, o campo elétrico e a propriedade do material expressa em função de uma propriedade macroscópica do material denominada suscetibilidade elétrica.
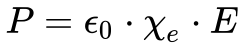
Por sua vez, a Equação 3 apresenta a relação entre as duas outras maneiras de relacionar a susceptibilidade elétrica com a permissibilidade elétrica ou constante dielétrica dos materiais relativa e absoluta.
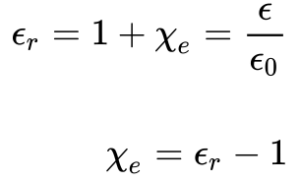
-
- D é a densidade do fluxo elétrico [C/m2];
- P é o vetor de polarização [C/m2];
- E é a intensidade do campo elétrico [V/m];
- ε é a permissividade elétrica ou constante dielétrica do material [F/m];
- ε0 é a permissividade ou constante dielétrica do vácuo [8,854 187 817 81 x 10-12 F/m];
- εr é a permissividade ou constante dielétrica relativa do material;
- χe é a susceptibilidade elétrica do material.
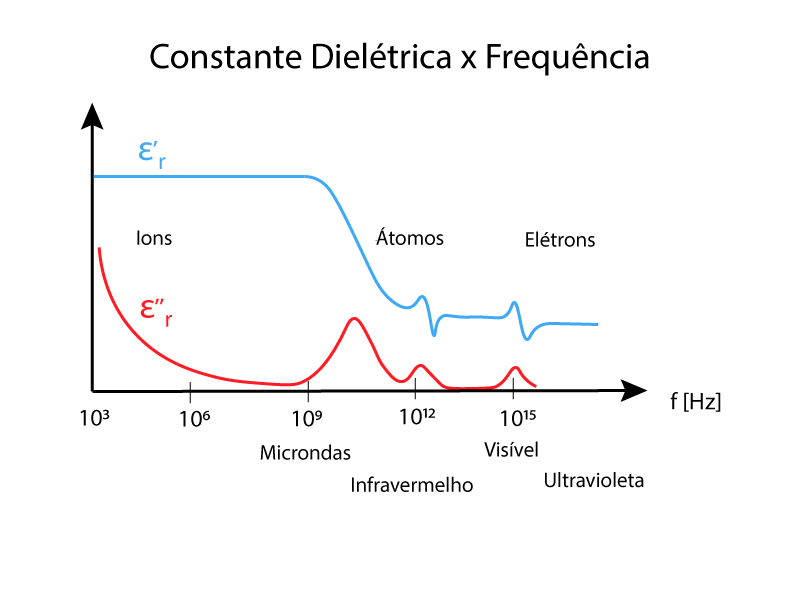
Ela depende da frequência e intensidade do campo elétrico, da temperatura, da pressão e da estrutura do material.
Ao se considerar a frequência do campo elétrico aplicado, a constante dielétrica se torna uma grandeza complexa, possuindo uma parte real e outra imaginária, conforme mostra a Equação 7.
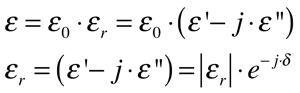
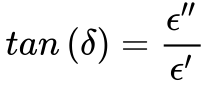
Onde:
-
- ε’ é a parte real da constante dielétrica relativa do material;
- ε” é a parte imaginária da constante dielétrica relativa do material;
- δ é o ângulo de perdas do material;
- tan(δ) é o fator de dissipação do dielétrico;
Exemplo 1 – Comportamento da água
A Figura 2 apresenta a Constante Dielétrica da água em função da frequência e da temperatura.
Figura 2. Constante dielétrica da água.
Observa-se que até 500 MHz, a constante dielétrica da água permanece constante e o fator de dissipação praticamente nulo.
Contudo, a partir dos 500 MHz a componente real começa a decrescer e a imaginária a aumentar independentemente da temperatura.
Além disso, a componente imaginária atinge um valor máximo entre 10 GHz e 30 GHz dependendo da temperatura. Após essas frequências, ambas as componentes decrescem e tendem a zero.
Exemplo 2 – Forno de Micro-ondas
O forno de micro-ondas se tornou a aplicação prática da constante dielétrica mais conhecida na vida moderna.
Capacitores possuem maior utilização porque estão presentes na maioria dos equipamentos elétricos e eletrônicos, mas se encontram invisíveis ao público leigo.
O forno de micro-ondas consiste basicamente numa fonte de ondas eletromagnéticas de frequência fixa (⋍2,4 GHz) que, ao se propagar através dos materiais dielétricos, produz aquecimento.
Todos sabem que não se deve colocar qualquer material no forno de micro-ondas, principalmente condutores.
Além disso, alimentos diferentes se comportam de forma distinta no forno. Como explicar teoricamente este conhecimento empírico?
A Figura 3 mostra uma micro-onda plana incidindo em determinado material homogêneo.
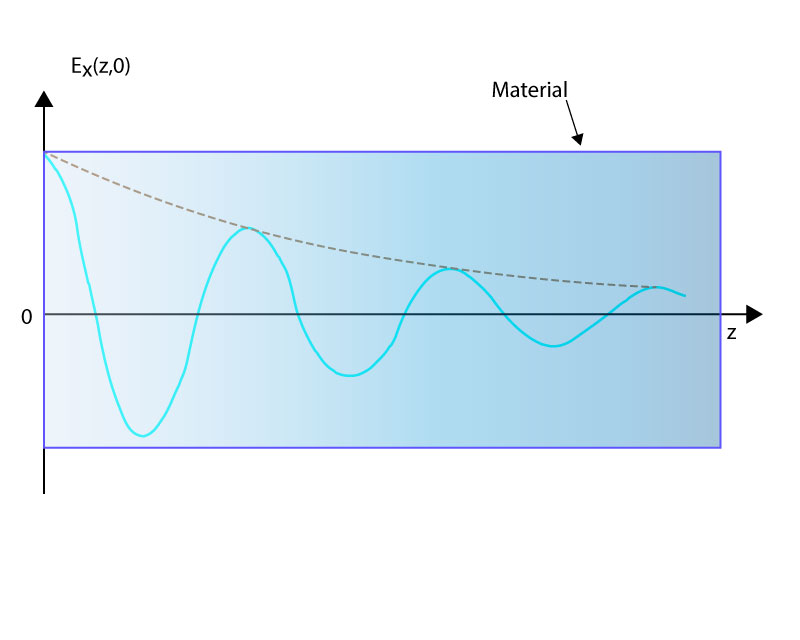
Pode-se descrever o campo elétrico de uma onda eletromagnética plana e uniforme propagando em um material dielétrico homogêneo e isotrópico da seguinte maneira:
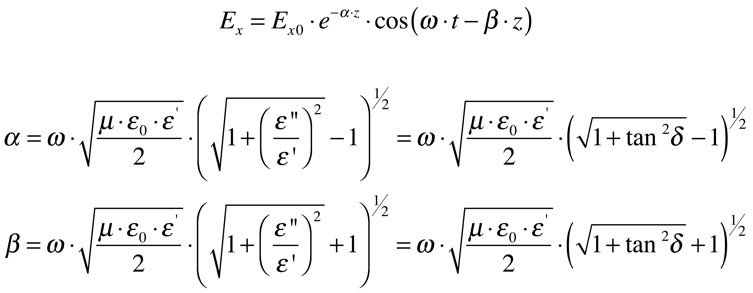
Onde:
-
- α é o coeficiente de atenuação [1/m];
- β é a coeficiente de fase [1/m];
- t é o tempo;
- z é a distância percorrida pela onda no material;
Ao penetrar no material a onda transfere energia para o material e, consequentemente, diminui de amplitude de forma exponencial.
O comprimento de onda – λ – e a impedância intrínseca – η – serão dados por:
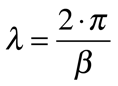
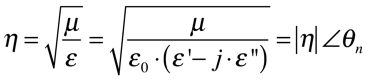
Onde:
-
- λ é o comprimento de onda;
- η é a impedância intrínseca complexa[Ω];
- θn é o ângulo da impedância intrínseca.
A impedância intrínseca representa a impedância do material vista pela onda.
A profundidade de penetração, definida como sendo o inverso da constante de atenuação, representa a distância percorrida pela onda eletromagnética para que a amplitude do campo elétrico diminua 63% (1/e).
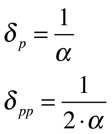
Onde:
-
- δp é a profundidade de penetração da onda;
- δpp é a profundidade de dissipação de potência da onda;1
Isto significa que essa constante mede a capacidade de penetração de determinada onda eletromagnética no material em questão.
A Equação 13 apresenta a densidade de potência dissipada no material em função da impedância intrínseca e do fator de atenuação do material. 2
Neste caso, define-se a profundidade de penetração de potência como sendo a metade da profundidade de penetração do campo elétrico em decorrência do fator 2 no termo exponencial da Equação 13.
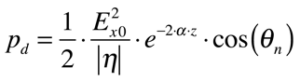
Onde:
-
- pd é a potência por comprimento dissipada no material;
- Exo é a amplitude do campo elétrico da onda ao penetrar no material;
- η é a impedância intrínseca complexa[Ω];
- θn é o ângulo da impedância intrínseca.
- α é o coeficiente de atenuação [1/m].
Isto significa que, dependendo da constante dielétrica do material e da frequência da onda eletromagnética, o aquecimento ocorrerá de forma diferente.
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]kp33ZprO0Ck[/wpdevart_youtube]
As expressões anteriores relativas à constante dielétrica consideraram os materiais isotrópicos.
No caso de materiais anisotrópicos, a constante dielétrica se transforma num tensor de acordo com a equação 14.
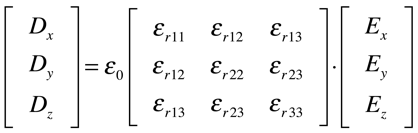
Observa-se que a Densidade de Fluxo Elétrico e a Intensidade de Campo Elétrico são tensores de primeira ordem e, consequentemente, a Constante Dielétrica dos materiais é um tensor de segunda ordem simétrico com as seguintes peculiaridades:
-
- os elementos diagonais são positivos;
- os elementos fora da diagonal podem ser negativos;
- os elementos são números complexos;
- os elementos fora da diagonal possuem módulo menor do que os elementos da diagonal;
- os elementos variam com a frequência do campo elétrico;
- a parte imaginária se encontra associada à perda de energia que ocorre no dielétrico;
- as partes real e imaginária da constante dielétrica podem ter comportamentos e simetrias distintos com a frequência.
A simplificação do tensor constante dielétrica depende da estrutura e da simetria do material. A Tabela abaixo apresenta os diversos tipos de cristais existentes.
Tabela 1. Sistema Cristalinos
| wdt_ID | Sistema | Restrições nas Dimensões | Restrições nos ângulos | Simetria Máxima |
|---|---|---|---|---|
| 1 | Triclínico | nenhuma | nenhuma |  ̄1 |
| 2 | Monoclínico | nenhuma | α=γ=90º | 2/m |
| 3 | Ortorrômbico | Nenhuma | α=β=γ=90º | mmm |
| 4 | Tetragonal | a=b | α=β=γ=90º | 4/mmm |
| 5 | Trigonal | a=b | α=β=90º, γ=120º |  ̄3 |
| 6 | Hexagonal | a=b | α=β=90º, γ=120º | 6/mmm |
| 7 | Cúbico | a=b=c | α=β=γ | m ̄3m |
Materiais Triclínicos
Para este tipo de materiais cristalinos, a Constante Dielétrica se torna um tensor completo conforme a Equação 14.
O Carbonato de Calcio – CaCO3 -, na forma de Aragonita, exemplifica este tipo de material. (ε11=8,67, ε22=8,69, e ε33=8,31 @tamb @ 94GHz)3
Materiais Monoclínicos
Materiais Monoclínicos possuem a constante dielétrica na forma do tensor da Figura 15. Os elementos da diagonal são distintos e apenas dois elementos fora da diagonal são diferentes de zero.
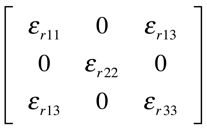
A Gipsita – Ca(SO4).2H2O – exemplifica este tipo de material. (ε11= 5,1, ε22=5,24, ε33= 10,30 @ tamb) 4
Materiais Ortorrômbicos
Materiais Ortorrômbicos apresentam a constante dielétrica na forma do tensor da Figura 16. Os elementos da diagonal são distintos, mas todos os elementos fora da diagonal são nulos.

O Enxofre exemplifica esse tipo de material. (ε11=3,75, ε22=3,95, ε33=4,44) 5
Materiais Uniaxiais
Os materiais uniaxiais representam o conjunto formado pelos cristais Tetragonais, Trigonais e Hexagonais, e possuem a constante dielétrica na forma do tensor apresentado na Figura 17.
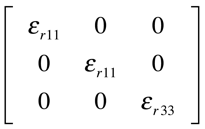
O Titanato de Bário – BaTiO3 – é um exemplo desse tipo de material. (ε11=3600, ε33=150 sem pressão mecânica @ 100 KHz, e ε11=2300, ε33=80 com pressão mecânica @ 250MHz, todos @ 298 K) 6
Materiais Cúbicos
Finalmente, os materiais com cristais cúbicos possuem apenas os elementos diagonais e são todos iguais. Isto significa que a notação tensorial não se torna necessária com esses materiais.
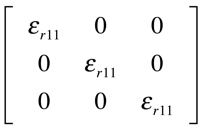
O óxido de cobre -CuO- exemplifica esse tipo de material (ε =18,1 @ tamb 2MHz) 7
Tabela 2. Propriedades Dielétricas
Fonte: Matweb
Material Símbolo Rigidez Dielétrica[kV/mm] Constante Dielétrica Relativa Observações Fator de dissipação
Bromo Br 3,15
Selênio Se 6,60
Alumina Al2O3 9,00 9,3
Quartzo SiO2 4,2
Baquelite Sumitomo Durez 22257 7,9 5,5 @ 1 MHz 0,08
Germanium Ge 16
Silício Si 11,8
Estanho Sn 24
Metanol 32,63
Etanol 24,3
PPA com fibra de vidro 0.8 a 37,0 3,59 a 136 varia com a frequência e temperatura 0,005 a 0,85
Água H2O 55,51 a 87,9
80.2 @20Cvaria com a temperatura e pressão
Água Pesada D2O 78,06 @ 20C
Titanato de Bario BaTiO3 1000 a 5000
Modelo Equivalente
Para analisar circuitos elétricos com materiais dielétricos, pode-se utilizar as seguintes expressões:
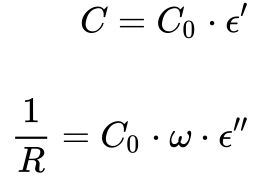
Onde:
-
- C é a capacitância equivalente;
- C0 é a capacitância sem o material dielétrico;
- R é a resistência equivalente em paralelo com o capacitor;
- ε’ é a parte real da constante dielétrica relativa do material;
- ε” é a parte imaginária da constante dielétrica relativa do material;
- ω é a frequência da tensão/corrente aplicada no material.
Exemplo 3 – Material dielétrico entre duas placas paralelas
Por exemplo, considerando um material dielétrico capacitor de placas paralelas, conforme mostra a Figura 4, C0 possuirá o valor apresentado na Equação 20.8
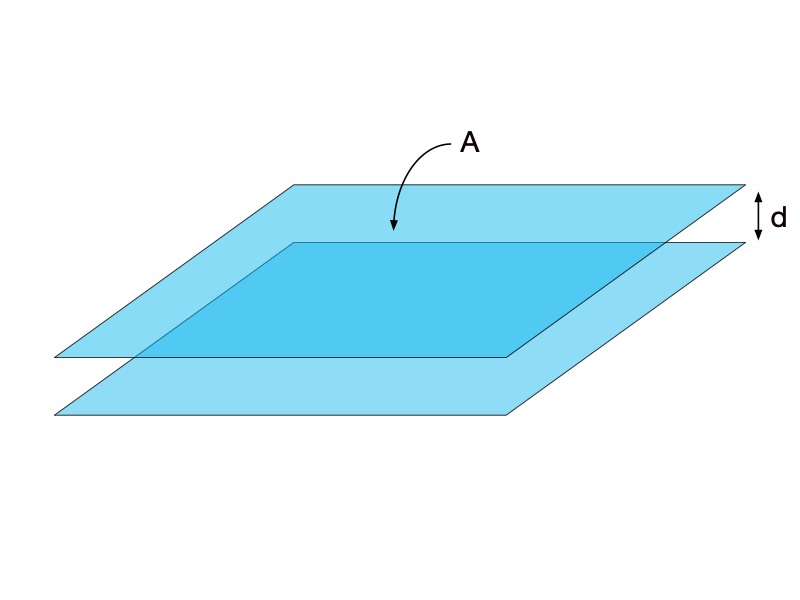
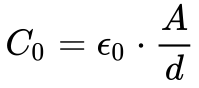
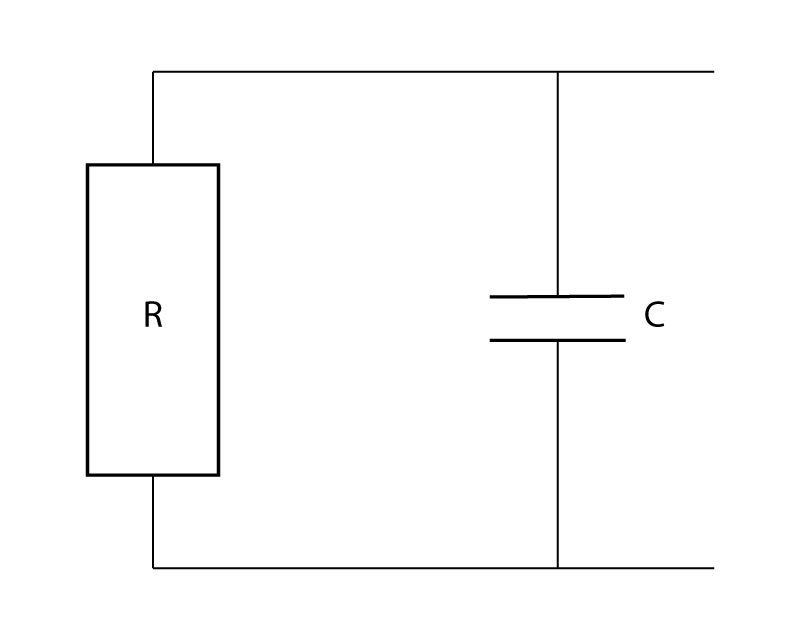
A Figura 5 apresenta o circuito equivalente de materiais dielétricos submetidos a campos elétricos.
É importante observar que este modelo se mantém válido para qualquer geometria porque o efeito da geometria se encontra no cálculo de C0.
Referências
- AGILENT TECHNOLOGIES, Basics of Measuring the Dielectrics Properties of Materials – Application Note,
- HAYNES, W.M., LIDE, D. R., BRUNO, T. J., (editors) Handbook of Chemistry and Physics, CRC Press, 93 ed., 2013.
- KAO, K.C., Dielectric Phenomena in Solids, Elsevier, 2004.
- NOTAROS, B. M., Eletromagnetismo, Pearson, 2012. 9
- PEEK, F. W., Dielectric Phenomena in High Voltage Engineering, McGraw-Hill, 2 ed., 1920.
- RAJU, G. G., Dielectrics in Electric Fields, Dekker, 2002.
- SOLYMAR, L., WALSH, D., SYMS, R. R. A., Electrical Properties of Materials, Oxford, 10 ed., 2019. 10
- VON HIPPEL, A. R., Dielectrics and Waves, MIT, 1954.
