As turbinas hidráulicas, classificadas como turbinas de fluidos incompressíveis para diferenciar das turbinas a gás e a vapor, transformam a energia potencial da água armazenada nos reservatórios em energia mecânica.
Introdução
As primeiras turbinas hidráulicas surgiram com os gregos e romanos na antiguidade. No entanto, as máquinas modernas surgiram no século XIX com o desenvolvimento da hidrodinâmica e a partir dos projetos do professor francês Claude Burdin[1].
As turbinas podem ser classificadas de acordo com a Tabela abaixo.
Tipos de Turbinas Hidráulicas
Tipo Radial Axial Mista Mista
Diagonal Tangencial
Ação Francis Kaplan
BulboFrancis
Reação Pelton
Nas turbinas axiais, a água flui paralelamente ao eixo de rotação, e a turbina Kaplan pertence a este tipo. Por outro lado, nas turbinas radiais, a água escoa perpendicularmente ao eixo de rotação, e a turbina Francis exemplifica esta classe. Finalmente, nas turbinas de impulso a água escoa tangencialmente à turbina e perpendicularmente ao eixo de rotação, e a turbina Pelton pertence a este tipo.
A Figura 1 apresenta os principais tipos de turbina hidráulicas utilizadas na geração de energia com as respectivas faixas operativas. Observa-se que as turbinas Kaplan se destinam a usinas com quedas entre 1 e 100 m, as Pelton para usinas com quedas superiores a 100m com vazões inferiores a 60 m/s, e as turbinas Francis para usinas com quedas entre 10 e 700 m e vazões entre 1 e 900 m/s.
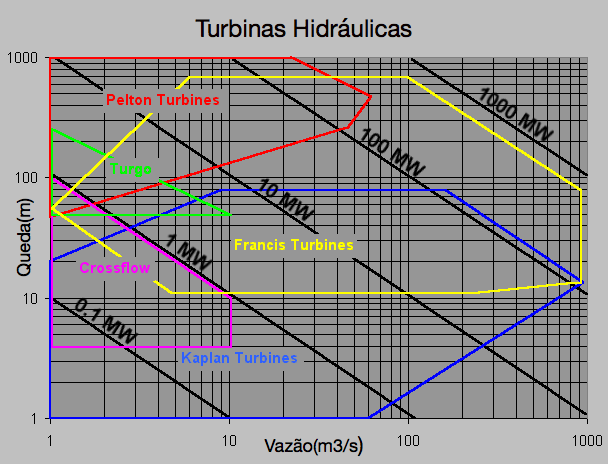
Em decorrência dessas características, existem apenas três usinas (1,6%) operando com Turbinas Pelton no Brasil.1 Por outro lado, existem 70 usinas utilizando Turbinas Kaplan (38%) e 111 com Turbinas Francis (60%). Torna-se importante ressaltar que as turbinas Francis fornecem as maiores potências e o atual limite máximo de 700 MW encontra-se em Itaipu.
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]k0BLOKEZ3KU[/wpdevart_youtube]
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]AT7B7IWmOtU[/wpdevart_youtube]
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]3BCiFeykRzo[/wpdevart_youtube]
O capítulo de Hidrelétricas mostrou que a energia disponível numa usina hidrelétrica depende da energia potencial da água armazenada, que se transforma em energia cinética ao longo da tubulação até a entrada da turbina. Por sua vez, a energia cinética na entrada da turbina se converte parcialmente em energia cinética no eixo da turbina. As turbinas hidráulicas possuem elevada eficiência, mas, como manipulam enormes quantidades de energia, pequenas perdas de representam grandes quantidades de energia. Por isso, existe uma constante preocupação com o aumento do rendimento.
A Figura 2 apresenta a variação do rendimento da turbina hidráulica em função da velocidade de rotação. A turbina parada não produz energia e, consequentemente, possui rendimento nulo. Conforme a turbina adquire velocidade, sua potência aumenta até atingir um valor máximo. A partir desse ponto, a turbina passa a gerar menos potência até atingir novamente um ponto de rendimento zero. 2
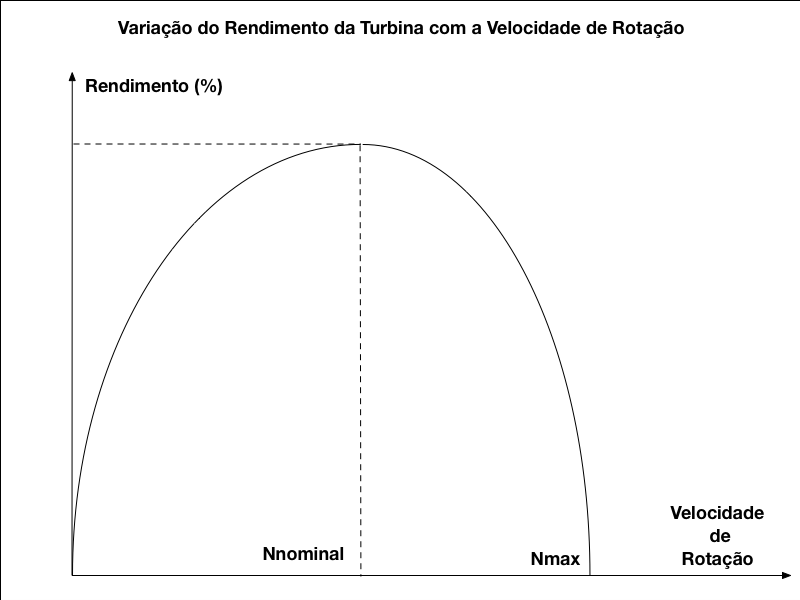
Observa-se que o rendimento máximo se encontra associado a uma determinada velocidade e, por isso, escolhe-se esta velocidade como a velocidade nominal da turbina.
Além disso, o rendimento da turbina passa a diminuir após atingir seu valor máximo até atingir zero quando a turbina atinge sua velocidade máxima.
Este evento ocorre quando a potência elétrica se anula repentinamente. Por exemplo, isso ocorre no caso de atuação quando o sistema de proteção desconecta usina da rede. Neste caso, a potência elétrica cai instantaneamente a zero, mas a potência mecânica permanece constante. Denomina-se este evento de rejeição total de carga e a velocidade máxima de velocidade de disparo. A existência desta velocidade limite possui um papel extremamente importante de proteção para os equipamentos.
Nos casos de rejeição de carga, as máquinas começam a acelerar e o sistema de controle de frequência deve atuar para reduzir a velocidade da máquina para valores seguros.
A Figura 3 mostra o sistema de controle das usinas geradoras de energia elétrica.
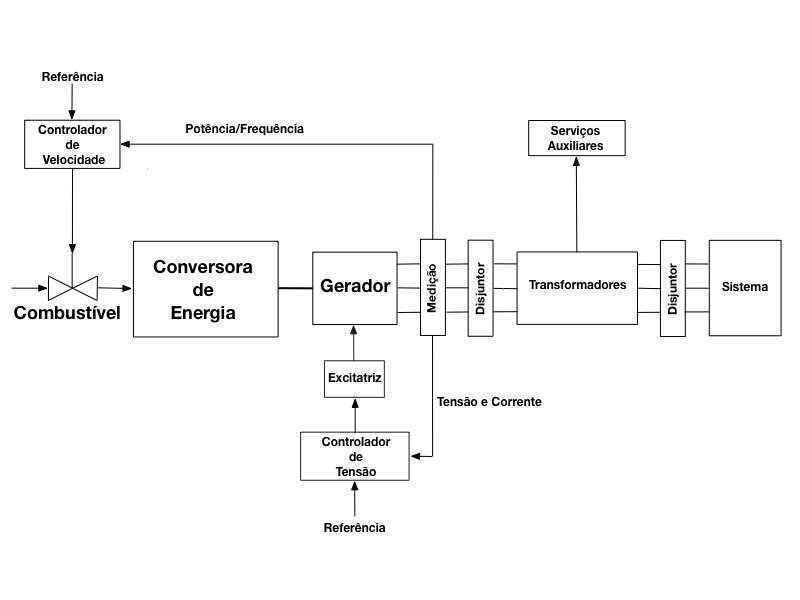
A malha de controle de frequência/potência controla a quantidade de combustível fornecida para a máquina térmica ou hidráulica utilizada.
Características das Turbinas Hidráulicas
O objetivo do projeto da Turbina Hidráulica consiste em obter o rendimento máximo nas condições de vazão(Q), queda(H) e velocidade de rotação(N) nominais.
A Equação 1, obtida a partir da Equação 7 do Capítulo Hidrelétricas, fornece o valor do rendimento da turbina nessas condições.
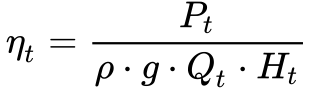
Onde:
-
- Pt é a potência mecânica no eixo da turbina[kW];
- ηt é o rendimento mecânico da turbina;
- Qt é a vazão na entrada da turbina[m3/s];
- Ht é a queda líquida na turbina[m];
- ⍴ é a densidade da água[kg/m3];
- g é a aceleração da gravidade [m3/s].
Obtém-se as curvas características das turbinas hidráulicas, incluindo seu rendimento, experimentalmente porque não existem fórmulas teóricas.
Controla-se a vazão nas turbinas através da abertura das válvulas de controle e a Figura 4 apresenta a variação do rendimento em função da abertura (vazão) e da velocidade.
Observa-se que o ponto de máximo rendimento varia com a vazão e com a velocidade de rotação. Como as turbinas operam com velocidade constante para manter a frequência da tensão gerada, o rendimento da usina diminui quando as turbinas operam fora da vazão e da altura nominais.
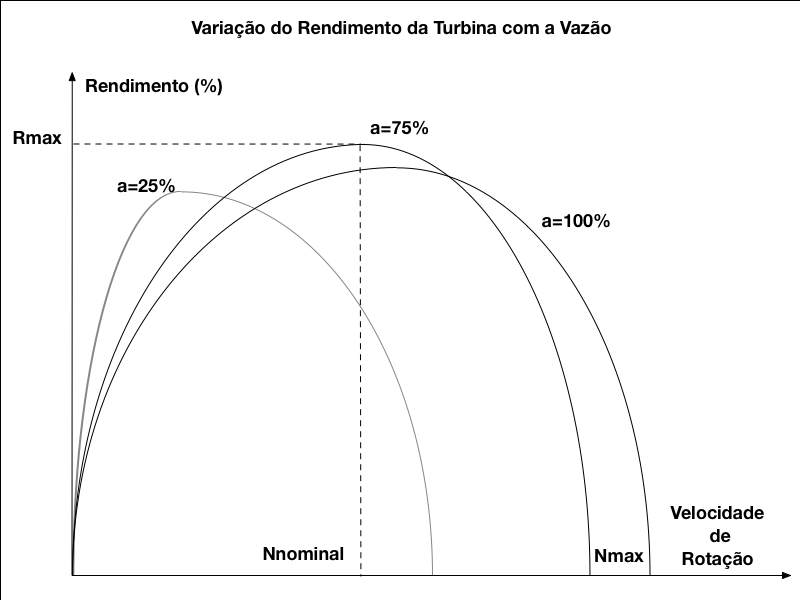
Portanto, cada curva deve ser determinada experimentalmente e, para reduzir o custo de desenvolvimento, utiliza-se modelos reduzidos nessas medições.
Análise Dimensional de Turbinas Hidráulicas
O objetivo do projeto das turbinas hidráulicas consiste em obter o máximo de energia a partir de determinada vazão Q, altura H e velocidade de rotação N. Por isso, torna-se fundamental conhecer do rendimento em função desses parâmetros.
Para isso, a engenharia utiliza a técnica de modelos em escala reduzida porque torna-se muito mais econômico construir modelos reduzidos de máquinas e ensaiá-las antes de construir as máquinas reais. Além disso, torna-se impossível ensaiar turbinas hidráulicas reais porque inexistem as quedas e fluxos de água necessários em laboratórios.
Contudo, para que a simulação retrate a realidade, os modelos devem se comportar da mesma maneira que os equipamentos reais, isto é, devem ser geometricamente e dinamicamente semelhantes.
Obtém-se a semelhança geométrica através da manutenção das relações de comprimento e ângulos.
Adicionalmente, a semelhança dinâmica requer velocidades semelhantes nos diversos pontos da máquina.
Porém, é impossível satisfazer simultaneamente essas duas condições mantendo os efeitos da viscosidade do fluido semelhante. Isto significa que as condições da água no modelo diferem um pouco das condições do fluido na máquina real, isto significa diferentes números de Reynolds. Contudo, este efeito se torna desprezível na maioria dos casos.
A Tabela abaixo apresenta as variáveis extensivas de interesse no projeto de turbo máquinas.
Grandezas Hidráulicas
| wdt_ID | Grandeza | Símbolo | Dimensões | Unidades |
|---|---|---|---|---|
| 1 | Fluxo | Q | L3/t | m3/s |
| 2 | Energia Específica | E | L2/t2 | m2/s2 |
| 3 | Potência | P | ML2/t3 | m2/s2 |
| 4 | Velocidade de rotação | N | 1/t | 1/s |
| 5 | Dimensão | D | L | m |
| 6 | Densidade | ⍴ | ML/t3 | kg/m3 |
| 7 | Viscosidade | μ | M/l/t | kg/m/s |
A aplicação dos conceitos de similaridade levou a utilizar às seguintes variáveis intensivas e adimensionais.
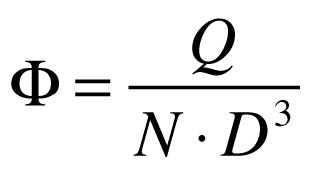
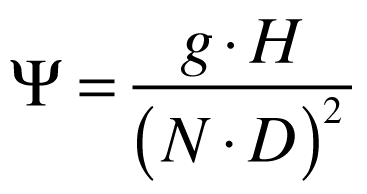
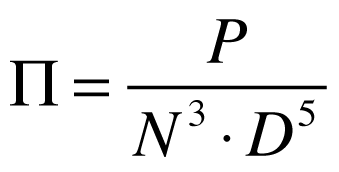
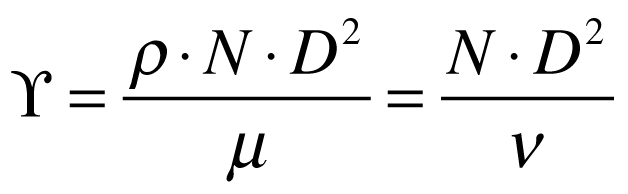
Onde:
-
- Φ é o coeficiente de fluxo;
- Ψ é o coeficiente de altura;
- Π é o coeficiente de potência;
- Υ é o coeficiente diâmetro;
- Q é a vazão;
- N é a velocidade de rotação;
- D é o diâmetro ou dimensão linear;
- H é a queda;
- g é a aceleração da gravidade;
- P é a potência mecânica;
- ⍴ é a densidade da água;
- μ é a viscosidade dinâmica;
- ν é a viscosidade cinemática
Similaridade
A comparação de turbinas iguais ou geometricamente semelhantes só pode ser feita quando existe similaridade geométrica e hidrodinâmica.
Quando isto ocorre, podemos dizer que o rendimento mecânico é igual e as seguintes relações, obtidas a partir da manutenção dos coeficientes acima, devem existir.
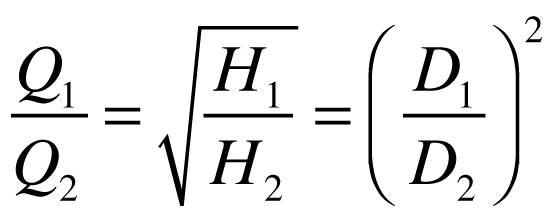
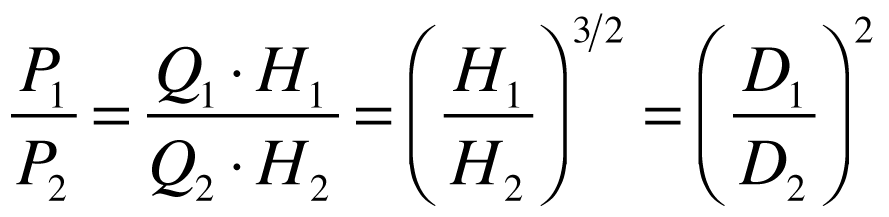
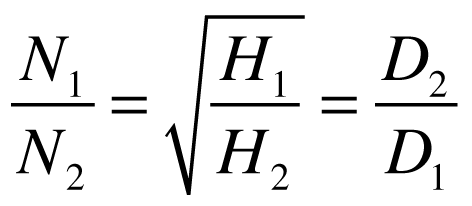
Velocidade Específica
Combinando os coeficientes de queda e potência de modo a eliminar D, obtemos a seguinte grandeza adimensional chamada de velocidade específica.
Referências
- ROUND, G.F., Incompressible Flow TurboMachines – Design, Selection, Applications, and Theory, Elsevier, 2004.
- MACINTYRE, A. J., Máquinas Motrizes Hidráulicas, Guanabara Dois, 1983. 3
- DIXON, S. L., HALL, C.A., Fluid Mechanics and Thermodynamics of Turbomachinery, Elsevier, 6 edição, 2010.
- BETZ, A., Introduction to the Theory of Flow Machines, Pergamon Press, 1966.
- SAYERS, A.T., Hydraulic and compressible flow turbomachines, McGraw-Hill, 1990.
