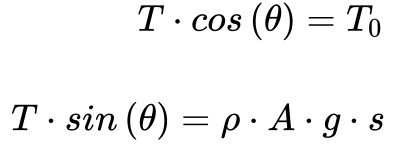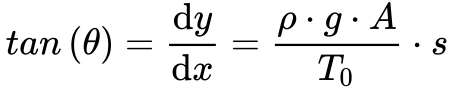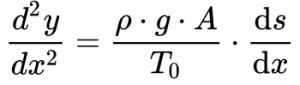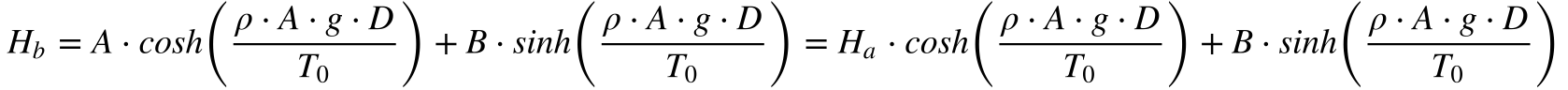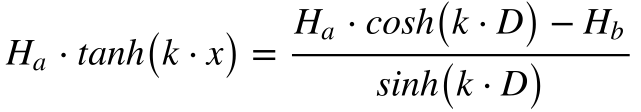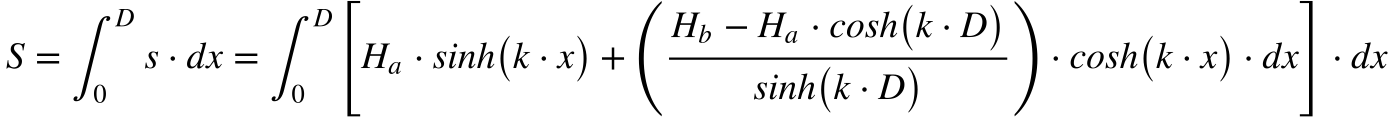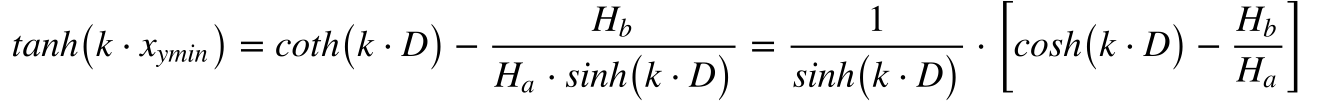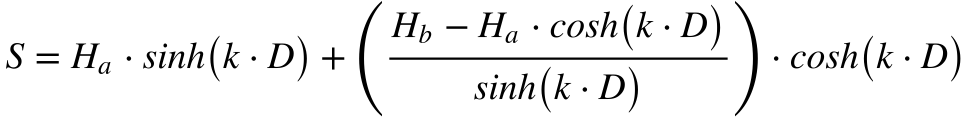-
- Peso do cabo;
- Comprimento do cabo;
- Material do cabo;
- Temperatura do cabo;
- Distância entre as torres;
- Altura das torres;
- Tração no cabo.
Quem fez o trabalho de cabos, encontrou uma expressão do segundo grau para aproximar os pontos medidos. Contudo, como podemos obter a equação do cabo utilizando a física e a matemática?
Fórmula da Catenária
Este problema matemático foi proposto por Jacob Bernoulli em 1690, mas anteriormente Galileu Galilei havia sugerido que a curva seria uma parábola. Portanto, fiquem felizes se os resultados obtidos por vocês neste trabalho foram equações de segundo grau, vocês chegaram ao mesmo resultado que Galileu.
Contudo, somente em 1691 Johan Bernoulli, irmão de Jacob Bernoulli, apresentou a solução para este problema. Na época, esta demonstração representou enorme avanço matemático, mas hoje não passa de um exercício de cálculo do ciclo básico.
Considerando a referência dos eixos no ponto central do cabo e analisando o equilíbrio de estático de forças da Figura 1, teremos que a componente horizontal de T deverá ser sempre igual a To, e a componente vertical deverá igualar ao peso do segmento do cabo.
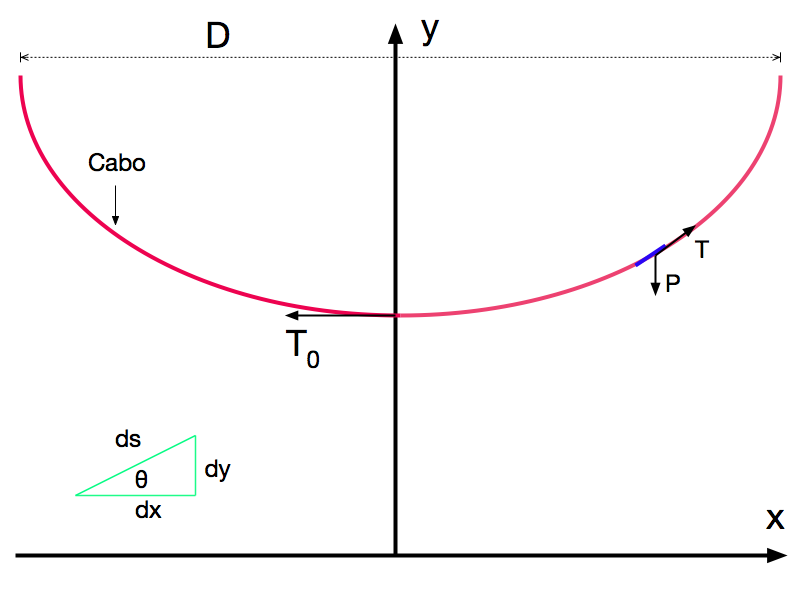
-
- T é a tensão no cabo[N];
- θ é o ângulo do cabo no ponto com relação aos eixos de referência;
- T 0 é a tensão horizontal no cabo na origem dos eixos [N];
- ρ é a massa específica do cabo [kg/m3];
- A é a área da seção reta do cabo[m2];
- g é a aceleração da gravidade[m/s2];
- s é o comprimento infinitesimal do cabo[m].
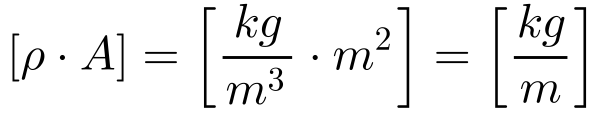
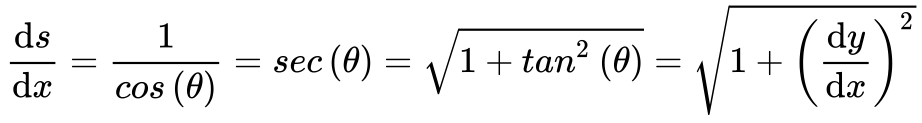
Substituindo a Equação 4 na Equação 3, obtemos a seguinte relação:
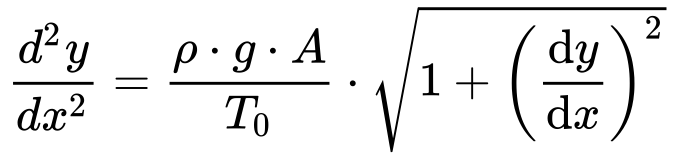
Como resolver esta equação diferencial?
A dica consiste em usar o artifício da substituição de variáveis.
Cria-se uma variável z, conforme a expressão abaixo, e substituindo na equação (4), teremos que:
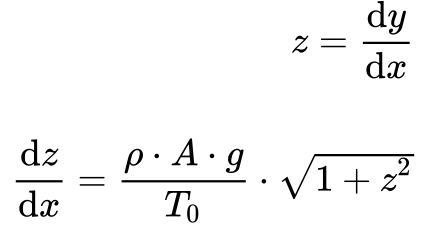
Rearrumando a equação 6, obtemos que:
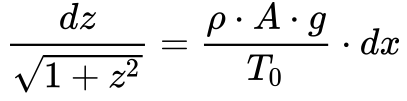
A solução da Equação 7 requer que os dois termos da expressão sejam iguais a uma constate. Consequentemente, integrando os dois termos teremos que:1
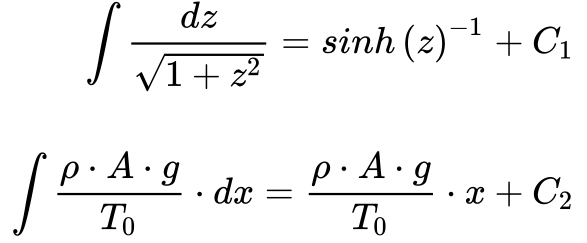
As constantes C1 e C2 dependem das condições iniciais do problema. Neste caso específico, de acordo com a Figura 1, as constantes C1 e C2 são iguais e a solução se torna:
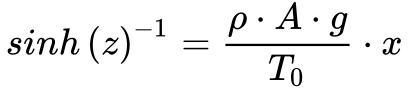
A Equação 10 fornece o valor de z a partir da Equação 9.
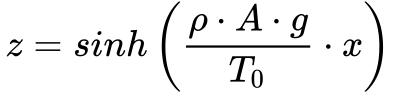
A partir das Equações 6 e 2, pode-se escrever que:
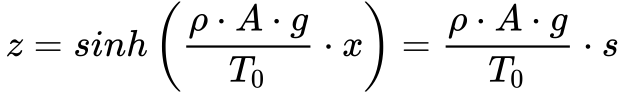
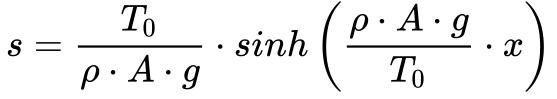
Levando em consideração a simetria da Figura 1, o comprimento total do cabo – S – será dado por:
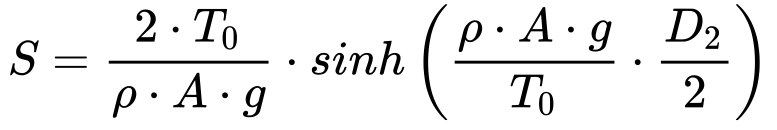
A constante abaixo possui dimensão de comprimento e representa a força de tração horizontal dividida pelo peso do cabo por unidade de comprimento.
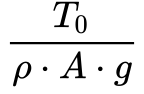
Para distâncias entre torres menores que esta constante, o cabo fica praticamente esticado e sem barriga. Por outro lado, para distâncias entre torres maiores, a barriga aumenta.
Obtém-se a altura do cabo a partir da Equação 15.
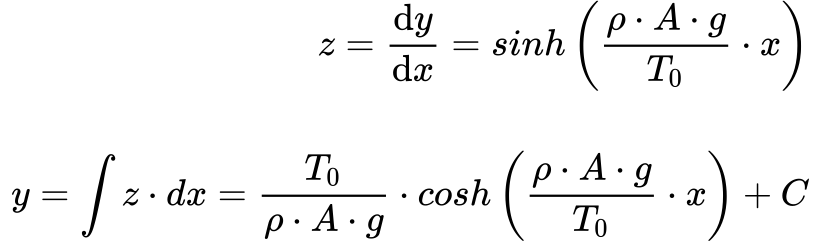
A constante C depende das condições de contorno do problema específico. No caso em questão e de acordo com a Figura 1, como y=0 pra x=0, a constante C será dada por:
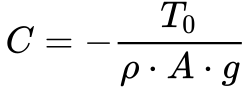
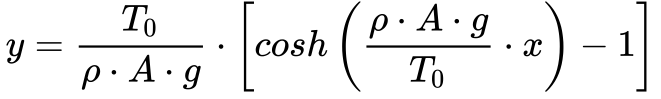
A Flexa máxima, que corresponde à altura da torre – Ht – menos a distância ymax , que se calcula pela Equação 18.
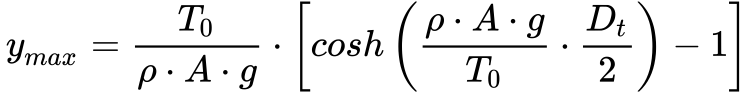
No caso geral de alturas de torre diferentes, mostrado na Figura 2, a altura da linha será dada pela equação 19.
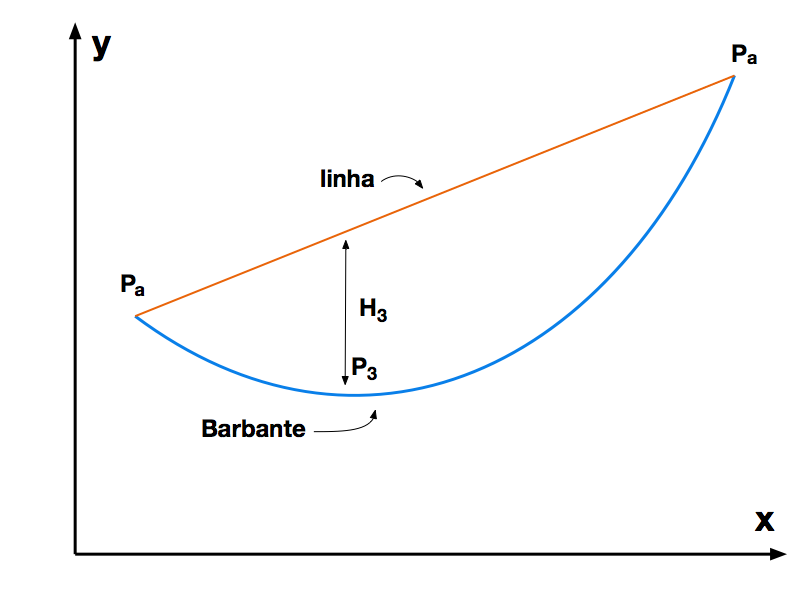
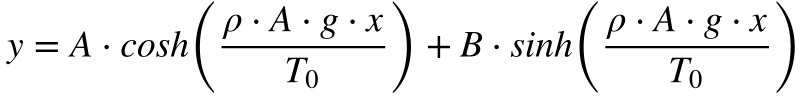
Considerando a altura da linha igual Ha para x=0 e Hb para x=D (distância entre as torres), teremos que:
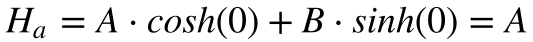
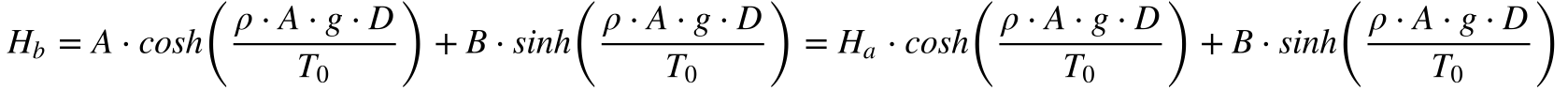
Substituindo o valor de A, obtido pela Equação 20, na equação 21, obtém-se o valor de B.
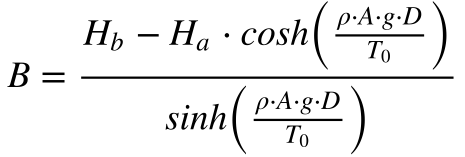
Desta maneira, a equação 23 fornece a altura do cabo em função de x e dos parâmetros da linha.
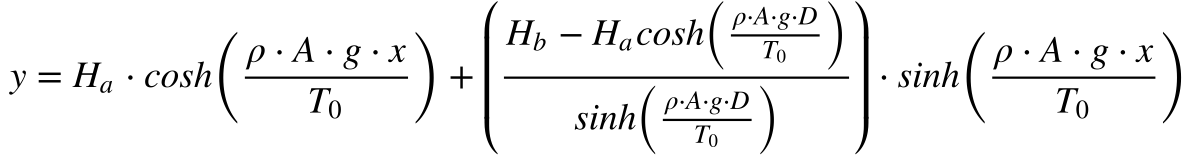
A altura mínima da linha ocorrerá quando a derivada da altura em relação à distância for igual a zero. Desta maneira, teremos que: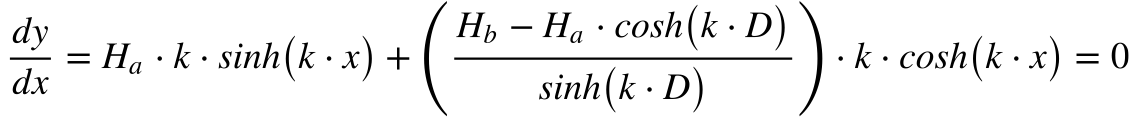
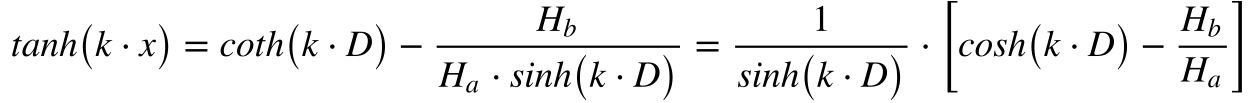
Onde:
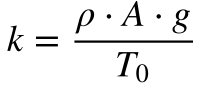
Conforme visto no início, a derivada do comprimento do cabo será dada por:
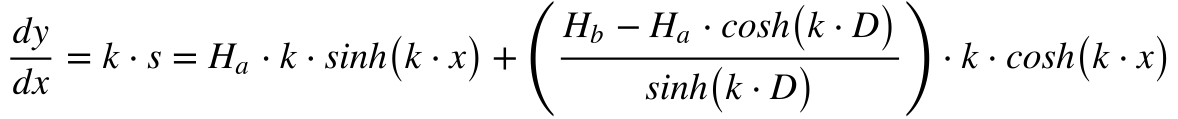
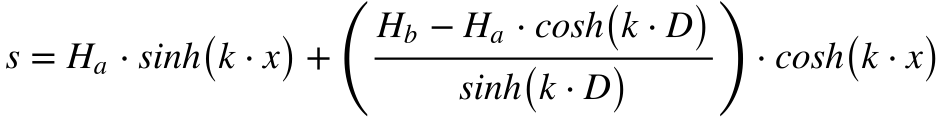 O comprimento total do cabo será dado por:
O comprimento total do cabo será dado por:
Finalmente, assistam a este vídeo que conta tudo isso de forma muito interessante.
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]JlL6ZHChhQE[/wpdevart_youtube]
[wpdevart_youtube width=”640″ height=”385″ autoplay=”0″ theme=”dark” loop_video=”0″ enable_fullscreen=”1″ show_related=”1″ show_popup=”0″ thumb_popup_width=”213″ thumb_popup_height=”128″ show_title=”1″ show_youtube_icon=”1″ show_annotations=”1″ show_progress_bar_color=”white” autohide_parameters=”1″ set_initial_volume=”true” initial_volume=”72″ disable_keyboard=”1″]CP3fMa9iq8w[/wpdevart_youtube]