As sete células primitivas apresentadas anteriormente permitem elementos físicos 1apenas nos seus vértices.
Contudo, será a menor célula unitária sempre a melhor célula?
Ou, será possível escolher uma célula unitária maior.
A escolha da Célula unitária deve levar em consideração os seguintes aspectos:
-
- Deve ser a menor possível, isto significa que deve possuir o menor volume;
- Deve respeitar a simetria da rede cristalina, isto é, os lados da célula devem estar paralelos aos eixos de simetria ou perpendiculares aos planos de simetria;
- Os eixos da célula devem ser ortogonais ou hexagonais sempre que possível;
O papel de parede serve como exemplo para explicar os conceitos de Cristalografia. Inicialmente, observa-se que existem duas figuras distintas que se repetem, uma maior envolta por um círculo e outra menor com quatro pontos. Essas duas figuras podem representar átomos, moléculas, ou grupos quaisquer de materiais.
A Figura 1 apresenta quatro possibilidades2 de células – preta, vermelha, verde e azul – e quatro eixos de simetria – linhas pontilhadas.
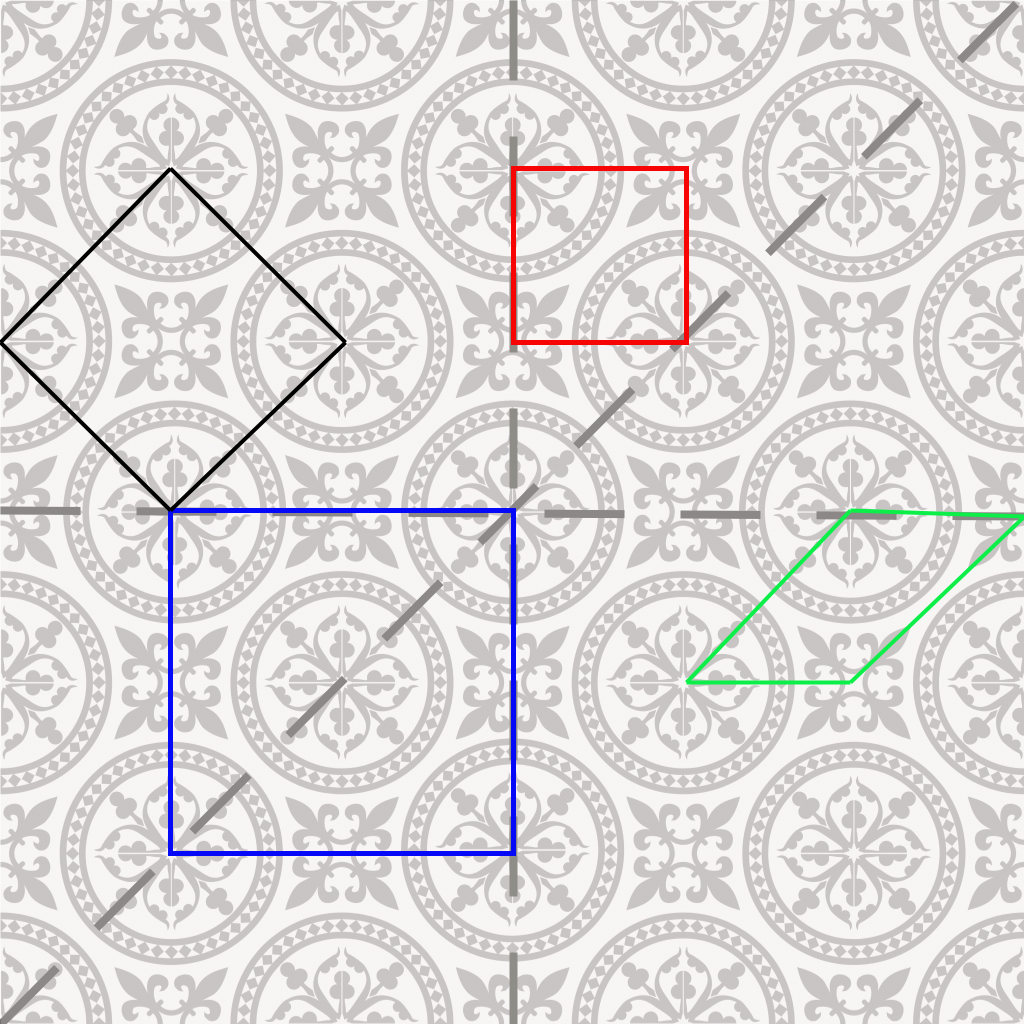
A célula vermelha possui a menor área – a2 3 , é ortogonal, mas viola a condição de poder completar a figura apenas com translação sem deixar espaços vazios.
A célula verde também possui área igual- a2, mas não completa a figura com movimentos de translação, e não é ortogonal nem hexagonal.
A célula preta possui área duas vezes maior- 2a2, completa a figura com movimentos de translação diagonais, é ortogonal, mas exige a existência de um elemento adicional no cento da figura, que não existe nas células primitivas anteriores.
Finalmente, a célula azul possui a maior área – 4a2, completa a figura com movimentos de translação, é ortogonal, mas também exige a existência de um elemento adicional no cento da figura.
A Figura 2 apresenta as quatro possibilidades de incorporar elementos nas células primitivas fora dos vértices. Portanto, como existem sete (7) células primitivas e quatro(4) novas possibilidades, teríamos um total de vinte e oito (28) estruturas cristalinas possíveis.
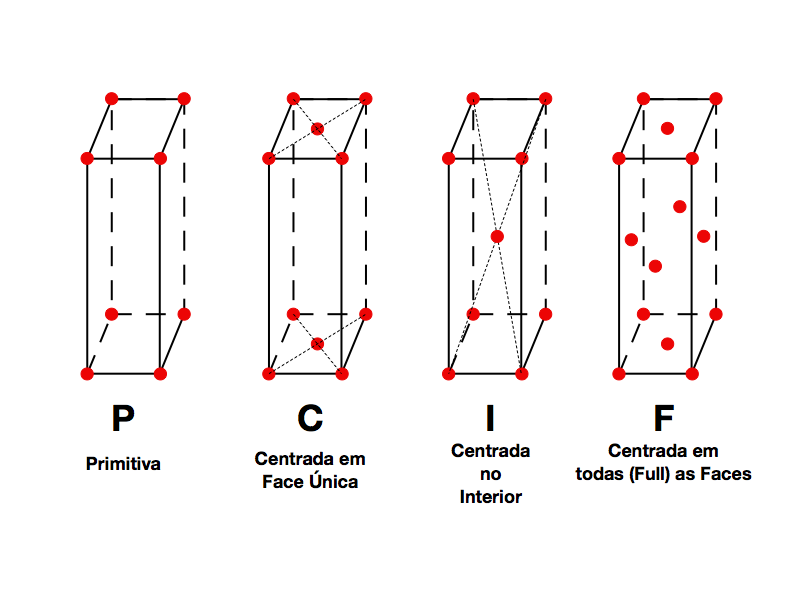
Contudo, Auguste Bravais demonstrou em 1848 que existiam apenas catorze (14) redes cristalinas únicas e diferentes no espaço tridimensional, que passaram a ser denominadas de Redes de Bravais, conforme mostra a Tabela 2.
Tabela 2. Rede de Bravais
wdt_ID Sistema Primitivo - P Centrado em Face Única - C Centrado no Interior - I Centrado em Todas as Faces - F
1
Triclínico
Sim
Não
Não
Não
2
Monoclínico
Sim
Sim
Não
Não
3
Ortorrômbico
Sim
Sim
Sim
Sim
4
Tetragonal
Sim
Não
Sim
Não
5
Trigonal
Sim
Não
?
Não
6
Hexagonal
Sim
Não
Não
Não
7
Cúbico
Sim
Não
Sim
Sim
