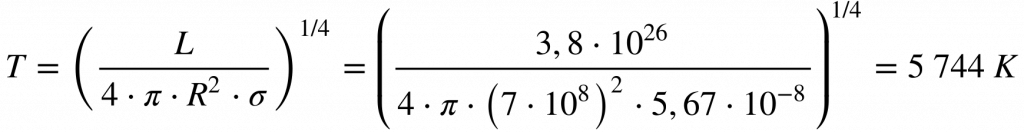Energia Solar

 

“A fonte de todas as energias é o sol. O grande desafio consiste em como usar toda essa energia.”

George P Shultz

O sol fornece a energia primária da terra, e as energias solar, eólica, biomassa e hidrelétrica dependem dele.

Até mesmo as fontes fósseis se originam do sol porque resultam da decomposição de material orgânico, por ele criado.

Apenas as energias geotérmica e nuclear independem do sol, apesar do núcleo da terra e do urânio terem sido criados em alguma estrela. 

Existem duas tecnologias atualmente disponíveis para o aproveitamento da energia solar: a Fotovoltaica e a Termossolar.

A Termossolar transforma a energia do sol em eletricidade utilizando máquinas térmicas operando com ciclo Rankine.

A Fotovoltaica converte a luz diretamente em eletricidade através de semicondutores utilizando o efeito fotoelétrico. Portanto, a geração Fotovoltaica constitui a primeira conversão de energia totalmente elétrica e baseada na Mecânica Quântica.

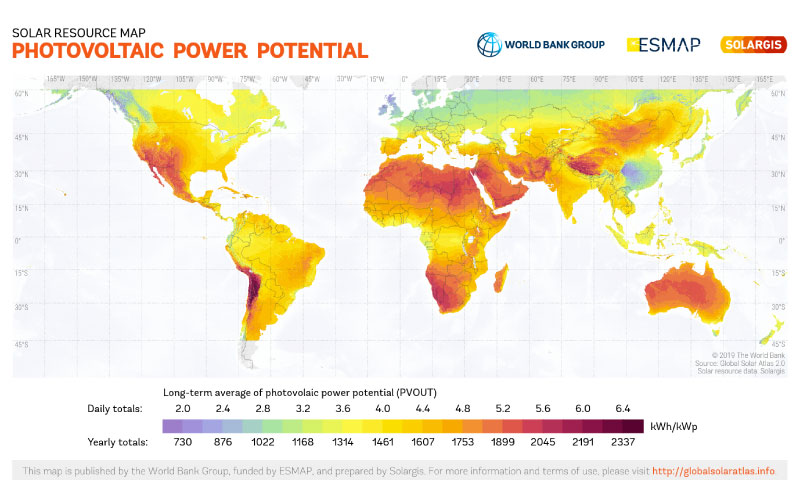
A Figura 1 apresenta o potencial de geração Fotovoltaica mundial.

Observa-se que o Brasil não apresenta os índices mais elevados apesar de ser um país tropical e quente, mas possui um potencial que deve ser aproveitado.

Adicionalmente, observa-se que as regiões próximas à linha do Equador não apresentam o maior potencial fotovoltaico devido à influência das nuvens e da chuva, mas as regiões mais áridas e elevadas possuem os maiores potenciais.

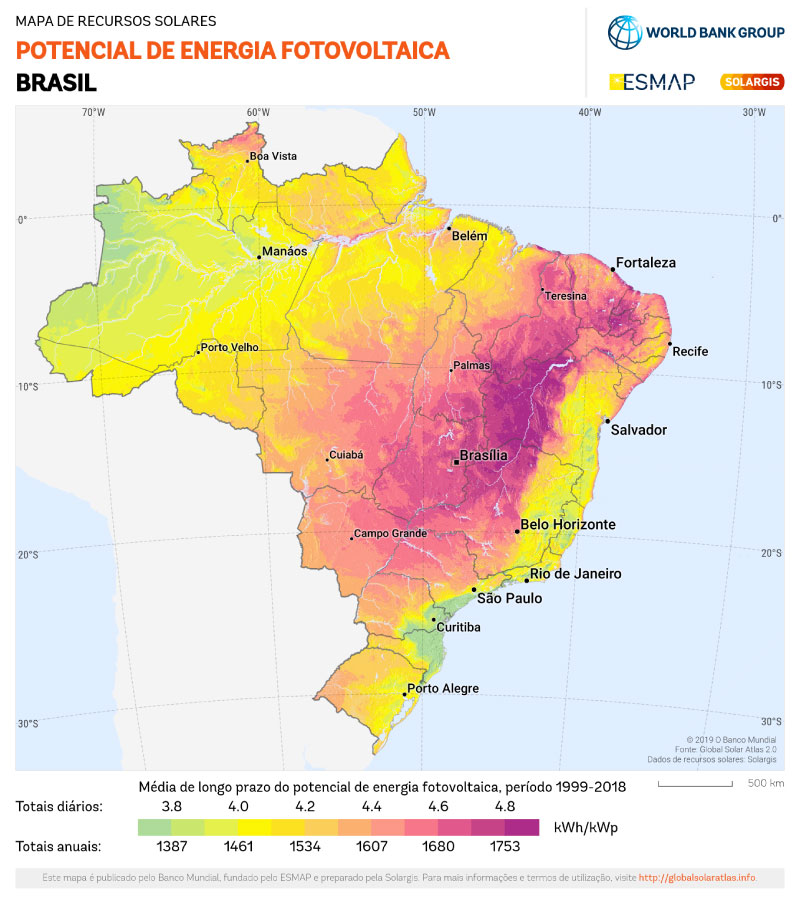
A Figura 2 apresenta o potencial fotovoltaico do Brasil. Observa-se que o interior apresenta o maior potencial e o litoral do sudeste o menor. Adicionalmente, a região próxima ao Equador não possui o maior potencial. 

O Sol

Portanto, o estudo do sol se torna fundamental para entender a energia em nosso planeta. O sol possui as seguintes características:

• • estrela de magnitude 5¹;
  • composto de hidrogênio (77%) e Hélio (21%);
  • massa de 2×10³⁰ kg;
  • raio em 7×10⁵ km;
  • e densidade média em 1 400 kg/m³.

O equilíbrio entre a força explosiva da fusão nuclear e a força de atração da gravidade mantêm a temperatura e a pressão necessárias para estabilizar a estrela emitindo 3,8×10⁸ TW para o espaço. Em decorrência deste equilíbrio, a energia emitida deverá permanecer constante nos próximos bilhões de anos.

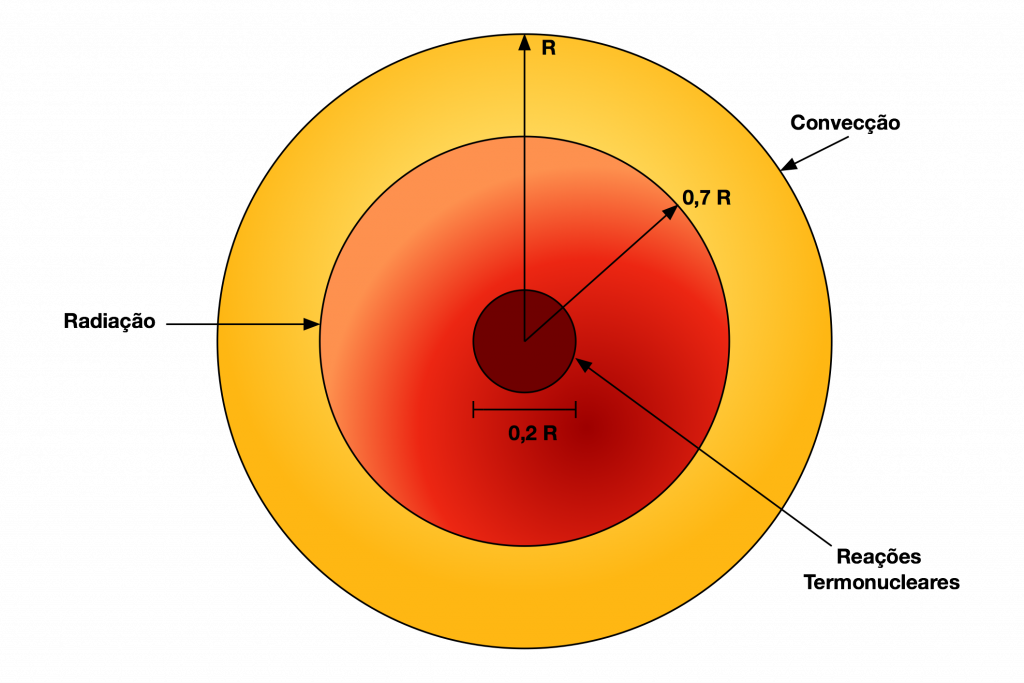
A Figura 3 mostra o modelo do interior do sol.

Reações termonucleares ocorrem no seu centro e a energia flui para o exterior pelos mecanismos de radiação e convecção.

O núcleo apresenta temperatura aproximada de 10⁷ K e densidade 100 vezes maior do que a da água.

A temperatura e densidade diminuem com o aumento da distância ao centro e estabiliza em 5 000 K na superfície.

De acordo com Carroll, as seguintes reações termonucleares produzem a energia do sol. 

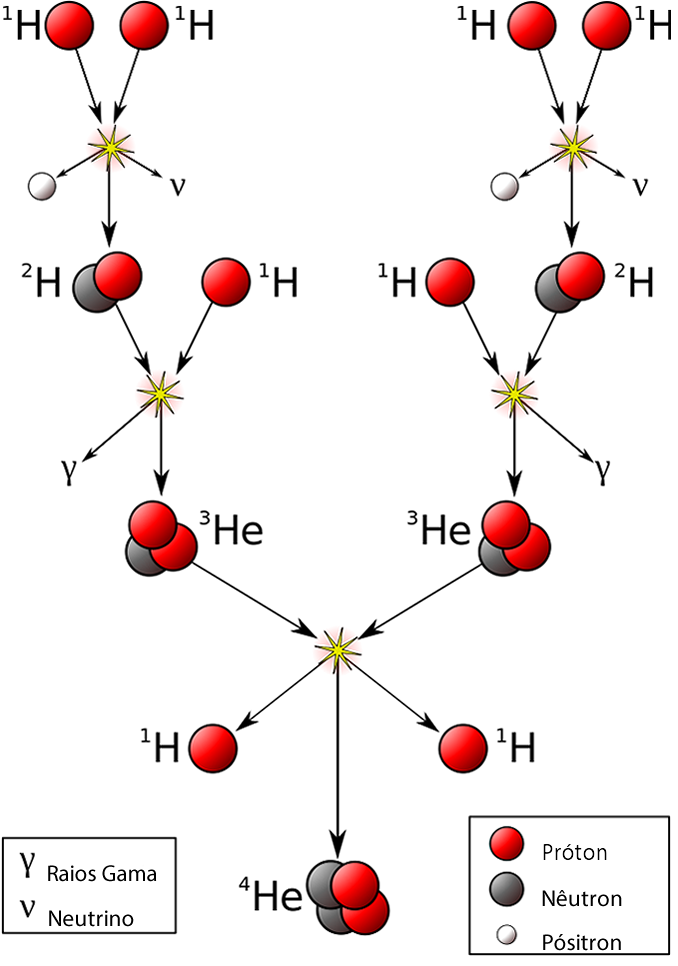
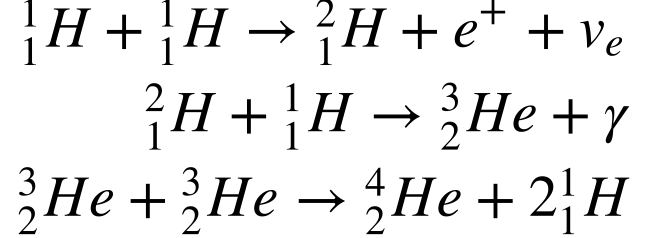
Onde:

• • e⁺ é o pósitron;
  • v_e é o neutrino;
  • γ é a radiação gama.

Estas reações ocorrem com velocidades distintas e liberam diferentes quantidades de energia no núcleo do sol.

A primeira reação da Equação ocorre lentamente (10¹⁰ anos) e libera pouca energia, mas sem ela as demais não poderiam ocorrer.

A segunda reação, muito mais rápida (1 s), libera um pouco mais de energia, e, sem ela, a última também não ocorreria.

Finalmente, a terceira reação, que ocorre numa escala de tempo de 300 000 anos, libera a maior parte da energia – 12,86 MeV. A energia total liberada, para 4 núcleos de Hélio gerados, é de 26,73 MeV. Esta energia equivale ao defeito de massa entre o núcleo de Hélio 4 e 4 prótons livres. Graças às reações mais lentas, o sol emite energia de forma estável durante tanto tempo.

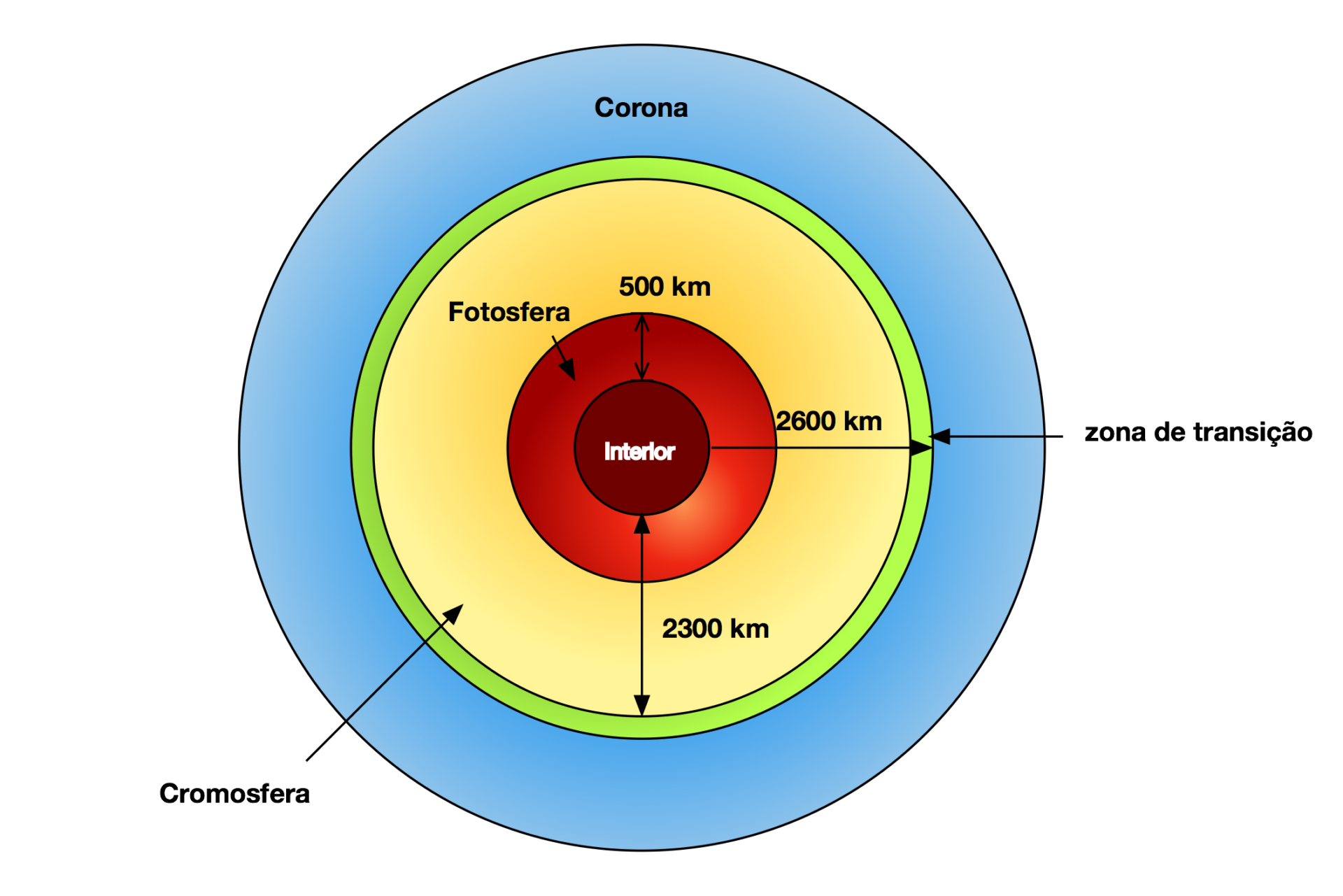
Conforme mostra a Figura 5, os fótons devem atravessar quatro regiões; Fotosfera, Cromosfera, Transição e Corona até iniciarem sua viajem pelo espaço.

Nestas camadas, partículas carregadas formam campos magnéticos intensos que criam fenômenos como explosões solares, manchas solares e o vento solar.

A análise destes fenômenos mostrou possuírem uma periodicidade de aproximadamente 11 anos e afetam o clima na terra.

Energia do Sol

Como inexiste matéria entre a camada mais externa do sol e a terra, a transmissão de energia ocorre pela radiação térmica.

Numa primeira aproximação, pode-se considerar o sol um corpo negro emitindo energia em todo o espectro de frequência e em todas as direções.

A potência emitida por um corpo negro segue a equação de Stefan-Boltzman, e a Astronomia denomina a potência emitida pelas estrelas -E_b– de Luminosidade – L.

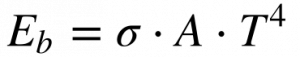
Onde:

• • E_b é a potência emitida por um corpo negro ou Luminosidade da estrela [W];
  • σ é a constante de Stefan-Boltzmann [5,670 373 10^-8 W/(m² K⁴)];
  • A é a área [m²];
  • T é a temperatura [K].

A Irradiância do sol consiste na sua Luminosidade (potência) por unidade de área.

A Irradiância diminui com o inverso da distância ao quadrado, de acordo com a equação abaixo, porque a Luminosidade permanece constante:

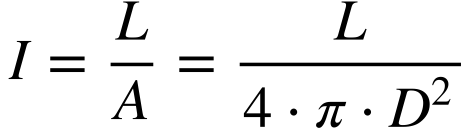
Onde:

• • I é a Irradiância [W m^-2];
  • L é Luminosidade [W];
  • D é a distância entre o sol e o ponto desejado [m].

Denomina-se de Constante Solar a Irradiância do sol na distância de uma unidade astronômica ², que vale aproximadamente 1 361 W m^-2.

Como a distância entre o sol e a terra varia, deve-se ter cuidado ao utilizá-la na solução de problemas práticos.

---

Exemplo 1

Considerando a luminosidade e o raio do sol apresentados na tabela abaixo, determine a temperatura na sua superfície.

Baseado na equação 2, teremos que:

Exemplo 2

Considerando a temperatura calculada no exemplo anterior, estime a irradiância solar na superfície do sol.

A Irradiância será dada por:

Exemplo 3

Determine o comprimento de onda que transmite mais energia do sol.

Baseados na Lei de Wein, o valor máximo da irradiância espectral ocorre sempre para λ.T  for igual a 2 897,8 μm.K. Desta maneira, teremos que:

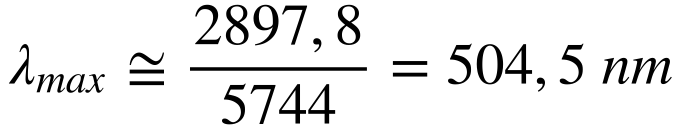Este comprimento de onda se encontra dentro da faixa da luz verde, e parcela significativa da energia solar se encontra na faixa da luz visível.

Em decorrência da seleção natural e evolução das espécies, a visão humana se adaptou a esta faixa de frequências.

---

Tabela 1 – Dados do Sol e da Terra

Fonte: Zombeck

Dados	Valor	Unidade
Constante Solar	1,37	kW/m2
Densidade do núcleo	140 a 180	g/cm3
Densidade Média	1,4	g/cm3
Distância entre o sol e a terra	1,496e8	km
Idade	4,5e9	anos
Luminosidade	3,8e26	W
Massa da Terra	6e24	kg
Massa do Sol	2e30	kg
Período de Rotação	25,05	dias
Radiância Média	2,009e7	W/m2/sr
Raio do sol	7e8	m
Temperatura do Núcleo	15e6	K
Temperatura na Superfície	5800	K

---

Exemplo 4

Qual seria a temperatura de equilíbrio de um planeta sem atmosfera?

Em condições de equilíbrio, a temperatura do permanece constante e o balanço de energia se torna nulo. Isto significa que toda a energia recebida do sol deve ser refletida para o espaço.

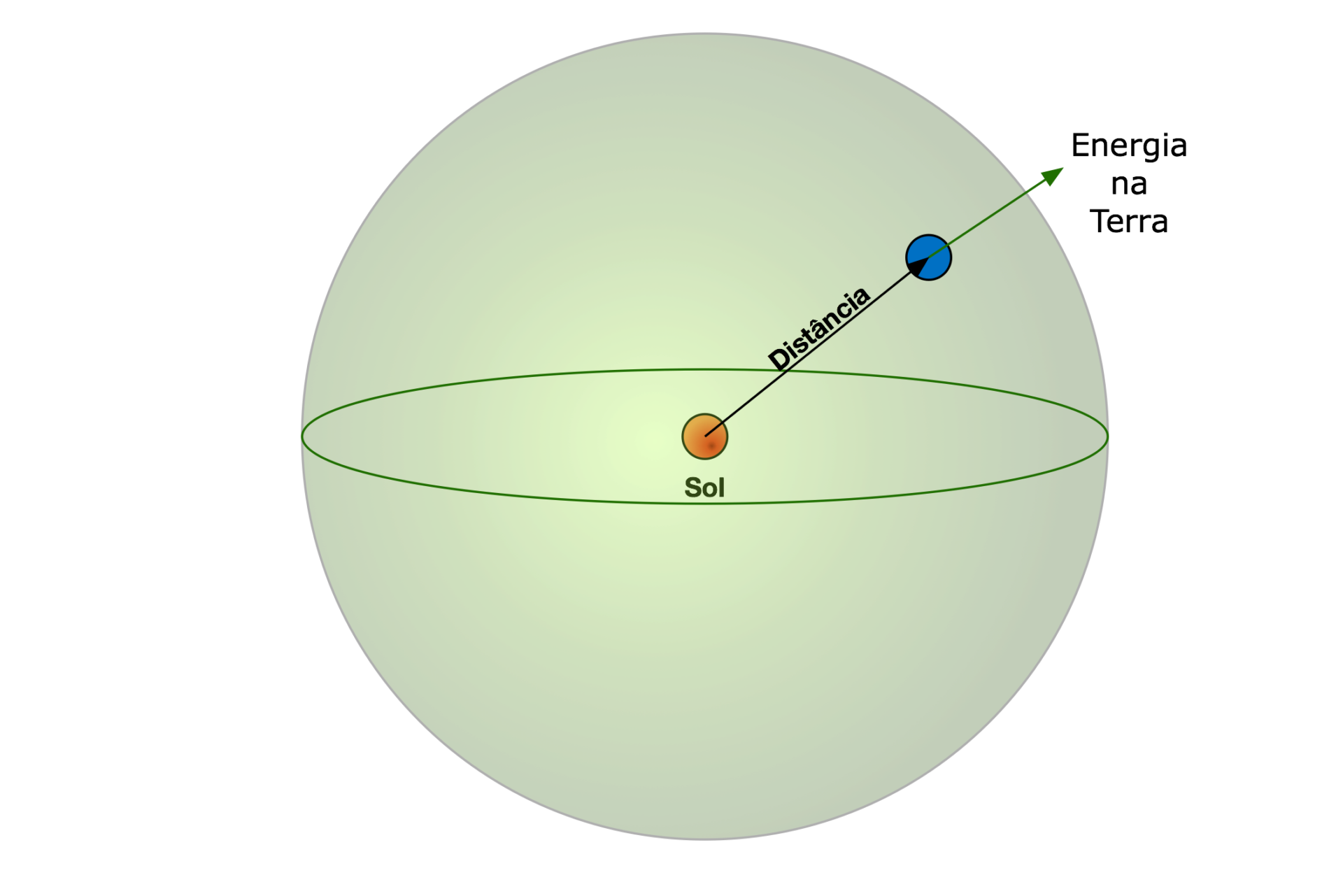
Assumindo que o planeta:

• • • não possui atmosfera;
    • se aproxima de um corpo negro esférico com raio R_t;
    • possui temperatura média uniforme igual a T_t;
    • gira ao redor do sol em órbita circular de raio D_t;
    • reflete para o espaço uma parcela da energia recebida do sol – α,

A equação 2 pode ser aplicada da seguinte maneira:

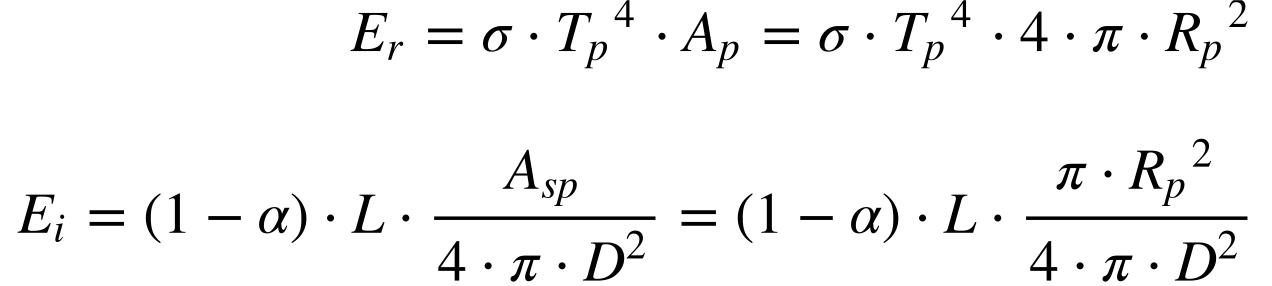
Onde:

• • • E_r é a energia refletida pelo planeta [W];
    • E_i é a energia incidente no planeta [W];
    • T_p é temperatura do planeta [K];
    • A_p é a área de toda a superfície do planeta [m²];
    • A_sp é a área iluminada do planeta [m²];  ³;
    • R_p é o raio do planeta [m];
    • α é o albedo ou coeficiente de reflexão do planeta (energia refletida dividida pela energia recebida)
    • L é a luminosidade solar [W];
    • D é a distância do sol ao planeta [m].

A luminosidade do sol é dada por:

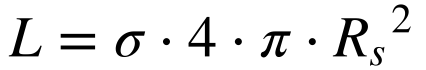
Substituindo a Equação 5 na Equação 4 e igualando a energia recebida à energia refletida, teremos que a temperatura do planeta será dada por:

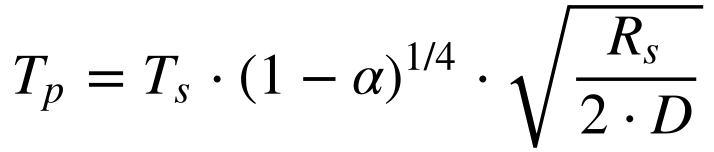
Observa-se que a temperatura do planeta depende do coeficiente de reflexão do planeta, do raio do sol, e da distância entre o planeta e o sol. Curiosamente, ela independe do tamanho do planeta.

Considerando um albedo médio de 30% na terra, sua temperatura de equilíbrio deveria ser de -16 ºC, valor muito abaixo da real temperatura média na superfície.

A influência da atmosfera e do efeito estufa, desconsiderados neste cálculo aproximado, explicam esta discrepância. Portanto, se não existisse o efeito estufa e nem a atmosfera, não teríamos vida como a conhecemos na terra.

Referências

1. 1. ARCHER, D., Global Warming – Understanding the Forecast, 2ª edição, Wiley, 2012.
   2. CARROLL, B.W., OSTLIE, D.A., An Introduction to Modern Astrophysics, 2ª edição, Pearson, 2014.
   3. BADESCU, V., Modeling Solar Radiation at Earth’s Surface, Springer, 2008.
   4. ESCOLA NAVAL, Navegação Astronômica, Ministério da Marinha, 1978.
   5. MILONE, E.F., WILSON, W.J.F., Solar System Astrophysics, Springer, 2008.
   6. SEN, ZEKAI, Solar Energy Fundamentals and Modeling Techniques, Springer, 2008.
   7. WENHAM, S.R., GREEN, M.A., WATT, M.E., CORKISH, R., Applied Photovoltaics, Earthscan, 2007.
   8. ZOMBECK, MARTIN. Handbook of Space Astronomy and Astrophysics., 2nd ed. Cambridge University Press, 2003.
   9. http://rredc.nrel.gov/solar/spectra/am0/ASTM2000.html
   10. https://commons.wikimedia.org/wiki/File:Solar_spectrum_ita.svg
   11. https://en.wikipedia.org/wiki/Earth#/media/File:AxialTiltObliquity.png
   12. Atlas Solar Global
   13. Global Solar Atlas