“Nos próximos cem anos, teremos de cobrir toda a superfície da terra com células solares se quisermos manter o crescimento do consumo energético.”
Jeff Bezos
As células fotovoltaicas ou células solares são os elementos fundamentais da atual tecnologia de energia solar.
Apesar das inúmeras vantagens da energia fotovoltaica, as células solares possuem a menor eficiência de conversão dentre todas as fontes de energia porque absorvem apenas alguns comprimentos de onda da radiação térmica solar.
Células Fotovoltaicas
Junções de semicondutores dos tipos P e N formam a unidade básica das células solares. A Figura 1 mostra o fluxo luminoso dentro dessas unidades.
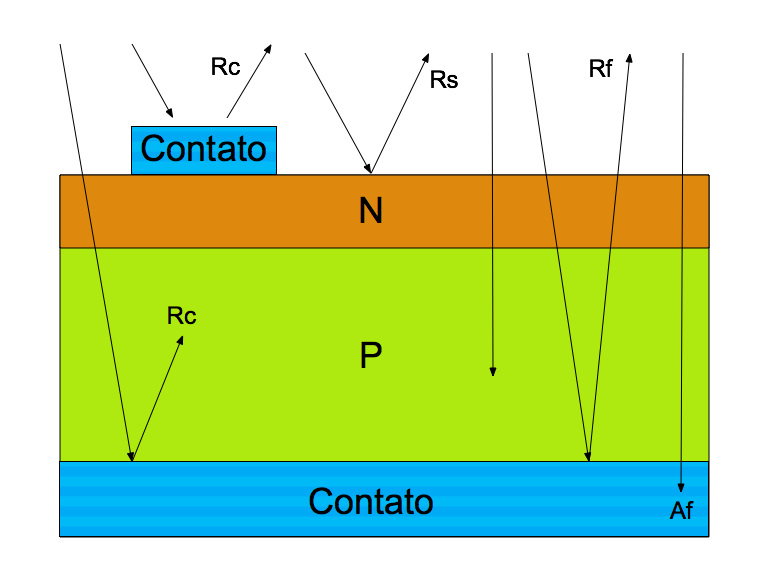
Nem toda a luz solar penetra nas células, porque reflexões ocorrem nos contatos (Rc), na superfície da célula (Rs), e no fundo da célula (Rf). A célula absorve somente parte da energia incidente e parte da refletida pelo fundo da célula. Todas as parcelas refletidas para fora da célula não geram energia e reduzem a sua eficiência. Consequentemente, o projeto das células fotovoltaicas procura minimizar as áreas de contato e a reflexão nas superficies interna e externa.
A absorção de energia ocorre de acordo com a Equação de Planck, que recebeu o prêmio Nobel de Física de 1918.
Planck estabeleceu que a energia se relacionava com a frequência através de uma constante, denominada em sua homenagem de Constante de Planck, conforme mostra a Equação 1.
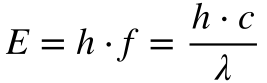
Onde:
-
- E é a energia [J];
- h é a constante de Planck [6,626 069 57 E-34 J.s];
- f é a frequência [Hz];
- c é a velocidade da luz [299 792 458 m/s];
- λ é o comprimento de onda [m].
Einstein demonstrou que o aumento da energia das cargas retiradas pelo efeito fotoelétrico depende do aumento da frequência da luz (sua energia). Além disso, a energia da luz deveria ser maior do que a energia que mantinha a carga presa ao metal. Esta descoberta deu a Einstein o Prêmio Nobel de Física de 1921.
A Mecânica Quântica surgiu, evoluiu e originou os semicondutores. Eles revolucionaram a Eletrônica, criaram os computadores, a Eletrônica de Potência, e a Geração Fotovoltaica.
Portanto, passaram-se 100 anos entre as primeiras descobertas da Física até o crescimento de uma nova tecnologia de Geração de Energia Elétrica.
Pela primeira vez na história, a humanidade se tornou capaz de gerar eletricidade sem partes móveis e de maneira totalmente elétrica.
Materiais Semicondutores
A Figura 2 apresenta os elementos químicos semicondutores responsáveis pela fabricação de todos os dispositivos eletrônicos modernos, e a Tabela 1 apresenta as substâncias químicas formadas por esses elementos para fabricar células solares e dispositivos eletrônicos.
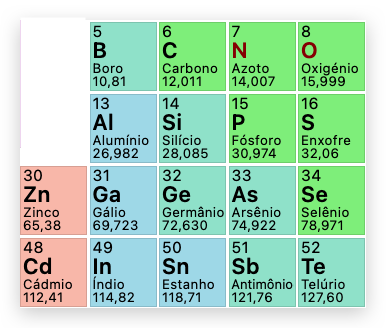
O gap de energia (Eg) dos semicondutores representa a menor energia luminosa necessária para produzir o efeito fotoelétrico. Os valores de Eg variam entre 0,18 eV para o Antimoneto de Indio (InSb) e 3,6 eV para o Sulfeto de Zinco (ZnS) de acordo com a Tabela 1.
| Material | Eg [eV] | μn [cm/(V.s)] | μp [cm/(V.s)] | εr | ⍴m [g/cm3] | Tipo | |
|---|---|---|---|---|---|---|---|
| Material | wdt_ID | Eg [eV] | μn [cm/(V.s)] | μp [cm/(V.s)] | εr | ⍴m [g/cm3] | Tipo |
| Si | 1 | 1,1 | 1.350,0 | 480,0 | 118,0 | 2,3 | Indireto |
| Ge | 2 | 0,7 | 3.900,0 | 1.900,0 | 16,0 | 5,3 | Indireto |
| SiC | 3 | 2,9 | 500,0 | -1,0 | 10,2 | 3,2 | Indireto |
| AlP | 4 | 2,5 | 80,0 | -1,0 | 9,8 | 2,4 | Indireto |
| AlAs | 5 | 2,2 | 1.200,0 | 420,0 | 10,9 | 3,6 | Indireto |
| AlSb | 6 | 1,6 | 200,0 | 300,0 | 11,0 | 4,3 | Indireto |
| GaP | 7 | 2,3 | 300,0 | 150,0 | 11,1 | 4,1 | Indireto |
| GaAs | 8 | 1,4 | 8.500,0 | 400,0 | 13,2 | 5,3 | Direto |
| GaN | 9 | 3,4 | 380,0 | -1,0 | 12,2 | 6,1 | Direto |
| GaSb | 10 | 0,7 | 5.000,0 | 1.000,0 | 15,7 | 5,6 | Direto |
| InP | 11 | 1,4 | 4.000,0 | 100,0 | 12,4 | 4,8 | Direto |
| InAs | 12 | 0,4 | 22.600,0 | 200,0 | 14,6 | 5,7 | Direto |
| InSb | 13 | 0,2 | 100.000,0 | 1.700,0 | 17,7 | 5,8 | Direto |
| ZnS | 14 | 3,6 | 180,0 | 10,0 | 8,9 | 4,1 | Direto |
| ZnSe | 15 | 2,7 | 600,0 | 28,0 | 9,2 | 5,7 | Direto |
| ZnTe | 16 | 2,3 | 530,0 | 100,0 | 10,4 | 5,5 | Direto |
| CdS | 17 | 2,4 | 250,0 | 15,0 | 8,9 | 4,8 | Direto |
| CdSe | 18 | 1,7 | 800,0 | -1,0 | 10,2 | 5,8 | Direto |
| CdTe | 19 | 1,6 | 1.050,0 | 100,0 | 10,2 | 6,2 | Direto |
Tabela 1. Dados dos materiais semicondutores
Exercício Proposto
- Faça um gráfico do gap de energia dos semicondutores da Tabela 1.
- Calcule o comprimento de onda do fóton com a energia do gap de cada um dos elementos.
- Compare os comprimentos de onda encontrados com o espectro de frequências abaixo.
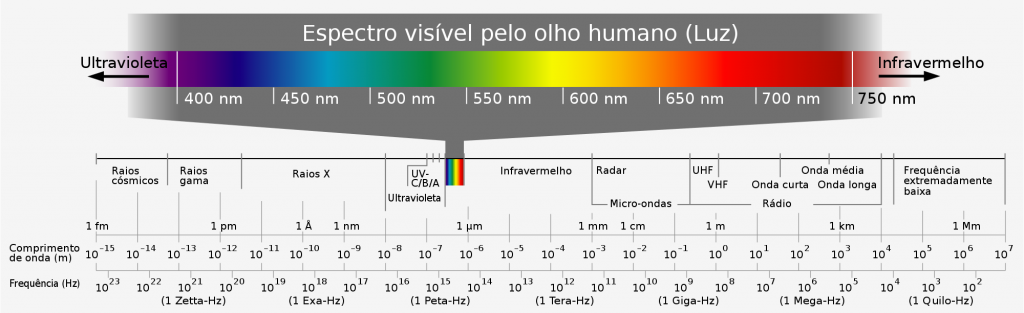
Células Solares
Junções PN de materiais semicondutores formam a estrutura básica das células fotovoltaicas.
Essa escolha resulta da capacidade de criar uma barreira seletiva que resulta numa resistência assimétrica para as cargas P e N. Sem essa barreira, as cargas P e N voltariam a se combinar sem gerar corrente elétrica externa.
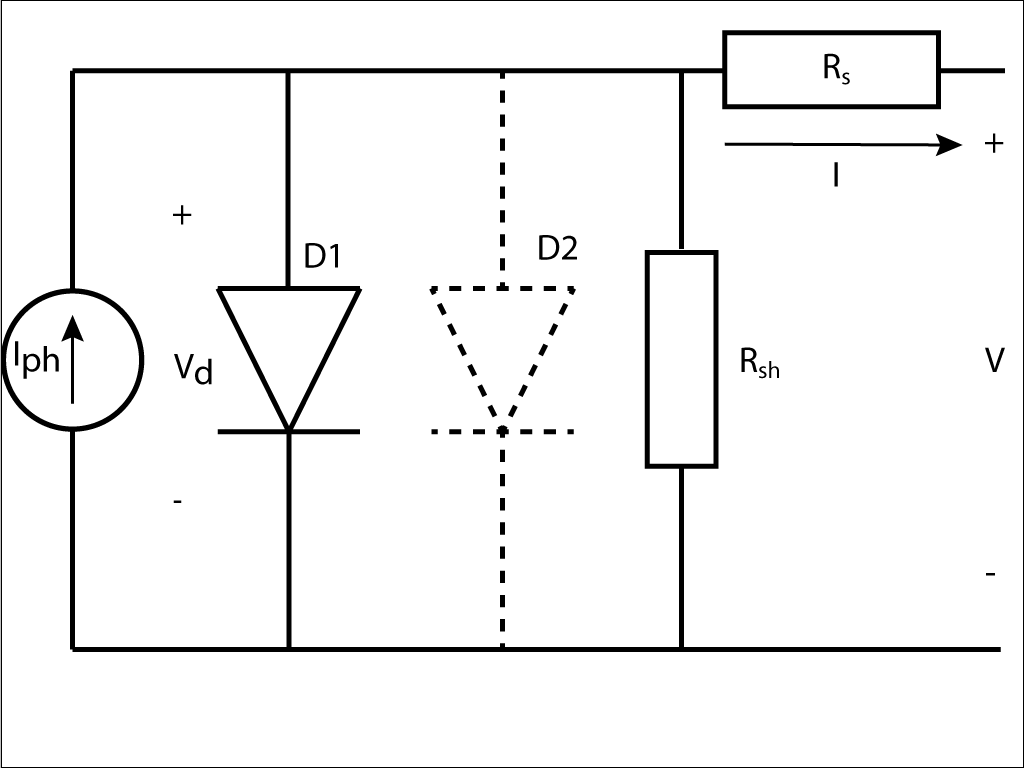
Por serem junções PN, o modelo equivalente de dois diodos da Figura 3 representa as Células Solares.
A fonte de corrente Iph e o diodo D1 representam a célula solar ideal e os demais elementos representam aspectos reais.
A corrente nos semicondutores possui duas componentes; a corrente de difusão e a corrente de recombinação.
Nas células que utilizam materiais semicondutores de gap indireto, pode-se desprezar a componente de recombinação, o caso do Silício. Por outro lado, nos materiais de gap direto ocorre o oposto. 1
A fonte de corrente Iph representa a corrente fotogerada pelos elétrons emitidos pela luz na célula solar.
O diodo D1 representa a junção PN e as resistências representam as perdas. Utiliza-se o diodo D2 para representar alguns fenômenos de segunda ordem.
A tensão V e a corrente I representam as grandezas elétricas disponíveis nos terminais da célula, que dependem da carga e consistem nas únicas grandezas elétricas possíveis de serem medidas na prática.
Corrente Fotogerada
A densidade de corrente fotoelétrica (JL)2 depende da eficiência quântica da célula (Qe), definida como a probabilidade de geração de um elétron a partir da incidência de um fóton de energia E.
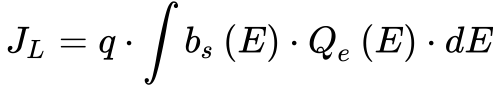
Onde:
-
- JL é a densidade da corrente fotoelétrica;
- q é a carga do elétron;
- bs é a irradiância da luz incidente em função da frequência;
- Qe é a eficiência quântica da célula;
- E é a energia do fóton emitido pela luz, que depende da frequência da luz.
A Eficiência Quântica depende do projeto da célula. Mais especificamente, depende:
-
- do coeficiente de absorção do material utilizado na fabricação do painel fotovoltaico;
- da eficiência da separação das cargas elétricas;
- e da eficiência de coleta das cargas.
Essas características independem do espectro da luz incidente e determinam as diferenças de rendimento entre projetos e materiais utilizados.
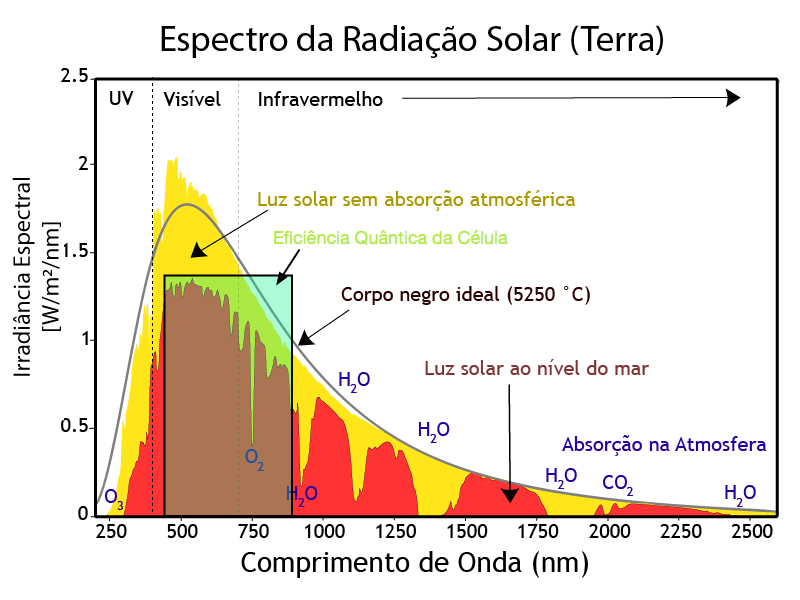
A Figura 4 mostra a irradiância espectral do sol na superfície da terra (curva vermelha) e a eficiência quântica desejada para as células fotovoltaicas (área em verde).
As células devem operar nos comprimentos de onda onde a luz solar apresenta a maior irradiância espectral, mas seu rendimento ficará sempre limitado pela relação entre a área verde da figura e a área vermelha.
Em decorrência disso, deve-se escolher os materiais cujo gap de energia esteja relacionado com comprimentos de onda dentro da área verde.
Exercício Proposto
- Classifique os materiais da Tabela 1 em ordem crescente de eficiência quântica.
Diodo
O diodo constitui o elemento básico da célula fotovoltaica, e, para compreendê-la, torna-se necessário conhecer o funcionamento dos diodos semicondutores.
O diodo representa o único elemento não linear do modelo da célula, e a tensão e corrente se relacionam nele da seguinte maneira:
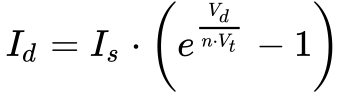
Onde:
-
- Id é a corrente no diodo[A];
- Is é a corrente de saturação reversa do diodo[A];
- Vd é a tensão no diodo[V];
- n é o fator de idealidade do diodo3;
- Vt é a tensão térmica[V].
A corrente de saturação reversa – Is – depende do projeto da célula, mas possui valor muito pequeno.
O fator de idealidade representa as imperfeições e diferenças de fabricação dos diodos reais, variando entre 1 e 2 para os diodos comuns.
Porém, em células fotovoltaicas e dispositivos de potência podem assumir outros valores.
Analisando a Equação 3, observa-se que a corrente do diodo tende para a corrente de saturação reversa quando a tensão no diodo tende para -∞ e tende para infinito quando a tensão tende para +∞.
A Equação 4, obtida a partir da Equação 3, mostra a tensão direta no diodo em função da corrente.
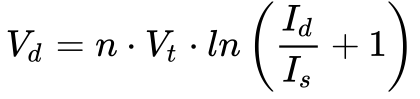
A Equação 5 mostra que a tensão térmica depende da temperatura e surge em decorrência da Mecânica Quântica aplicada aos semicondutores. Isso significa que a temperatura afeta a operação das células fotovoltaicas. 4
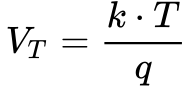
Onde:
-
- Vt é a tensão térmica [V]5;
- k é a constante de Boltzmann [1,380 649 000 00 e-23 J/K]
- q é a carga do elétron [1,602 176 634 00 e-19 C]
- T é a temperatura da junção[K].
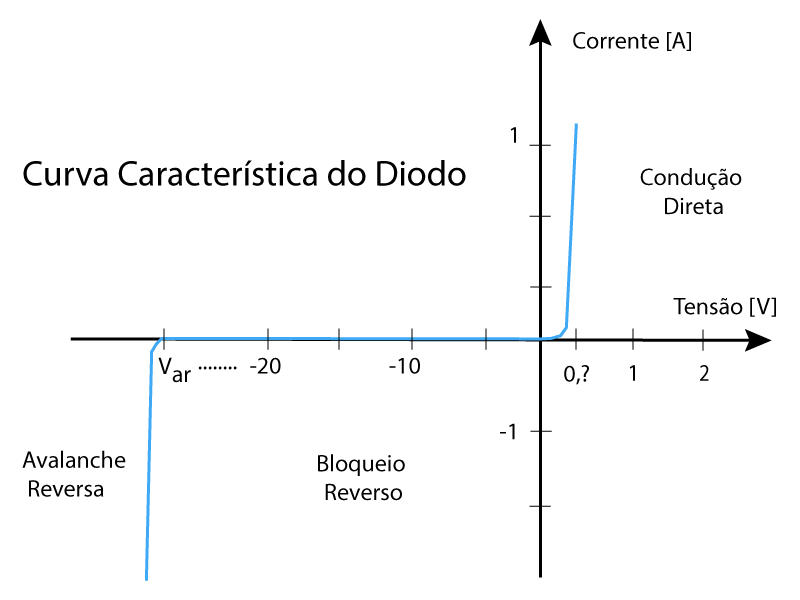
A Figura 5 apresenta a Curva Característica do Diodo para n=1 e t = 300 K.
O eixo da corrente se encontra normalizado em relação à corrente de saturação, e o eixo da tensão se encontra em volts.
Desta maneira, percebe-se que a corrente direta no diodo apresenta valores muito maiores do que a corrente de saturação.
Problemas Propostos
- Calcule o valor da tensão térmica para as temperaturas de 0ºC, 25ºC e 40ºC.
- Faça a curva do diodo para n=2 e compare com a Figura 3
A análise da Equação 3 mostra que, para uma mesma corrente direta, a tensão no diodo aumenta com a temperatura e com o fator de idealidade.
A Figura 4 mostra a tensão direta normalizada no diodo em função da corrente normalizada.
Figura 4. Tensão no Diodo
O circuito da Figura 2 não possui solução analítica devido à não linearidade do diodo. Por isso, torna-se necessário realizar algumas hipóteses simplificadoras.
Inicialmente, com o diodo com tensão direta muito maior que a tensão térmica( Vd>>Vt ) pode-se aproximar a característica do diodo pela Equação 6.
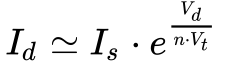
Contudo, a equação permanece não linear.
Por isso, pode-se linearizar a Equação 6 utilizando-se a expansão por uma série de Taylor, conforme a Equação 7.
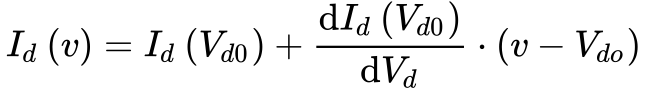
Onde:
-
- v é a tensão linearizada do diodo;
- Vdo é a tensão escolhida para se realizar a linearização;
Inserindo a derivada da Equação 6 na Equação 7, obtém-se a Equação 8.
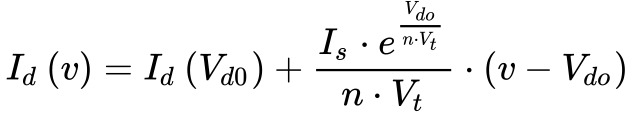
Onde:
-
- Id é a corrente no diodo;
- Vdo é a tensão direta escolhida para realizar a linearização;
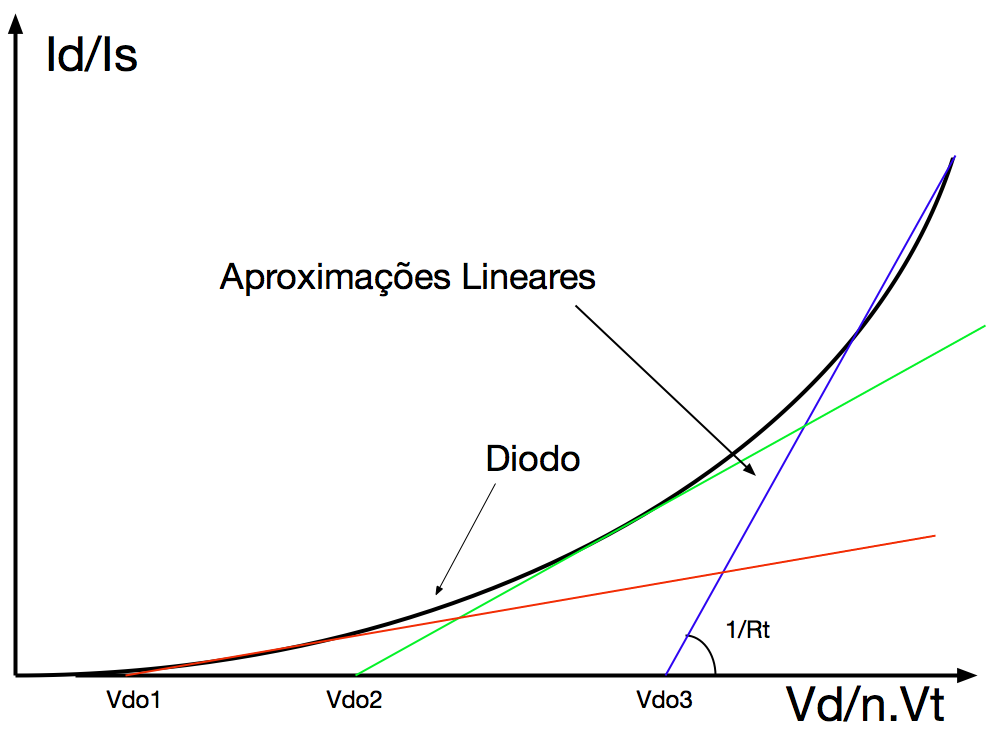
Portanto, o diodo pode ser aproximado por uma fonte de tensão em série com uma resistência dada pela Equação 9.
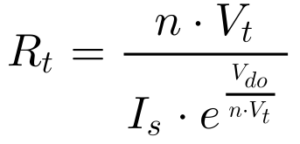
Células Solares Ideais
A Equação 10 fornece a corrente na saída da célula fotovoltaica sem perdas6.
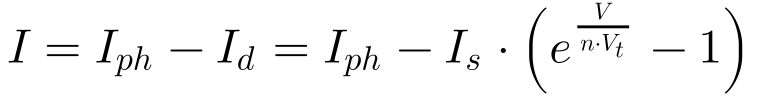
Calcula-se a tensão de saída a partir da Equação 10 da seguinte maneira:
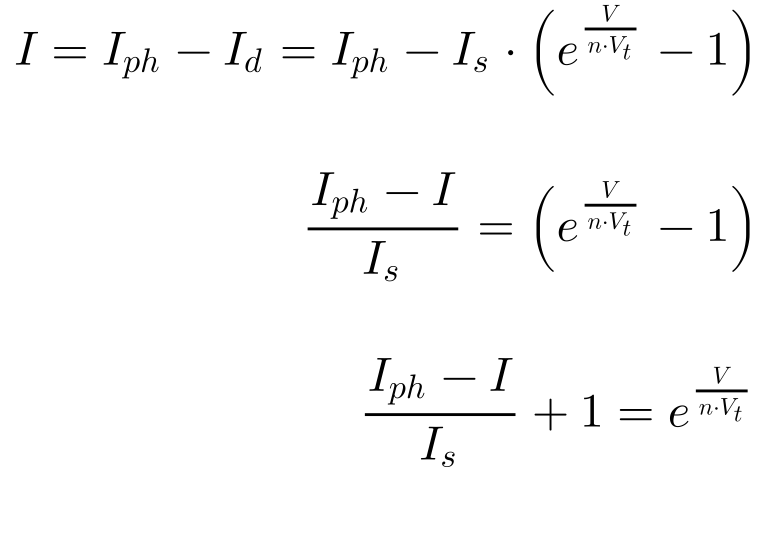
Aplicando logaritmo na equação 11, obtém-se a Equação 12, que fornece a tensão de saída na célula em função da corrente fotogerada e dos parâmetros do diodo.
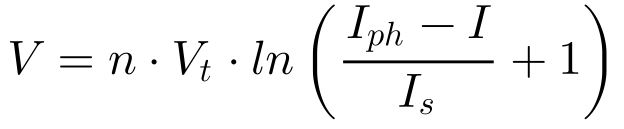
A Equação 13 apresenta a tensão da célula no caso especial de operar sem carga, denominada de tensão em circuito aberto – Voc.
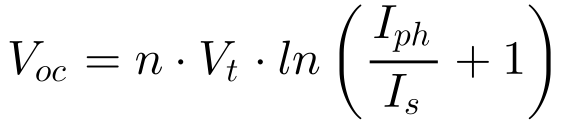
Como Iph>> Is, pode-se aproximar a tensão Voc pela Equação 14.
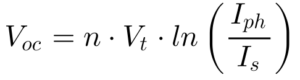
Por outro lado, a Equação 15 fornece a corrente de curto-circuito -Isc– de uma célula ideal a partir da Equação 10.
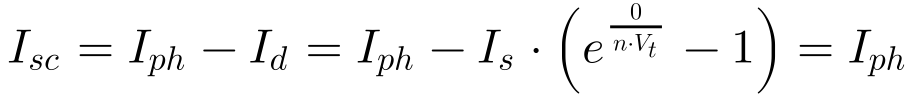
Observa-se que a corrente de curto-circuito na célula ideal depende diretamente da corrente fotovoltaica, mas independe da temperatura.
Por outro lado, aparentemente a tensão de circuito aberto aumenta com a temperatura porque Vt aumenta com a temperatura. Porém, a corrente de saturação reversa -Is- cresce exponencialmente com a temperatura resultando na diminuição de Voc com a temperatura.
Além disso, como a corrente fotovoltaica depende da irradiância solar na célula, ambos os parâmetros aumentam com a irradiância solar.
Pode-se estimar a corrente de saturação reversa – Is -a partir da Equação 11 da seguinte maneira:
Célula Solares com Perdas
O primeiro ajuste no modelo requer a inclusão da corrente na resistência Rsh na equação 10 da seguinte maneira:
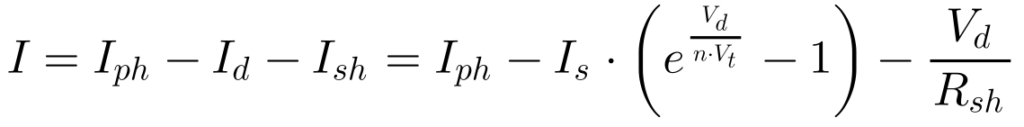
Observa-se que a tensão na equação 16 se tornou a tensão no diodo, não mais a tensão nos terminais da célula, em decorrência da queda de tensão na resistência Rs.
Porém, a tensão no diodo se relaciona com a tensão nos terminais da célula da seguinte maneira:
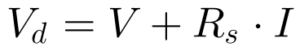
Substituindo-se a Equação 17 na Equação 16, obtém-se corrente de saída da célula em função da tensão em seus terminais conforme Equação 18.
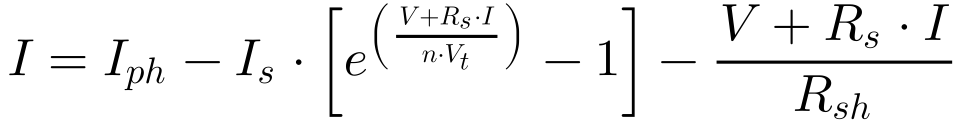
O último aperfeiçoamento considerado na modelagem das células solares consiste na inclusão do segundo diodo que aparece na Figura 3.
Essa inclusão permite simular o fator de idealidade do diodo variando entre 1 e 2 através de um diodo com o valor igual a 1 e outro com o valor de 2.
Curvas Características das Células Solares
A célula solar no escuro se comporta como um diodo porque a corrente fotovoltaica – Iph – é zero. Porém, a corrente nos terminais da célula se iguala à corrente no diodo, mas com sentido negativo, e a célula se comporta como carga dissipando energia fornecida pelo circuito externo.
Essa situação ocorre na prática quando a célula permanece conectada a uma bateria durante a noite sem um diodo de bloqueio.
Quando a célula se encontra iluminada e a corrente fotovoltaica for superior à corrente no diodo, a corrente no circuito externo se torna positiva caracterizando a geração de energia.
A Figura 6 mostra essas duas condições vistas pelo diodo.
A tensão no diodo possui o mesmo sinal da tensão nos terminais, mas as correntes no terminal da célula e fotogerada apresentam o sinal oposto ao da corrente no diodo conforme mostra a Equação 10.
Por isso, a corrente fotogerada desloca a curva do diodo para a região negativa.
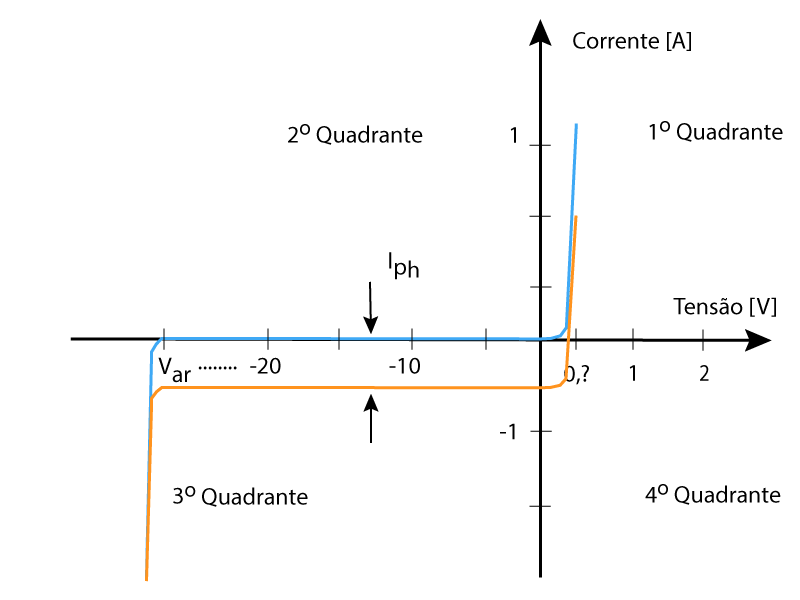
Figura 6. Influência da corrente fotovoltaica no diodo
Como pode-se medir somente a corrente nos terminais da célula, a Figura 7 mostra a curva característica da célula solar tendo como referência a corrente saindo para a carga.
Como o comportamento das células depende da irradiância, temperatura e da localização terrestre, estabeleceu-se uma condição de referência para medir e fornecer os dados dos painéis fotovoltaicos. Essa referência, denominada de STC (standard test conditions) corresponde a uma irradiância de 1 000 W/m2, espectro solar correspondente a AM 1,5, e temperatura na célula de 25ºC.7
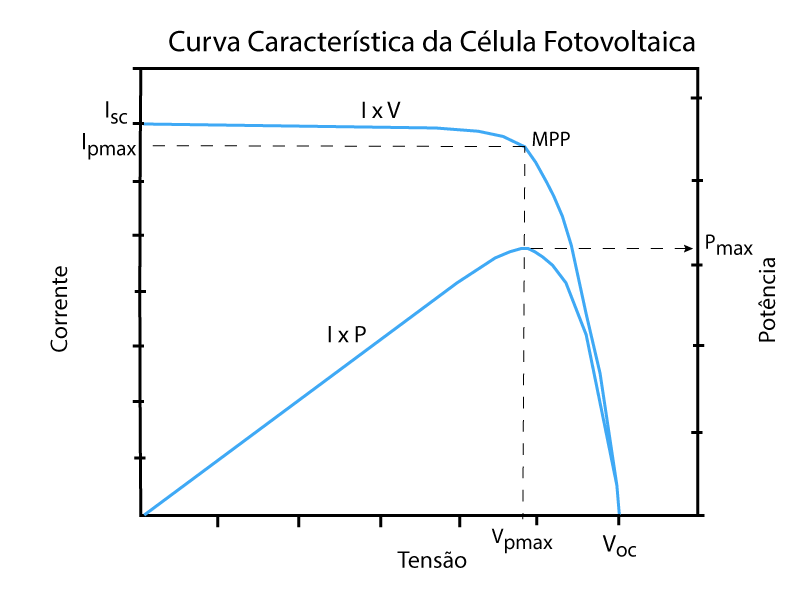
A Figura 7 apresenta características importantes das células solares.
A célula iluminada e em vazio possui uma tensão nos terminais denominada de Voc, e quando em curto-circuito uma corrente Isc.
A tensão Voc aumenta com a irradiância e depende da temperatura, e a corrente Isc também depende da temperatura e irradiância.
De acordo com a Equação 13, Voc possui uma tendência de aumento a temperatura devido à tensão Vt, mas como a corrente Is aumenta exponencialmente com a temperatura, a tensão de circuito aberto decresce com o aumento da temperatura.
Além disso, existe uma potência máxima – Pmax -possível de ser gerada pelas células solares para cada condição de irradiância, temperatura e localização geográfica.
Como irradiância e temperatura variam ao longo do dia, o ponto de máxima potência varia ao longo do tempo. Isto significa que uma célula alimentando uma carga resistiva constante fornece potência máxima apenas em uma condição particular.
Exemplo
A Tabela abaixo apresenta os dados fornecidos pelo fabricante para o painel BP-MSX 120 e a Figura 8 sua curva características medida por um traçador de curvas após anos de exposição ao tempo e a curva de catálogo para um painel novo.
Dados obtidos de BP solar 2001 01-4003-1Painel BP-MSX 120
wdt_ID Parâmetro Simbolo Unidade Valor Precisão Observações
1
Potência Máxima
Pmax
W
120,000
STC
2
Tensão em Pmax
Vmp
V
33,700
STC
3
Corrente em Pmax
Imp
A
3,560
STC
4
Corrente de curto- circuito
Isc
A
3,870
STC
5
Tensão em aberto
Voc
V
42,100
STC
6
Coeficiente de variação de Isc com a temperatura
Ki
%/ºC
0,065
0,015
STC
7
Coeficiente de variação de Voc com a temperatura
Kv
mV/ºC
-160,000
10,000
STC
8
Tensão máxima
Vmax
V
600,000
STC
9
Número de células em série
Ns
72,000
STC
10
Número de células em paralelo
Np
0,000
STC
11
Coeficiente de variação de Pmax com a temperatura
Kp
%/ºC
-0,500
0,050
STC
12
Temperatura nominal de operação da célula
NOCT
ºC
47,000
2,000
STC, Tamb=20ºC ,800W/m2, 1m/s vento
13
Espessura de vidro em cada face
mm
3,000
STC
14
Proteção de cada face - Ethylene vinyl acetate
STC
15
Altura
A
mm
1.114,000
3,000
STC
16
Largura
L
mm
991,000
3,000
STC
17
Peso
P
kg
13,000
STC
18
Pmax mínimo garantido
Pmin
W
114,000
STC
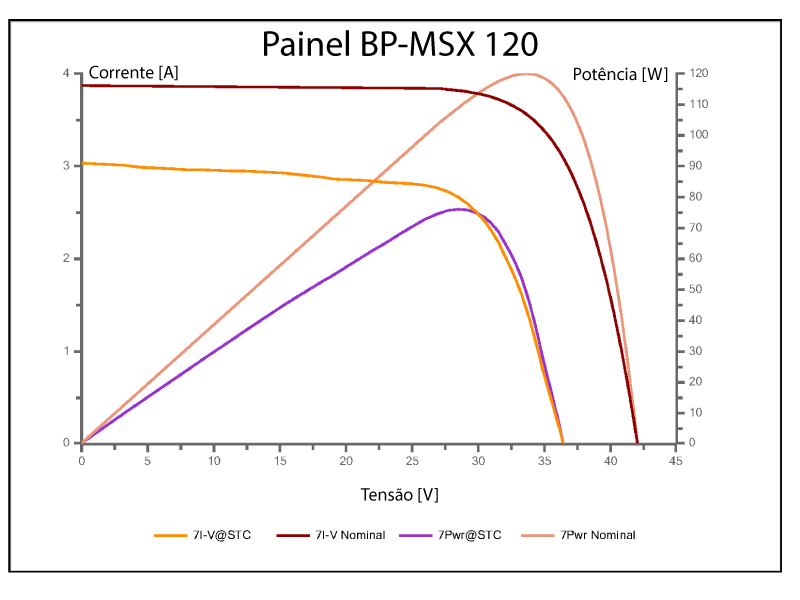
Observam-se as seguintes modificações entre as curvas degradadas e as novas:
- A potência máxima gerada diminuiu;
- As inclinações da curva IxV mudaram.
Referências
- HÄBERLIN, H.; Photovoltaics: System Design and Practice, Wiley, 2012.
- KITAI, A.; Principles of Solar Cells, LEDs and Diodes, Wiley, 2011.
- HEGEDUS, Steven; LUQUE, Antonio (Ed.). Handbook of photovoltaic science and engineering. John Wiley & Sons, 2011.
- McEVOY, A, Castaner, L., Markvart, T.; Solar Cells: Materials, Manufacture and Operation, 2 Ed., Academic Press, 2012.
- NELSON, J; The Physics of Solar Cells, Imperial College, 2003.
- SMESTAD, G. P.; Optoelectronics of Solar Cells, SPIE.Digital Library, 2002.
- WENHAM, S.R., GREEN, M.A., WATT, M.E., CORKISH, R., Applied Photovoltaics, Earthscan, 2007.
- WÜRFEL, P., Physics of Solar Cells: From Principles to New Concepts, Wiley, 2005.
