As turbinas eólicas surgiram na antiguidade e a Figura 1 mostra a primeira aplicação prática registrada. Esta instalação em Sistan na Pérsia data o século VII, servia para moer grãos e seu eixo de rotação se encontrava na vertical.

Na Europa, os primeiros cataventos surgiram somente no século XI trazidos pelos cruzados, e os famosos moinhos Holandeses apareceram no século XIV.

O avanço tecnológico dos moinhos holandeses permitiu que a oferta de comida aumentasse na Europa, frustrou as previsões de Malthus e contribuiu para a Holanda se tornar uma potência econômica através da Companhia Holandesa das Índias Orientais e Ocidentais.
Tipos de Turbinas Eólicas
Existem dois tipos básicos de turbinas eólicas:
-
- Horizontais;
- Verticais.
As turbinas horizontais possuem o eixo de rotação horizontal (Figura 3), e as turbinas verticais operam com o eixo de rotação na vertical (Figura 4).


A principal vantagem das turbinas verticais consiste na independência da direção do vento. Apesar disso, as turbinas horizontais dominam o mercado atual de turbinas eólicas para geração de energia.
As turbinas eólicas funcionam de forma semelhante às as turbinas hidráulicas e as hélices de aviões e helicópteros.
Análise das Turbinas Horizontais
A análise das turbinas eólicas envolve conceitos avançados de aerodinâmica e mecânica dos fluidos, mas obtém-se conclusões importantes a partir de simplificações.
A energia contida no vento horizontal consiste basicamente na sua energia cinética, uma vez que não há variação de pressão nem variação de altitude, conforme a seguinte expressão:
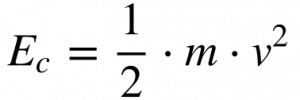
Onde:
-
- Ec é a energia cinética;
- m é a massa;
- v é a velocidade.
Todavia, a aplicação desta expressão na análise das turbinas eólicas apresenta algumas dificuldades.
De acordo com Burton, a Figura 5 mostra uma primeira aproximação para o fluxo de ar através de um rotor de uma turbina eólica, onde:
-
- Vinf é a velocidade do vento muito antes de sofrer influência do rotor;
- Pinf é a pressão do ar sem sofrer influência do rotor;
- Ve é a velocidade do vento na esteira do rotor;
- Vd é a velocidade do vento no rotor;
- Pd é a pressão do ar no rotor;
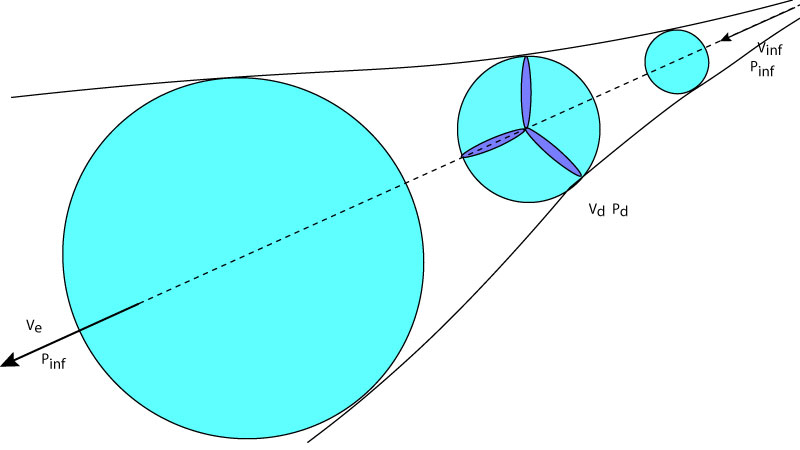
Figura 5. Modelo da turbina eólica
A energia retirada pela turbina reduz a energia do vento após a turbina em decorrência da lei de conservação de energia. Isto acarreta redução da velocidade do vento após o rotor (Ve), e quanto maior a energia gerada, menor será essa velocidade.
Além da conservação de energia, a turbina deve obedecer também à conservação de massa. Numa primeira aproximação, podemos considerar apenas a massa de ar que atravessa o rotor, isto é, apenas a massa de ar contida no tubo fictício, apresentado na Figura 1.
Isto significa que não existe fluxo de ar para dentro ou para fora deste duto imaginário e, consequentemente, a conservação de massa se aplica a todo o duto conforme a expressão abaixo:
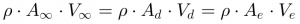
Onde:
-
- ρ é a densidade do ar;
- A é a área;
- V é a velocidade.
A expressão abaixo relaciona a velocidade do vento no disco da turbina com a velocidade do vento a montante através de um fator, denominado de fator de indução de fluxo axial (a). Esse fator varia entre 0 e 1, sendo nulo quando a turbina se encontra parada e 1 se a turbina fosse sólida.
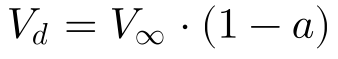
Substituindo esta expressão na Equação 2, obtêm-se que:
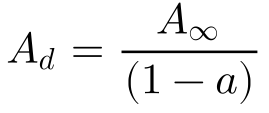
Observa-se que a redução da velocidade do vento, causada pelo rotor da turbina, aumenta a área do tubo fictício a jusante do rotor proporcionalmente à redução da velocidade devido à conservação de massa.
Além disso, essa redução de velocidade produz uma variação no momento linear da massa de ar.
Como variação de momento linear significa força, pode-se igualar a variação do momento linear do ar com a força exercida no disco da turbina.
Por sua vez, a força no disco equivale à área do disco vezes a pressão exercida pelo vento, conforme a Equação 5.
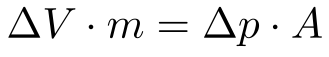
Onde:
-
- ΔV é a variação de velocidade do ar;
- m é a massa do ar;
- Δp é a variação de pressão no disco da turbina;
- A é a área do disco da turbina.
As equações abaixo fornecem a variação total de velocidade do vento, a massa de ar e a variação de pressão no disco da turbina.
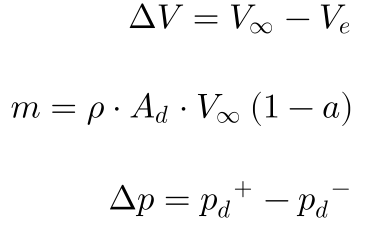
Substituindo essas expressões na Eq.5, resulta que:
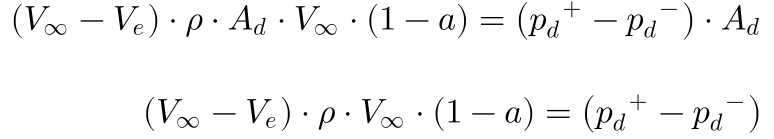
A equação de Bernoulli estabelece que a energia permanece constante em fluidos incompressíveis quando não existe realização de trabalho nem transferência de calor.
Matematicamente, pode se escrever da seguinte maneira:
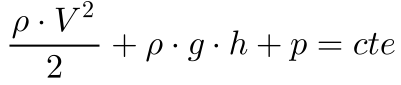
Onde:
-
- v é a velocidade;
- ρ é a densidade do fluido;
- g é a aceleração da gravidade;
- h é a altura com relação a uma referência;
- p é a pressão.
Aplicando a equação de Bernoulli às duas seções do tubo fictício e, considerando o sistema horizontal, a altura h desaparece da equação. Apesar do ar não ser incompressível, utiliza-se esta hipótese simplificadora.
Desta maneira, têm-se que:
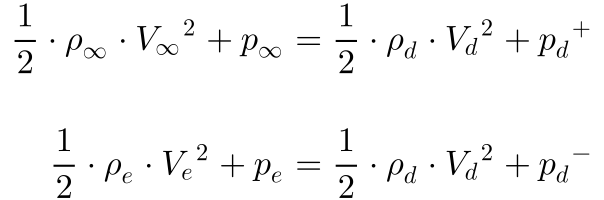
Considerando que a atmosfera equaliza as pressões antes e depois da turbina e subtraindo uma equação da outra, pode-se escrever que:
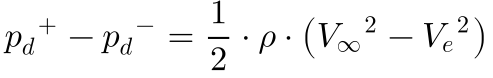
A Equação 10 mostra que a variação da velocidade do vento ocorre metade antes e metade depois do disco da turbina.
A substituição da Equação 10 na Equação 7 permite calcular a velocidade do vento na esteira da turbina:
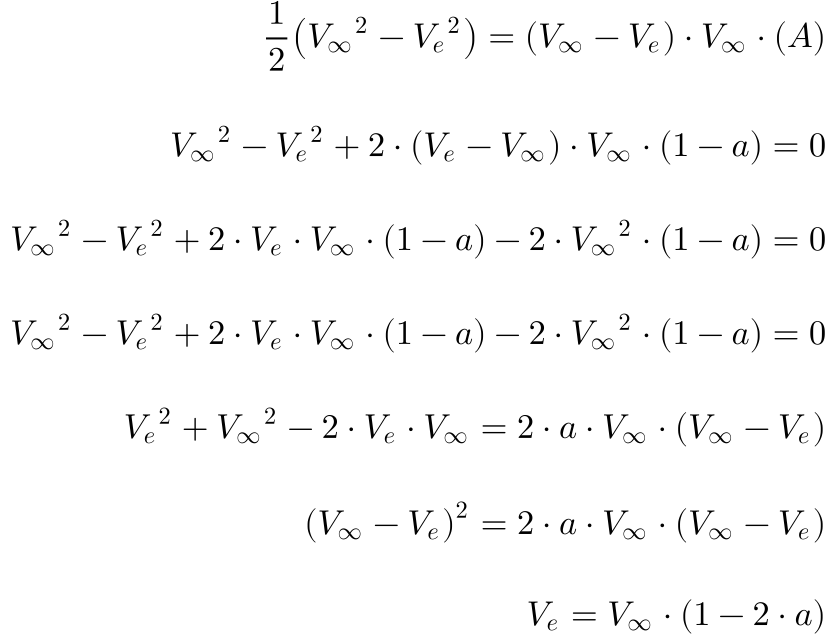
Por sua vez, a Equação 12 fornece a força exercida pelo vento no disco fictício da turbina.
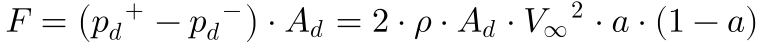
Define-se potência como a derivada no tempo do trabalho, que por sua vez resulta do produto escalar da força pela posição.
Logo, o produto da força pela velocidade do vento no disco da turbina determina a potência extraída pela máquina conforme a Equação 13.
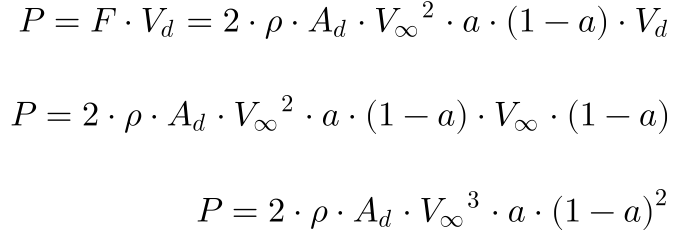
Portanto, de acordo com a Equação 13, a potência extraída pela turbina depende da área da turbina e do cubo da velocidade do vento.
Por outro lado, a potência existente no vento sem a turbina será dada por:
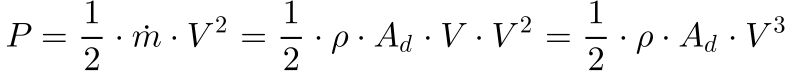
A Equação 15 apresenta a potência extraída pela turbina como uma parcela da energia contida no vento.
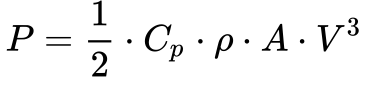
Onde:
-
- P é a potência mecânica extraída pela turbina;
- Cp é o coeficiente de potência;
- ρ é a densidade do ar;
- A é a área da turbina;
- V é a velocidade do vento.
Por sua vez, define-se o Coeficiente de Potência – Cp – como a potência na turbina, definida na Equação 14, dividida pela potência existente no vento da seguinte maneira:
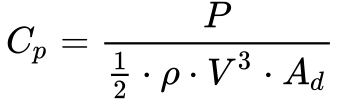
Deve-se observar que, como a densidade do ar vale 800 vezes menos do que a densidade da água, a potência fornecida por turbinas eólicas é muito menor do que a potência gerada pelas turbinas hidráulicas.
Além disso, conforme mostra a Figura 6, a densidade do ar varia com a temperatura e com a altitude.
Figura 6. Densidade do ar
O coeficiente de potência representa a fração máxima da energia contida no vento que pode ser extraída pela turbina e, combinando as Equações 13 e 16, obtém-se a seguinte expressão:
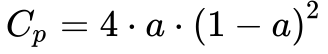
Portanto, a potência máxima possível de ser extraída do vento foi calculada por Albert Betz1 derivando a Equação 17 e igualando a zero.
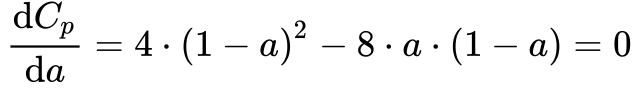
Resolvendo a Equação 18, obtém-se que a=1/3 maximiza Cp. Substituindo este valor na Equação 17, obtém-se que:
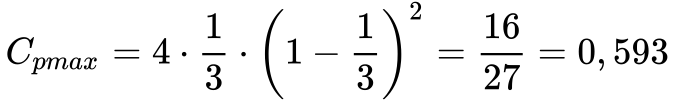
Este valor de aproximadamente 60% tornou-se conhecido como o limite de Betz e representa o valor máximo de potência possível de ser extraído do vento por qualquer turbina horizontal.
Pode-se também normalizar a força exercida no rotor – Equação 12 – utilizando a energia do vento como base.
Desta maneira, define-se o coeficiente de torque -Ct – de acordo com a seguinte expressão:
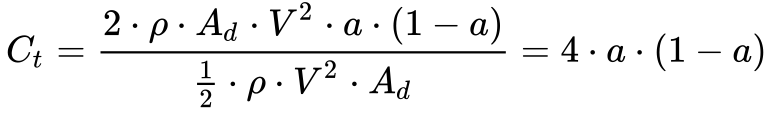
A Figura 7 apresenta os coeficientes de Potência e Torque em função do fator de indução de fluxo axial – a, e a Figura 8 os mesmos coeficientes em função da relação Vd/V∞.
A partir da Equação 3, obtém-se que este parâmetro representa a relação entre a velocidade do vento a montante e a velocidade do vento na turbina de acordo com a Equação 21.
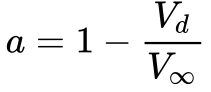
A Equação 21 mostra que o fator de indução de fluxo axial varia entre 0 e 1, enquanto o valor de Vd varia de V∞ e 0 respectivamente.
Isto significa que a potência e o torque se anulam nestes dois pontos extremos.
Além disso, o limite de Betz, que ocorre para o fator igual a 1/3, implica que a velocidade na turbina deve ser 70% da velocidade do vento a montante.
Por outro lado, o coeficiente de torque máximo ocorre para a=1/2, que corresponde a uma velocidade de vento na turbina de 50%.
O projeto específico da turbina determina como a energia cinética do vento se transforma em energia mecânica.
No entanto, a maioria das turbinas atuais utiliza rotores com determinado número de pás que giram com velocidade angular – ω – paralela à direção do vento e ortogonal ao plano das pás.
As pás giram ao longo da área Ad e, devido ao seu projeto aerodinâmico, criam a diferença de pressão ao longo da área que reduz o momento no fluxo do vento e converte a energia do vento em energia mecânica.
O eixo do rotor da turbina se encontra acoplado a um gerador de energia elétrica que completa a conversão da energia mecânica em energia elétrica.
Neste processo, o gerador gera um torque, em sentido contrário ao torque exercido pelo vento e proporcional à energia elétrica gerada. Em condições de equilíbrio, estes torques se igualam e a velocidade angular permanece constante.
A geração do torque no rotor pela passagem do vento produz um torque igual e contrário no ar. Isto significa que o ar, após o rotor da turbina, adquiri um momento angular com rotação contrária à rotação do rotor, que inexistia no vento a montante da turbina.
Esta variação de momento e velocidade angular representa um aumento na energia cinética, que é compensado pela queda de pressão no ar a jusante do rotor.
Referências
- Burton, T., Sharp, D., Jenkins, N., Bossanyi, E., Wind Energy Handbook, Wiley, 2001.
- Betz, A., Introduction to the Theory of Flow Machines, Pergamon Press, 1966.2
- INTERNATIONAL ELECTROTECHNICAL COMMISSION, IEC 61400-1 Wind Turbines – Part 1: Design Requirements, 3 Ed., IEC, 2005
