Geração de Energia a Vapor

“A Primeira Revolução Industrial usou água e vapor para mecanizar a produção. A Segunda utilizou energia elétrica para criar a produção em massa. A Terceira empregou a eletrônica e tecnologia da informação para automatizar a produção.”

Klaus Schwab

A aplicação do vapor como força motriz se tornou realidade a partir dos trabalhos de Thomas Savery em 1698, e deu origem à geração de energia a vapor. Estes trabalhos resultaram no motor alternativo a vapor que originou a revolução industrial, as ferrovias, os navios a vapor e a geração de energia elétrica.

As primeiras usinas termelétricas surgiram em 1882 em Nova Iorque¹ e em Londres² utilizando motores alternativos a vapor. Em 1901 entrou em operação a maior usina construída com esses motores para a Manhattan Elevated Railway. Essa usina possuía 17 motores de 500 toneladas cada um e capacidade total de 6 MW.

O desenvolvimento da turbina a vapor demorou, mas, uma vez iniciado, foi rápido. Entre o final do século XVIII e o século XIX, diversos pesquisadores trabalharam em paralelo e mais de 100 patentes surgiram entre 1880 e 1883. As primeiras turbinas a vapor foram construídas por Carl Gustav de Laval, do tipo impulso, e Charles Parsons, do tipo reação, e esta tecnologia dominou a geração termelétrica a partir de 1905.

Por exemplo, uma usina de mesma potência com turbinas a vapor pesaria apenas 20% do peso da usina Manhattan Elevated Railway.

Portanto, a relação Peso/Potência tornou-se um índice importante de avaliação de máquinas. Máquinas de igual potência, mas mais pesadas, desaparecem do mercado se a eficiência for igual.

A Figura 1 mostra uma termelétrica a carvão construída na Alemanha no final do século XX. Observa-se que diversos controles ambientais, tais como esteiras transportadoras cobertas, foram utilizados.

---

Schwarze Pumpe
Location:  Bradenburg & Mecklenburg – Alemanha
Operador: Vattenfall Europe AG
Configuração: 2 X 800 MW
Início de Operação: 1997-1998
Combustível: Linhito
Fabricante da Caldeira: EVT
Fabricante das Turbinas e Geradores: Siemens

---

A segunda lei da termodinâmica estabelece o conceito de rendimento térmico.

É teoricamente impossível construir uma máquina térmica que transforme todo o calor recebido de uma fonte quente em trabalho ou que transfira calor de uma fonte mais fria para uma fonte mais quente sem consumir trabalho.

Então, a grande questão passa a ser:

• • Qual a maior eficiência teórica possível de ser obtida?

O físico e engenheiro militar francês Nicolas Leonard Sadi Carnot (1796-1832) resolveu esta questão em 1824. De acordo com Carnot, nenhuma máquina térmica poderia apresentar um rendimento superior a:

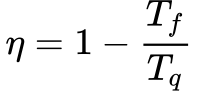
Onde:

• • η é o rendimento [%];
  • T_f é a temperatura da fonte fria[K];
  • T_q é a temperatura da fonte quente[K];

Porém, o rendimento real depende do ciclo termodinâmico que mais se assemelha ao da máquina térmica, mas todos se mostraram inferiores ao rendimento de Carnot.

---

Problema Proposto

Utilizando a fórmula do rendimento de Carnot, calcule a eficiência de uma máquina térmica cuja fonte quente se encontre a 212 °C e a fonte fria a 45 °C.

---

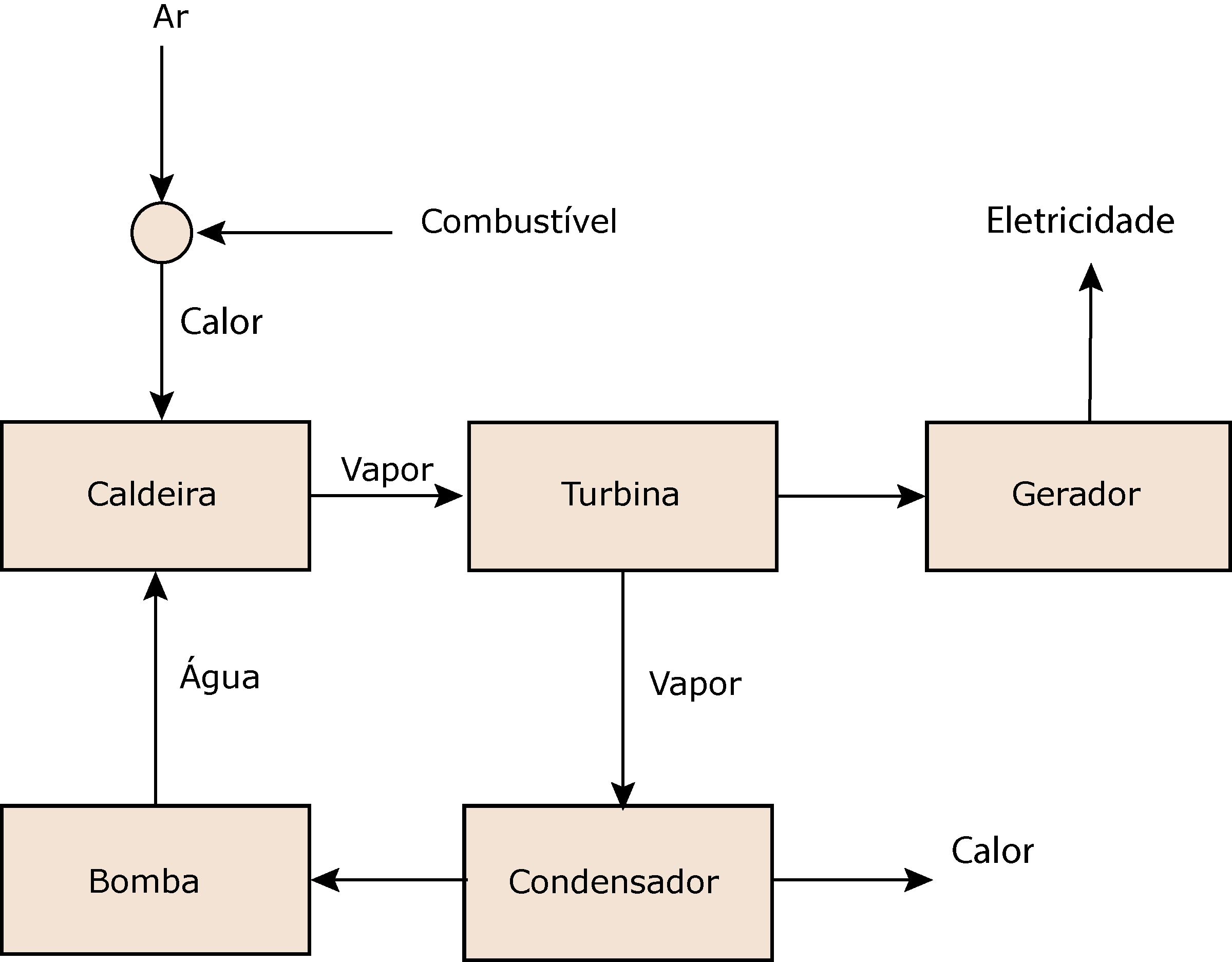
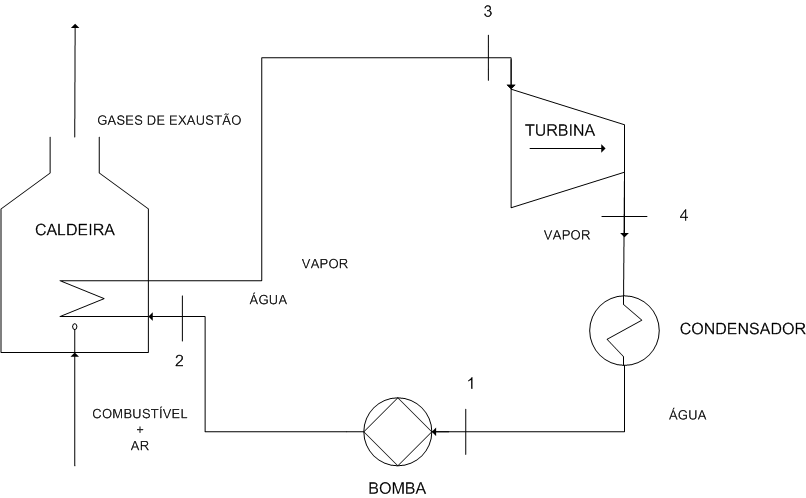
Atualmente, a geração de energia elétrica, utilizando o vapor, se baseia na turbina a vapor³, conforme mostra a Figura 2. 

A combustão da mistura combustível-ar produz calor na caldeira que transforma a água em vapor.

Em seguida, injeta-se o vapor na turbina para gerar trabalho mecânico que aciona o gerador.

Por sua vez, o vapor na saída na turbina se transforma novamente em água ao passar pelo condensador. Nesta operação, devolve-se o calor retirado para o meio ambiente.

Finalmente, a água sai do condensador para a bomba que injeta novamente a água com a pressão adequada na caldeira. Desta maneira, o ciclo termodinâmico se completa.

Água

A água se tornou o fluido de trabalho preferido devido às suas excelentes propriedades térmicas⁴ e disponibilidade na terra.

Define-se o estado termodinâmico das substâncias por quaisquer duas das sete propriedades termodinâmicas:

• • Temperatura[K];
  • Pressão [Pa];
  • Volume Específico[m³/kg];
  • Energia interna[J];
  • Entalpia[J] ou Entalpia Específica[J/kg];
  • Entropia[J/K] ou Entropia Específica[J/(kg.K)];⁵
  • Título.

O vapor de água tem sido extremamente estudado e suas propriedades se encontram documentadas pela International Association for Properties of Water and Steam – IAPWS. Este documento apresenta os fundamentos atualmente válidos para determinar as propriedades termodinâmicas do vapor d’água para utilização industrial.

Utilizaremos no curso o programa Fluid Properties Calculator  para realizarmos os cálculos necessários. ⁶

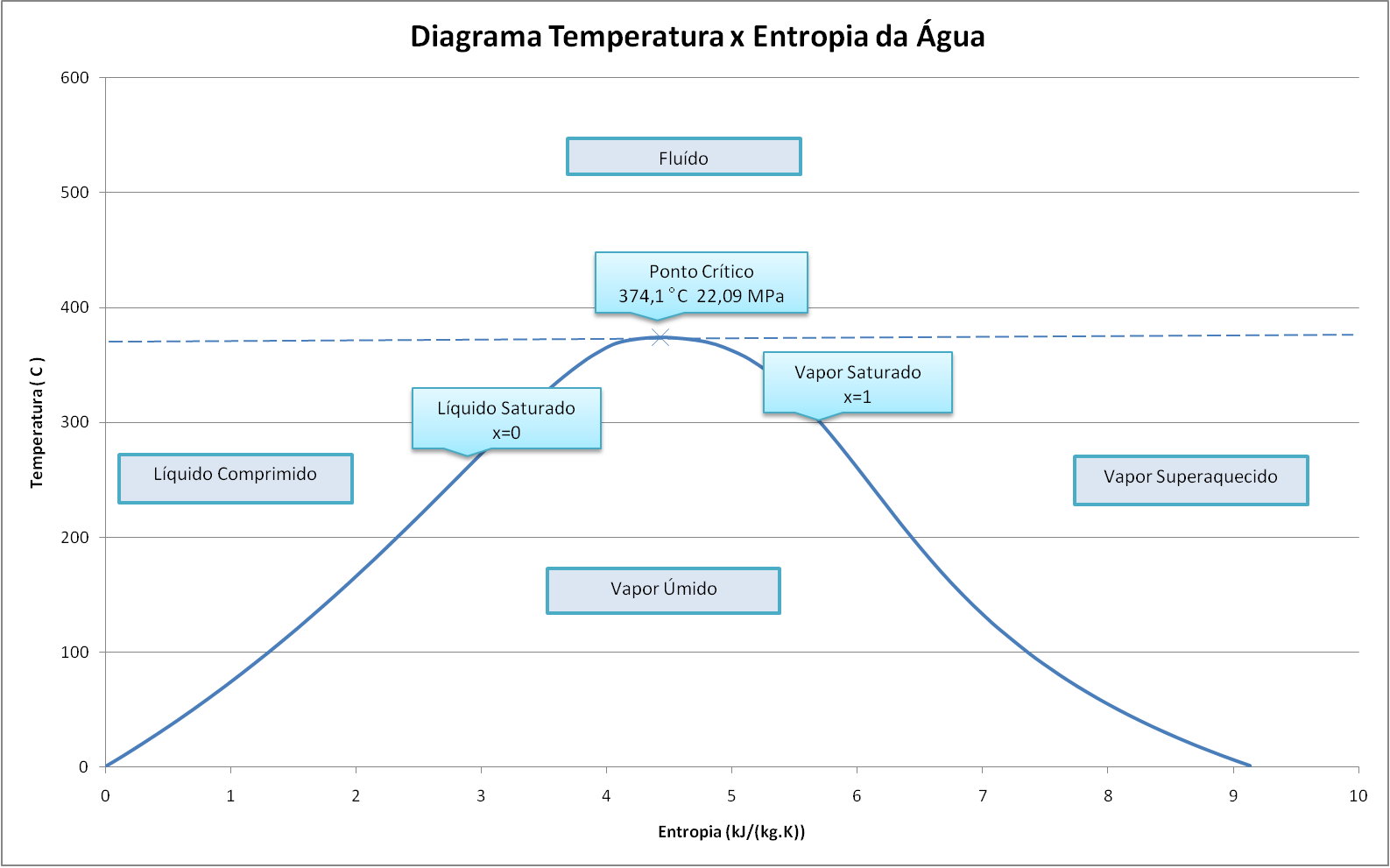
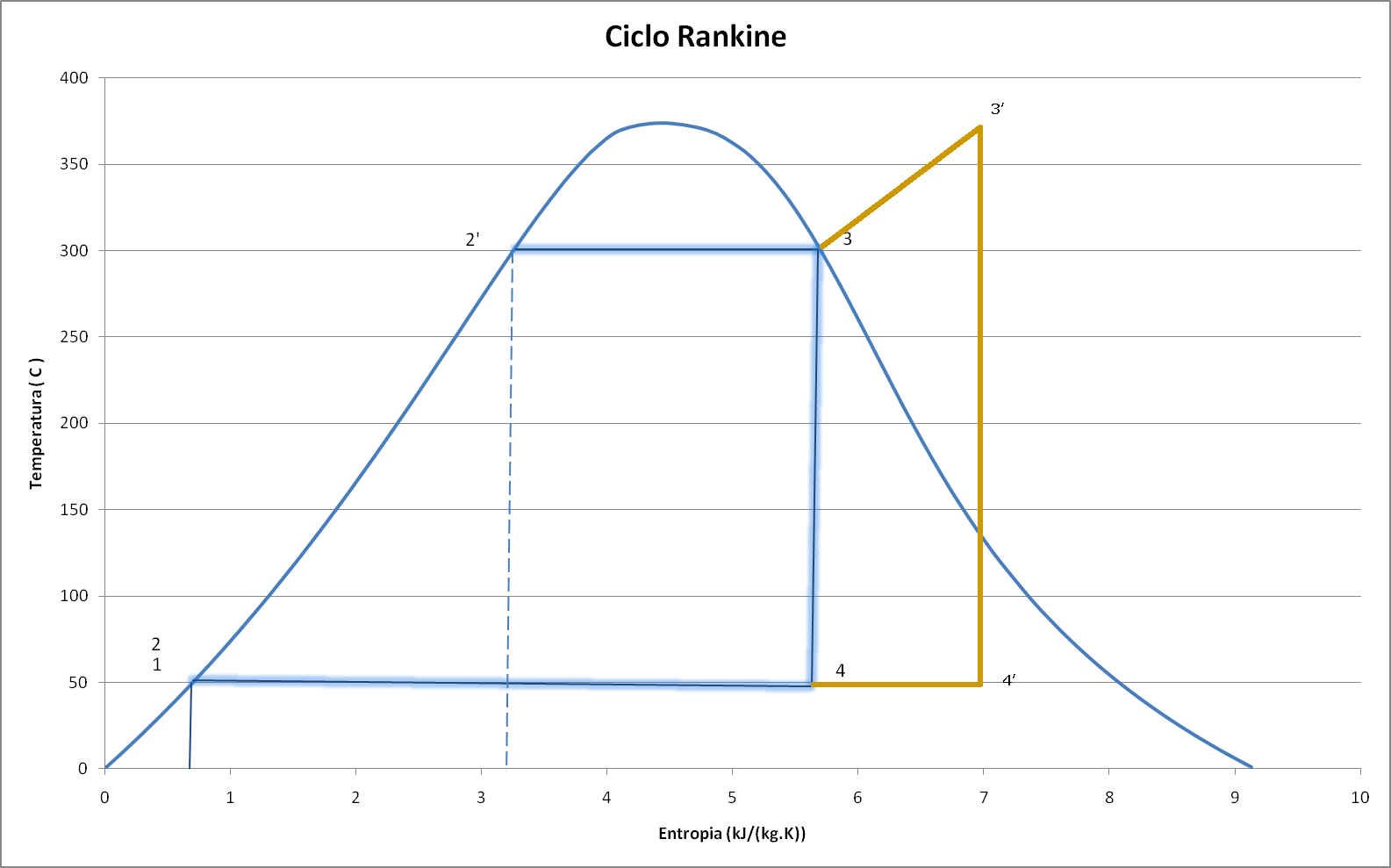
A Figura 3 mostra o diagrama da Temperatura em função da entropia da água.

A curva em azul representa os estados possíveis da água na geração a vapor e no ciclo Rankine.

Entre o condensador e a caldeira, a água se encontra no estado líquido.

Dentro da caldeira, ela passa de líquido para vapor saturado, vapor superaquecido ou fluido dependendo do projeto da caldeira.

Tradicionalmente, as caldeiras trabalhavam abaixo do ponto crítico da água, mas as caldeiras modernas, denominadas de supercríticas, operam acima do ponto crítico.

A região de vapor úmido se caracteriza pela coexistência de água no estado líquido e gasoso. 

Para se caracterizar o estado termodinâmico das substâncias torna-se necessário saber o valor de pelo menos duas variáveis termodinâmicas.

Usualmente, utiliza-se a temperatura e a pressão. Porém, durante a mudança da fase líquida para a gasosa, a temperatura permanece constante e outra grandeza se torna necessária para caracterizar o estado.

Nesses casos, utiliza-se o Título definido como a relação entre a massa de vapor e a massa total, conforme mostra a Equação 2.

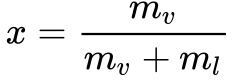
Onde:

• • x é o título [adimensional];
  • m_v é a massa de vapor;
  • m_l é a massa de líquido.

Propriedades da água

Ciclo de Rankine

O Ciclo Rankine consiste no ciclo termodinâmico que melhor representa o processo de geração de energia a partir do vapor d’água.

Contudo, outros fluidos também podem ser utilizados em aplicações especiais, como na geração geotérmica.

O ciclo de Rankine se baseia em quatro processos termodinâmicos:

• • Bombeamento adiabático na bomba – 1 a 2 ^{7 8}
  • Transformação da água em vapor a pressão constante na caldeira – 2 a 3;
  • Expansão adiabática na turbina – 3 a 4;
  • Condensação do vapor a pressão constante no condensador – 4 a 1.

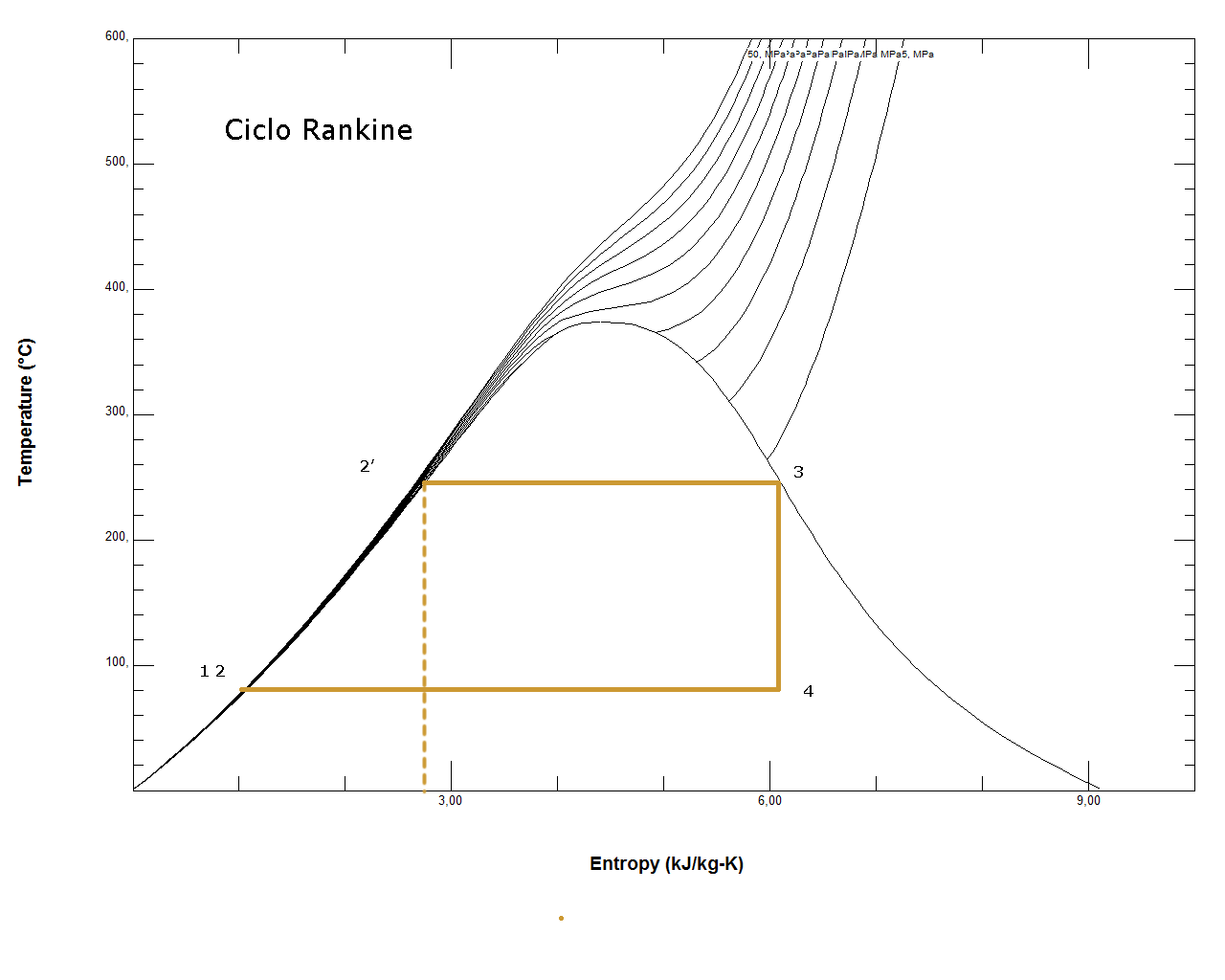
Observa-se que os pontos 1 e 2 são idênticos no diagrama Temperatura x Entropia porque o bombeamento adiabático não produz variação de temperatura nem variação de entropia.

Durante a transferência de calor para a água na caldeira, a temperatura se eleva até o ponto 2´, onde o processo de evaporação se inicia.

A partir deste ponto, a temperatura da mistura água/vapor permanece constante até que todo o líquido tenha se transformado em vapor.

A Equação 3 fornece o rendimento térmico do ciclo Rankine.

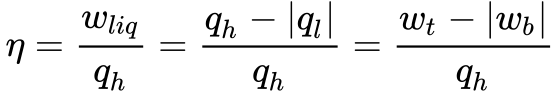
Onde:

• • w_liq é o trabalho líquido executado;
  • q_H é o calor fornecido ao sistema em temperatura elevada;
  • q_L é o calor retirado do sistema em baixa temperatura;
  • w_t é o trabalho realizado pela turbina;
  • w_b é o trabalho realizado pela bomba.

Considerando que:

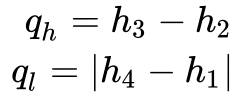
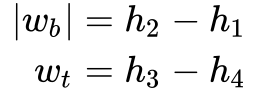
Onde:

• h_i é a entalpia no estado i.

Substituindo as equações 4 e 5 na Equação 3, obtém-se o rendimento térmico do ciclo Rankine em função das entalpias.

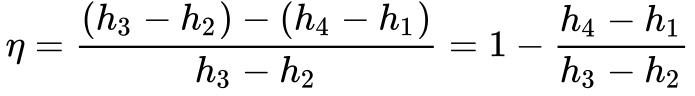
A Equação 6 mostra que o rendimento parece com o rendimento de Carnot, mas a variação de entalpia na caldeira⁹ substituiu a temperatura da fonte quente, e a variação da entalpia no condensador¹⁰ substituiu a temperatura da fonte fria.

Neste ciclo Rankine ideal, a temperatura média de rejeição de calor é constante e igual à temperatura de condensação.

No entanto, a temperatura média de fornecimento de calor na caldeira é inferior à temperatura de vaporização por causa da variação de temperatura entre os pontos 1 e 2′.

Isto significa que o rendimento do ciclo Rankine ideal se torna inferior ao rendimento térmico do ciclo de Carnot operando com temperatura máxima igual a temperatura de vaporização e mínima igual à temperatura de condensação.

O que fazer para aumentar a eficiência do ciclo Rankine?

Basicamente, existem três possibilidades para aumentar o rendimento do ciclo Rankine:

• Redução da pressão na saída da turbina;
• Aumento da pressão no sistema;
• Superaquecer o vapor.

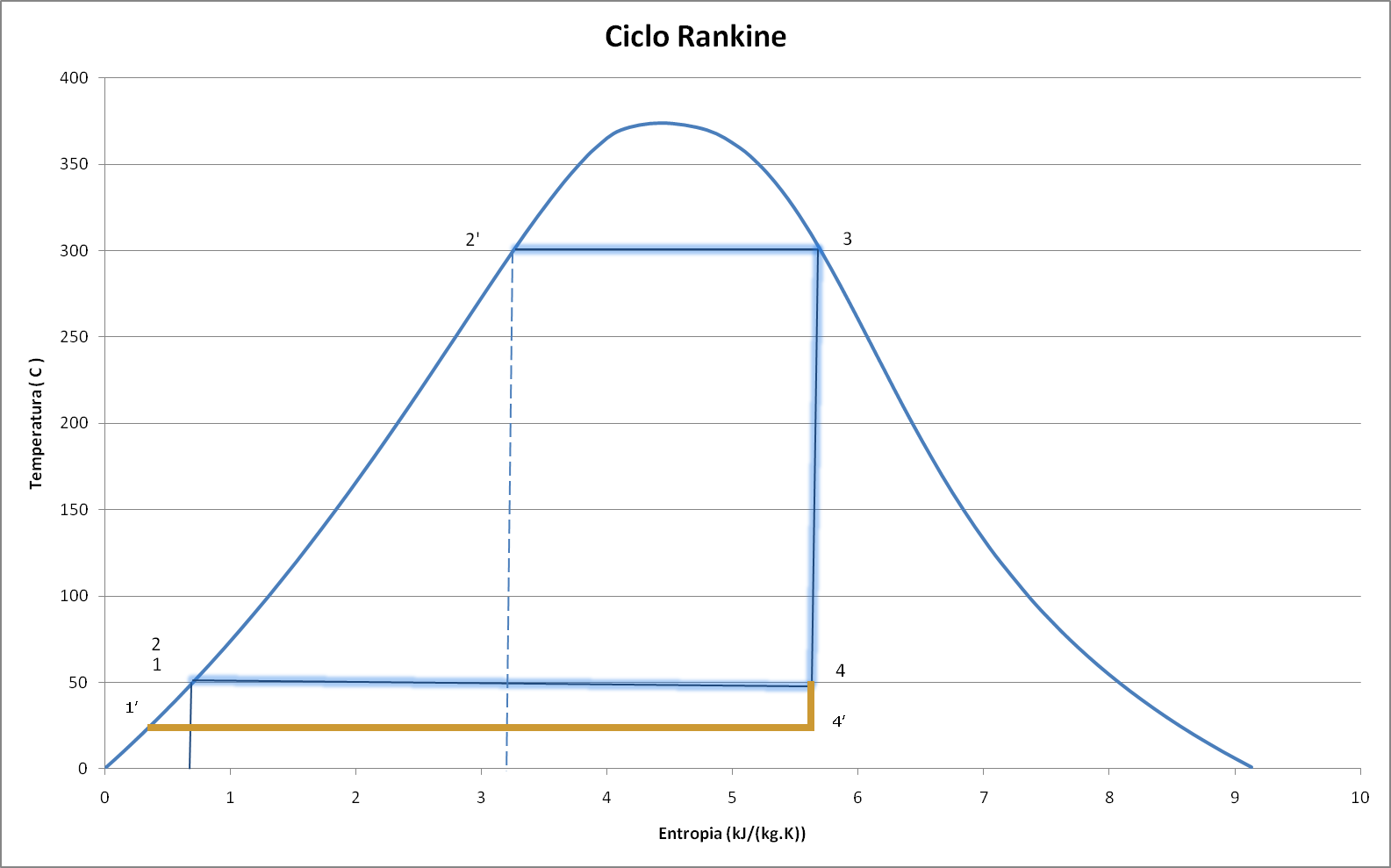
A redução da pressão do vapor na saída da turbina aumenta o rendimento, mas pode provocar condensação do vapor dentro da turbina. Esta água condensada forma gotículas que destroem as palhetas da turbina.

Por isso, o título do vapor na saída da turbina não deve ser inferior a 0,85.

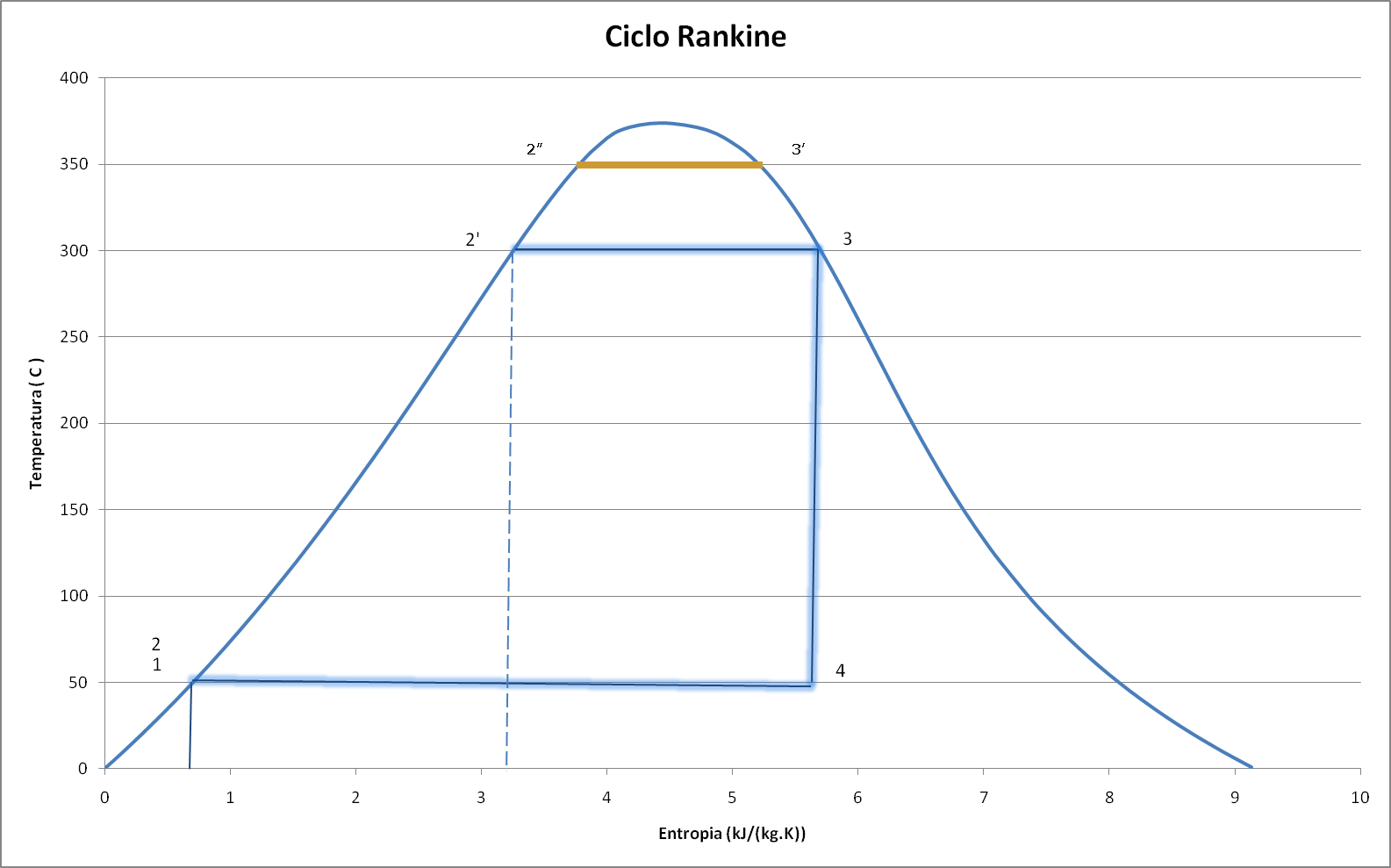
O aumento da pressão na caldeira acarreta aumento de temperatura porque a água passará a ferver numa temperatura mais elevada.

Consequentemente, os esforços termomecânicos no equipamento aumentam, esta solução se encontra limitada pela tecnologia dos materiais existentes.

Finalmente, existe a solução de superaquecer o vapor. Mais uma vez, esta solução deve respeitar as limitações tecnológicas dos materiais disponíveis no mercado.

Na prática, utilizam-se dois sistemas básicos para aumentar a eficiência da geração a vapor:

• • Reaquecimento;
  • Regeneração.

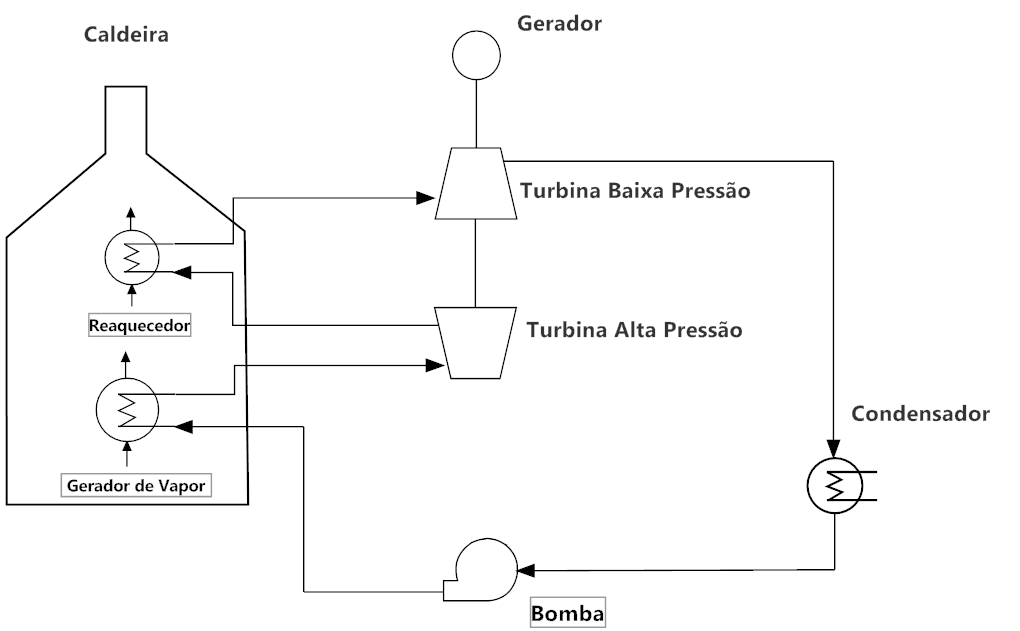
O Reaquecimento consiste em utilizar duas turbinas acopladas ao mesmo eixo e reaquecer na caldeira o vapor da saída da turbina de alta pressão antes de injetá-lo na turbina de baixa pressão conforme mostra a Figura 6.

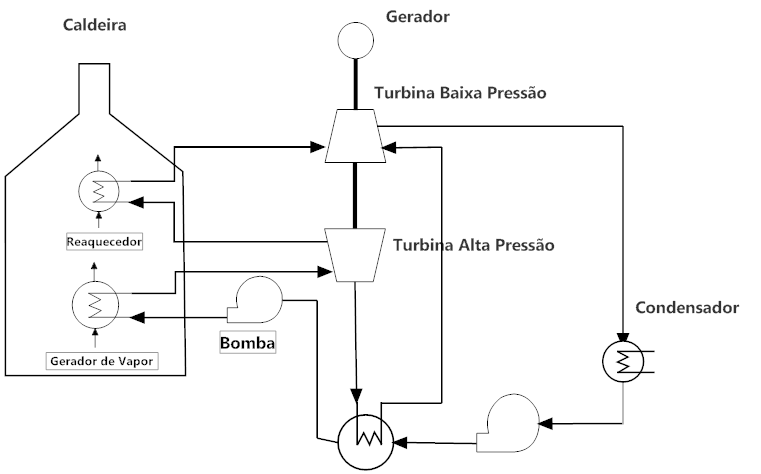
O outro método consiste em pré-aquecer a água de alimentação da caldeira conforme mostra a Figura 7.

 

 

---

Exemplo #1

• Determine o rendimento de um ciclo Rankine da Figura 4, que utiliza água como fluido de trabalho, considerando que:¹¹
  • A pressão no condensador é de 10 kPa;
  • A pressão na caldeira é de 2 MPa;
  • O vapor na entrada da turbina é saturado.
• Determine a temperatura da fonte quente para que a eficiência do ciclo de Carnot fosse igual à eficiência deste exemplo.

Solução

A Equação 6 fornece o rendimento do ciclo Rankine em função das entalpias dos estados termodinâmicos da água no sistema.

Por isso, torna-se necessário calcular o valor da entalpia nos diversos pontos.

A Tabela abaixo apresenta os pontos e as grandezas termodinâmicas fornecidas no enunciado do problema.

O primeiro passo consiste no preenchimento da Tabela.

Para isso, deve-se utilizar Fluid Property Calculator – FPC.

Porém, para determinar o estado termodinâmico necessita-se de duas grandezas termodinâmicas e apenas o primeiro ponto possui a pressão e o título.

1. • Deve-se iniciar utilizando o programa FPC para determinar as grandezas termodinâmicas em #1 porque possui dois valores fornecidos pelo enunciado do problema.
   • Existem três possibilidades para o ponto #2:
     • Considerando o bombeamento adiabático, a Entropia de #2 deverá ser igual à Entropia de #1;
     • Considerando as temperaturas iguais; ¹²
     • O trabalho realizado pela bomba depende do volume específico e da elevação de pressão feita pela bomba. Neste caso, a Equação 7 fornece o trabalho realizado pela bomba ¹³, e a Equação 8 a Entalpia do ponto #2. ¹⁴

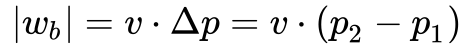
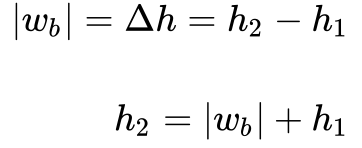
Onde:

• • • • w_b é o trabalho específico realizado pela bomba[J/kg];
      • v é o volume específico [m³/kg];
      • Δp é a variação de pressão na bomba [Pa];
      • h é a entalpia específica [J/kg]
• Na Caldeira, como o sistema não possui perdas, o vapor na saída da caldeira possui as mesmas características da entrada da turbina. Logo, a partir do título =1 e da pressão de 2MPa, pode-se determinar todas as grandezas termodinâmicas de #3 utilizando o programa FPC. 

 

• A partir dos dados obtidos na Tabela acima, pode-se determinar o calor da fonte quente -caldeira, o calor da fonte fria – condensador, e os trabalhos realizados na bomba e turbina.

 

---

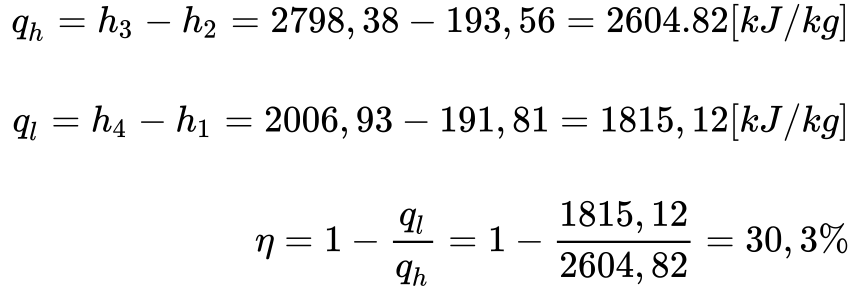
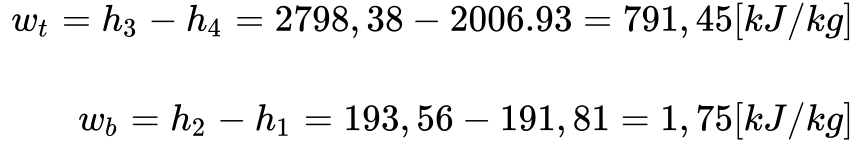
Exemplo #2

Considerando o exemplo anterior, determine:

• • o fluxo de massa necessário para a geração de 1 000MW na turbina;
  • A potência consumida na bomba de alimentação;
  • A potência a ser resfriada pelo condensador;
  • A quantidade de água utilizada no condensador considerando que a temperatura na captação de 20°C e que na saída de 24 °C.

 

Solução

 

• Considerando o trabalho realizado pela turbina igual a 791,45 kJ/kg, o fluxo de massa necessário para gerar 1.000 MW será dado por:

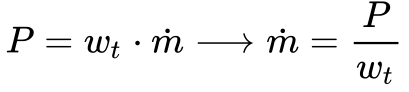
Onde:

• • P é a potência da turbina [kW];
  • w_t é o trabalho específico realizado pela turbina [kJ/kg];
  • m^. é o fluxo de massa de vapor na turbina [kg/s].

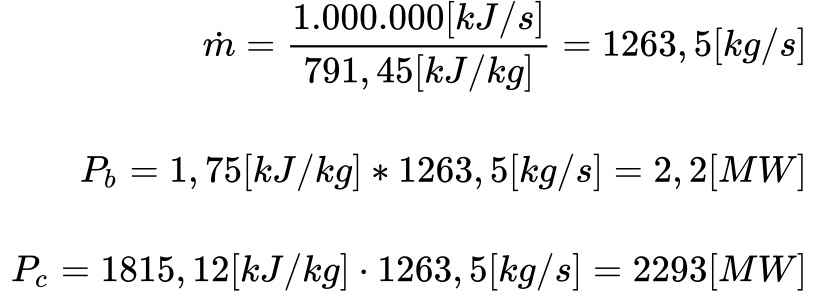
• Considerando o calor específico da água igual a 4,184 [kJ/(kg.K)], a massa de água no trocador de calor será:

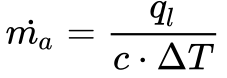
Substituindo os números na Equação 9, deve-se utilizar que 137 toneladas de água por segundo para resfriar o vapor na saída da turbina.

---

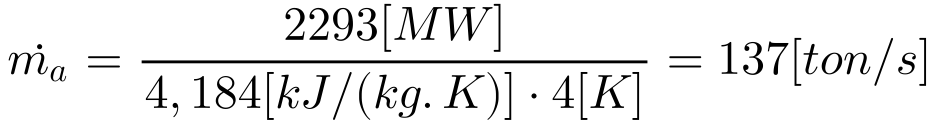
Comentários sobre os Exemplos

A bomba de alimentação da usina a vapor consome parcela significativa da potência gerada.

Isto vale para toda geração a vapor, independentemente, do combustível utilizado.

Motores elétricos acionam essas bombas e, no caso de falta de energia para alimentá-las, as consequências podem ser catastróficas, como em Fukushima e Chernobyl.

Neste exemplo, a potência para a bomba de alimentação foi de 2,3 MW, que representa 0,25% da potência nominal da usina.

Consequentemente, pelo menos dois geradores de emergência de 2,5 MW deveriam existir nesta usina, o que representa um investimento adicional considerável. 

Denomina-se de black-start quando esses geradores possuem a capacidade de alimentar todos os serviços auxiliares fundamentais da usina de forma que ela possa partir mesmo sem a energia do sistema.

Referências

• BORGNAKKE, C., SONNTAG, R.E., Fundamental of Thermodynamics, 8 ed., Wiley, 2013.
• LORA, E., ROSA DO NASCIMENTO, M.A. (Coord.) Geração Termelétrica – Planejamento, Projeto e Operação. Vol.1. Interciência. 2004.¹⁵
• LORA, E., ROSA DO NASCIMENTO, M.A. (Coord.) Geração Termelétrica – Planejamento, Projeto e Operação. Vol.1. Interciência. 2004 ¹⁶
• POTTER, M. SOMERTON, C. D., Schaum’s Outline of Thermodynamics for Engineers, McGraaw-Hill, 2010.