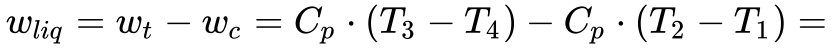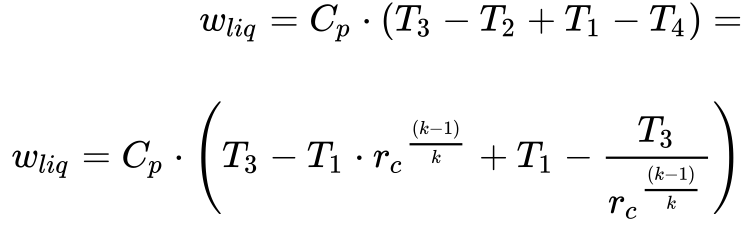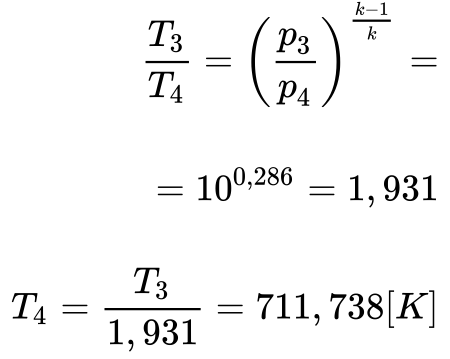“Claramente, existem muitos lugares onde o diesel é o rei ou a turbina a gás é o rei, ou os motores CI vencerão, mas há muitos lugares no mundo onde, como vimos, eles simplesmente não farão o trabalho. A versão moderna do motor Stirling tem algumas características muito, muito atraentes, e estamos tentando otimizá-la para algumas dessas aplicações.“
O desenvolvimento das turbinas a gás começou paralelamente ao desenvolvimento do motor a vapor. A primeira patente relativa ao antecessor da moderna turbina a gás foi concedida em 1791.
No entanto, a turbina a vapor se difundiu no mercado enquanto a turbina a gás enfrentou problemas tecnológicos decorrentes da falta conhecimentos sobre aerodinâmica, necessários para o projeto de compressores eficientes, e decorrentes da inexistência de materiais adequados para resistir às altas temperaturas.
Somente a partir da década de 30, a turbina a gás se tornou um produto comercial impulsionada pela indústria aeronáutica em desenvolver propulsão com menor relação peso/potência.
Atualmente, as turbinas a gás são classificadas, de acordo com a aplicação, em:
-
- Industriais;
- Aeroderivativas.
As turbinas industriais são mais robustas e podem ser encontradas com potências entre 10 kW e 350MW.
Quando comparadas com as turbinas aeroderivativas, as turbinas industriais apresentam as seguintes características:
-
- Mais pesadas;
- Mais robustas;
- Menos eficientes;
- Menor taxa de compressão;
- Maior temperatura de exaustão maior;
- Manutenção mais simples;
- Mais baratas;
Exemplos: Solar, GE Frame, Como Funciona.
Conforme o nome já diz, as turbinas a gás aeroderivativas se baseiam nas turbinas de avião.
Quando comparadas com as turbinas industriais, as aeroderivativas apresentam as seguintes características:
-
- Mais leves;
- Mais barulhentas;
- Mais eficientes;
- Maior taxa de compressão;
- Menor temperatura de exaustão;
- Manutenção mais complexa e na fábrica;
- Mais caras;
Exemplo: GE LM series.
Com relação aos aspectos construtivos, as turbinas a gás se classificam em:
-
- Eixo Simples;
- Eixo Duplo;
- Compressor Dual;
- Regenerador;
- Resfriador Intermediário;
Funcionamento das Turbinas Gás
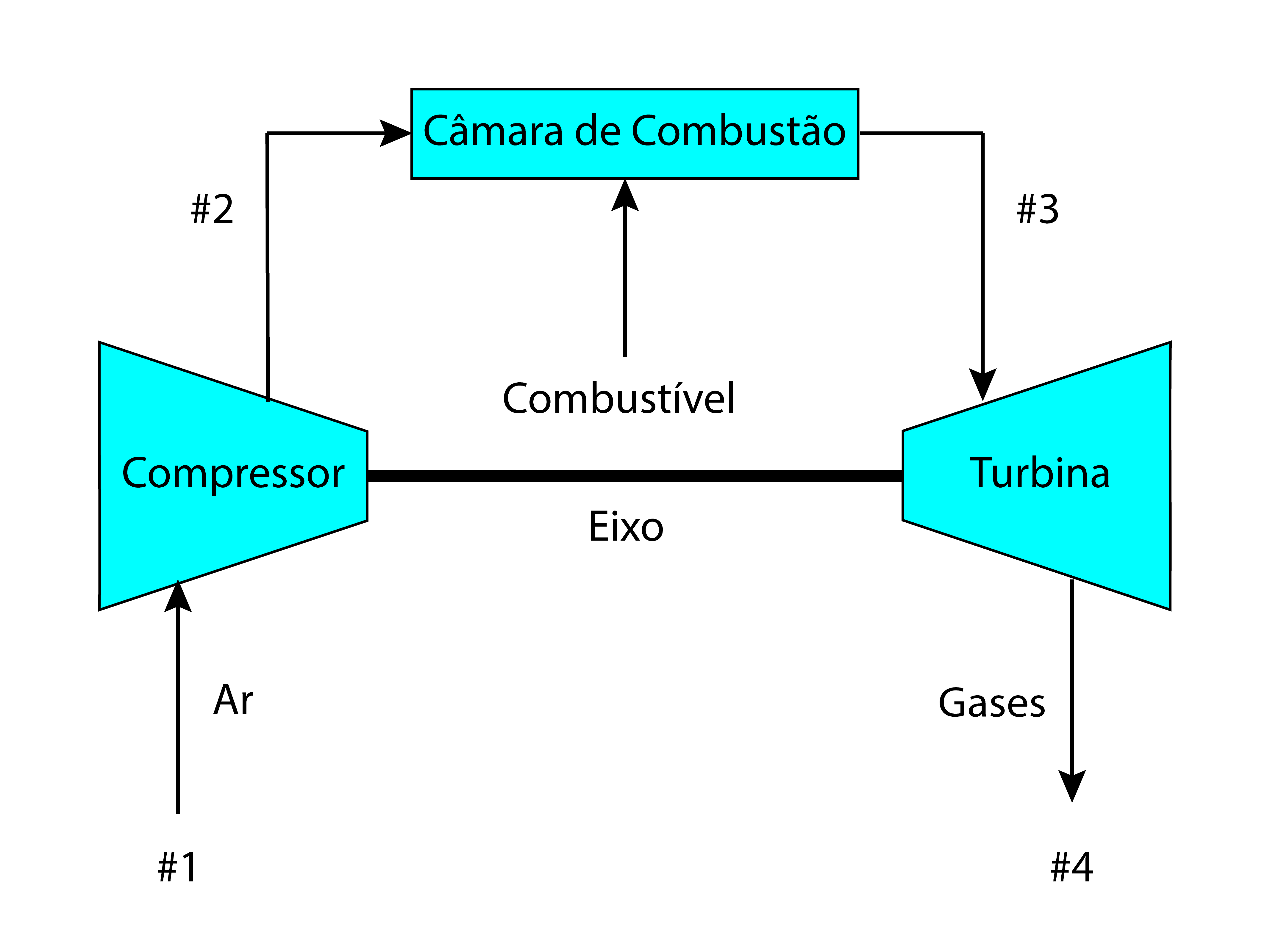
Toda turbina a gás consiste basicamente em um compressor, uma câmara de combustão e uma turbina, conforme mostra a Figura 1.
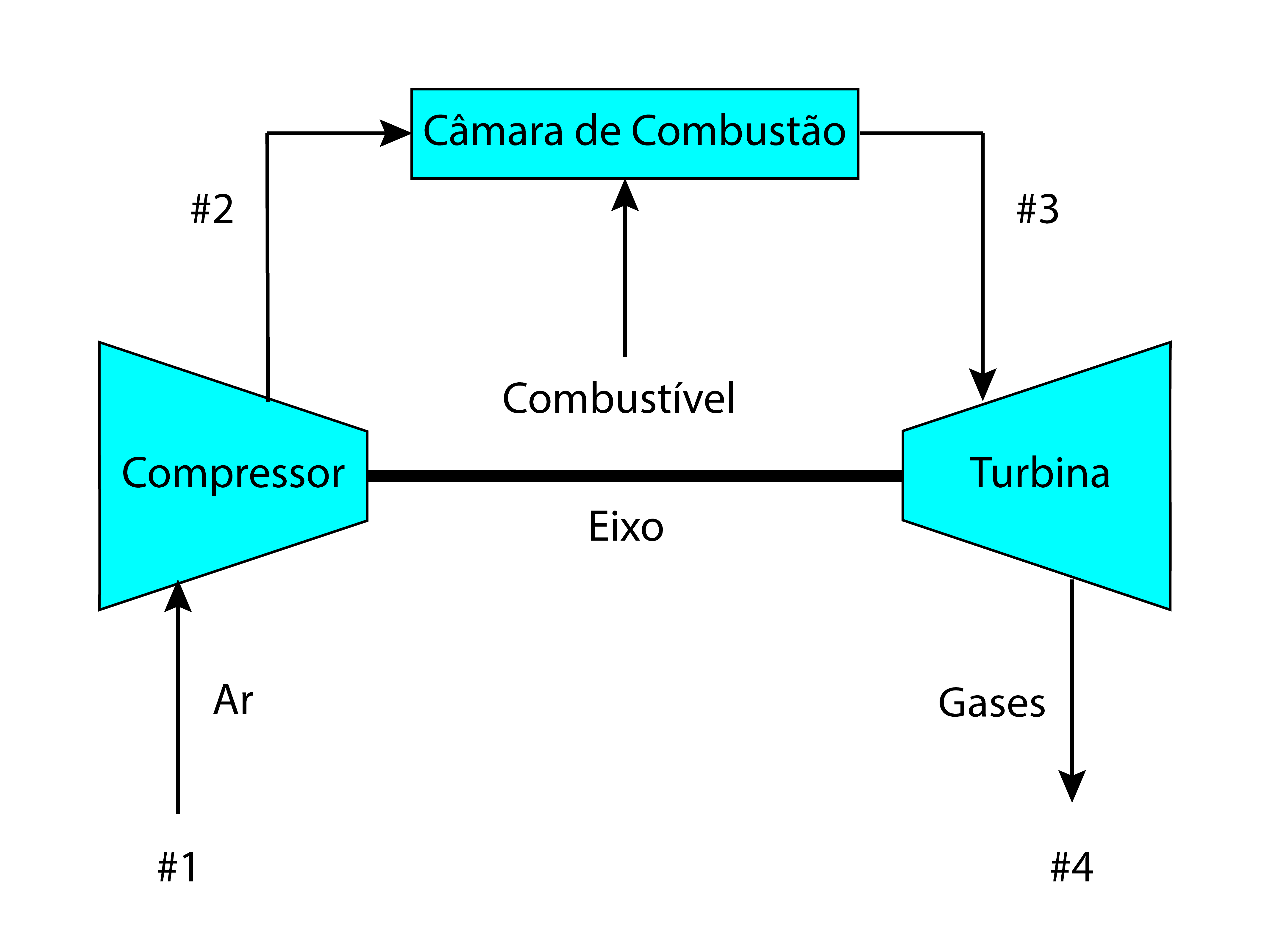
O compressor eleva a pressão do ar entregue à câmara de combustão utilizando parte do trabalho mecânico da turbina.
Por sua vez, o combustível queimado na câmara de combustão fornece energia em temperatura elevada.
Estes gases aquecidos entram na turbina e se expandem realizando trabalho mecânico, que aciona o compressor e a carga.
Finalmente, os gases da saída da turbina fluem para a atmosfera que os esfria.
Ciclo Brayton
Considerando a turbina a gás como sendo uma máquina térmica ideal, a Figura 2 mostra os quatro processos envolvidos no seu funcionamento:
-
- Compressão Isentrópica, 1-2;
- Adição de calor a pressão constante, 2-3;
- Expansão Isentrópica, 3-4;
- Retirada de calor a pressão constante, 4-1.
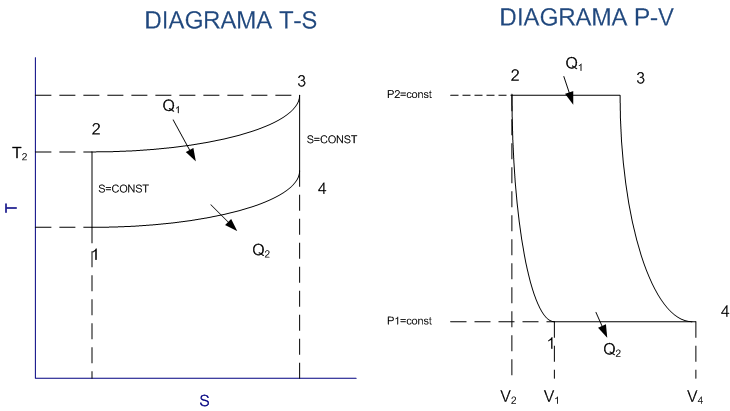
Este ciclo se assemelha ao ciclo de Rankine porque possui duas etapas isentrópicas e duas isobáricas.
Porém, a grande diferença consiste no fluído de trabalho e seu estado. No ciclo Rankine o fluído de trabalho – água- muda de fase, mas na turbina a gás o fluído de trabalho – ar e gases da combustão – se mantém no estado gasoso todo o tempo.
Denomina-se este ciclo termodinâmico de ciclo Brayton, que considera as seguintes hipóteses:
-
- O fluído de trabalho é um gás perfeito com calor específico e composição constantes;
- Os processos de compressão e expansão são reversíveis, isentrópicos e adiabáticos;
- As parcelas de energia cinética são desprezíveis;
- Não existem perdas de pressão;
- O fluxo de massa é constante em todo o ciclo;
- O processo de combustão é representado por um processo de transferência de calor a partir de uma fonte quente;
- O ciclo se completa através da transferência de calor para o meio ambiente – a fonte fria;
- Todos os processos são reversíveis;
Portanto, pode-se aplicar os conceitos básicos desenvolvidos no Capítulo de Geração a Vapor.
A Equação 1, apresentada no Capítulo Geração a Vapor, fornece a eficiência do ciclo.
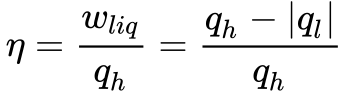
Onde:
-
- η é o rendimento;
- wliq é o trabalho líquido realizado pela máquina;
- qh é o calor fornecido pela fonte quente;
- ql é o calor fornecido pela fonte fria;
Contudo, como o fluido de trabalho se encontra sempre na fase gasosa e o considerando um gás ideal com Calor Específico constante, a Equação 2 fornece o rendimento em função das entalpias.
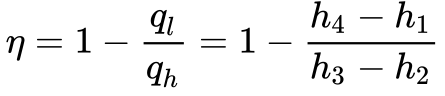
Onde:
-
- hi é a entalpia específica no ponto i;
De acordo com a termodinâmica e considerando o calor específico constante, a variação de entalpia depende apenas da diferença de temperatura e do calor específico do fluido de trabalho, conforme mostra a Equação 3.
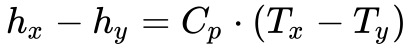
Onde:
-
- Cp é o calor específico a pressão constante.
Substituindo a Equação 3 na equação 2, obtém-se a seguinte expressão:
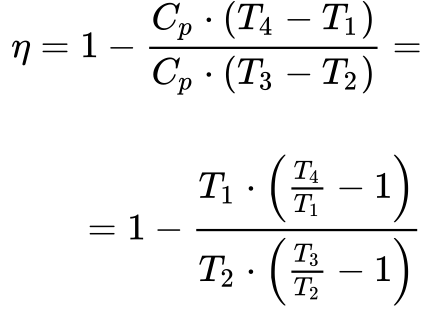
Como as pressões de admissão e exaustão da turbina se igualam à pressão atmosférica, a queda de pressão na turbina deve se igualar ao aumento de pressão no compressor. 1 Desta maneira, a taxa de compressão na turbina será dada pela Equação 5.
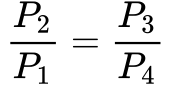
A Equação 6 fornece a variação de entropia no compressor para gases ideais.
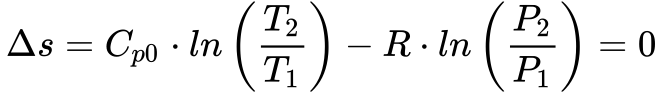
Rearrumando a Equação 6, obtém-se a relação entre as relações de pressão e temperatura no compressor.
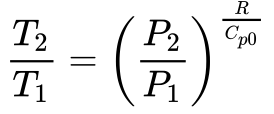
A Equação 8 apresenta a relação entre a constante dos Gases – R – e o Calor Específico a Pressão Constante de um gás ideal – Cp0.
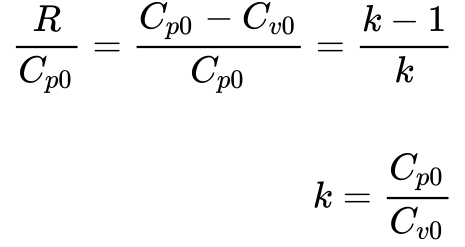
Onde:
-
- R é a constante universal dos gases;
- Cp0 é calor específico a pressão constante;
- Cv0 é o calor específico a volume constante.
A partir da Equação 7, obtém-se-se a relação entre temperatura e pressão na turbina considerando o ar um gás ideal. 2
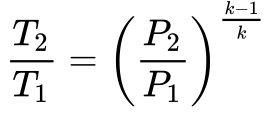
A partir das Equações 9 e 5, mostra-se que T3/T2=T4/T1.
Substituindo esta relação na Equação 4, obtém-se o rendimento da turbina a gás a partir apenas das pressões P1 e P2 de acordo com a Equação 10.
Observa-se que esse rendimento depende apenas da relação de compressão do compressor. Quanto maior a taxa de compressão, maior o rendimento.
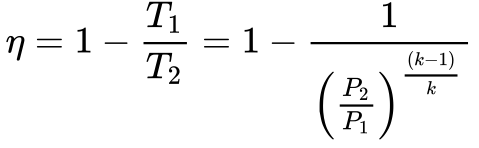
A Equação 11 apresenta o trabalho no compressor e na turbina.
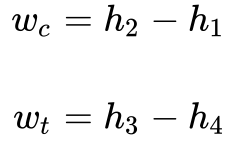
Substituindo a Equação 3 na Equação 11, obtém-se a Equação 12.
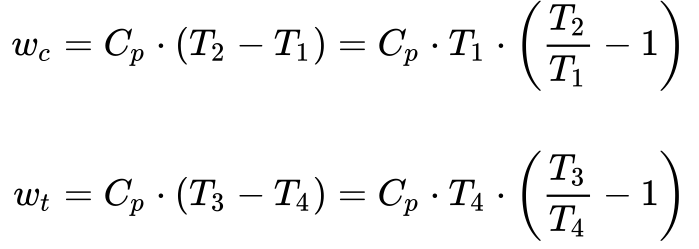
Substituindo a Equação 9 na Equação 12, obtém-se a Equação 13.
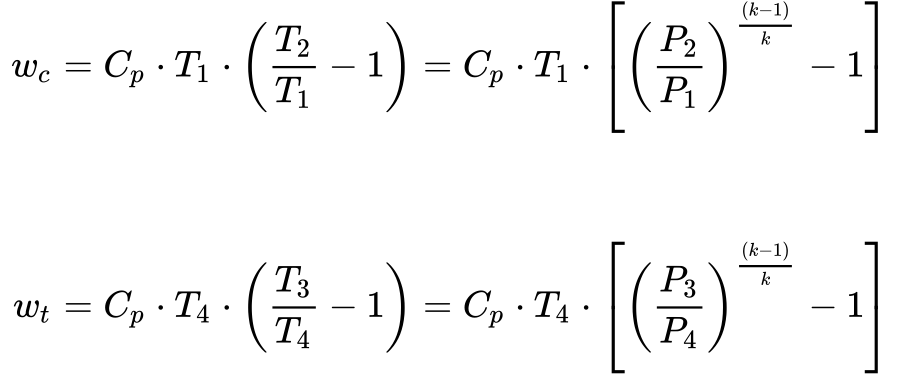
Substituindo a Equação 5 na Equação 13, obtém-se a seguinte expressão:
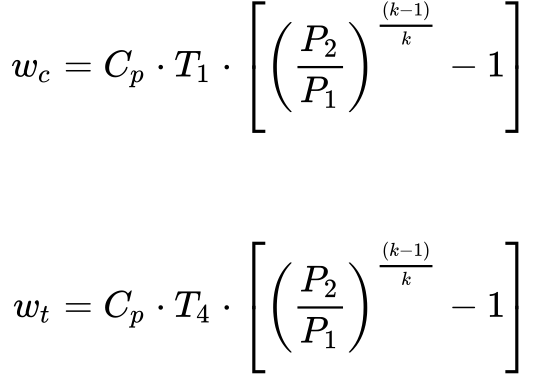
Por isso, o projeto das turbinas a gás apresenta dois parâmetros básicos:
-
- a taxa de compressão – rc;
- e coeficiente de temperatura – t.
A Equação 15 fornece a definições desses parâmetros.
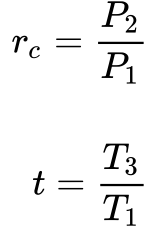
Onde a taxa de compressão consiste na relação entre a pressão na saída e na entrada do compressor e o coeficiente de temperatura na relação entre a temperatura na saída da câmara de combustão e a temperatura do ar na entrada do compressor, em graus Kelvin.
As turbinas aeroderivativas apresentam taxa de compressão entre 20 e 30 e o coeficiente de temperatura entre 5 e 5,5.
Em todos os casos, a temperatura máxima se limita à suportabilidade térmica dos materiais utilizados, que hoje se encontra na ordem de 1 500 °C.
Utilizando a Equação 15 e a Equação 14, calcula-se o trabalho líquido disponibilizado pela turbina da seguinte maneira:
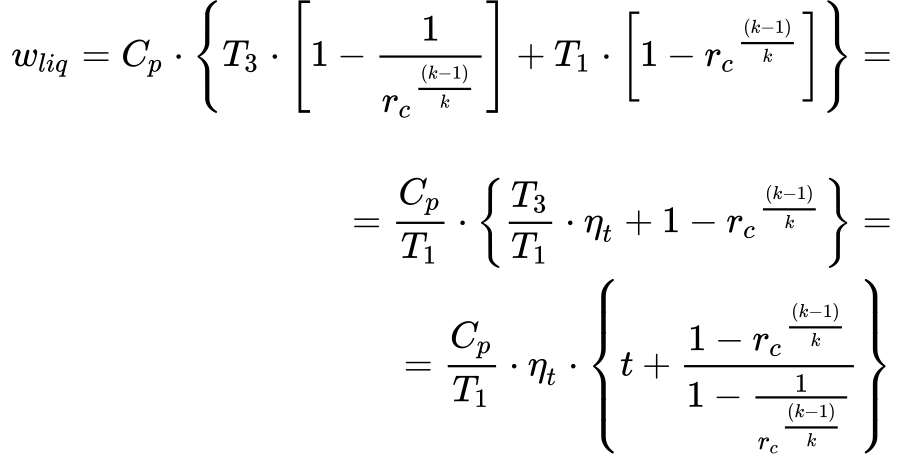
O segundo termo da Equação 16 requer simplificação algébrica conforme a Equação abaixo.
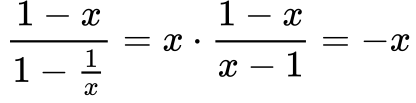
Aplicando a simplificação da Equação 17 na Equação 16, obtém-se a Equação 18, que determina o trabalho líquido disponibilizado pela turbina e o rendimento.
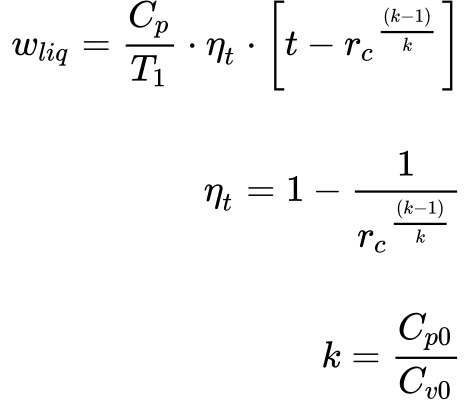
Onde:
-
- Cp é o calor específico a pressão constante;
- Cv é o calor específico a volume constante;
- ηt é o rendimento térmico;
- wliq é o trabalho líquido
Deve-se observar que o rendimento depende apenas da relação de pressão e do calor específico e o trabalho depende também da relação de temperatura.
Estas expressões foram deduzidas considerando calor específico constante e o gás ideal.
Conforme mostra a Figura 3, o calor específico do ar não pode ser considerado constante entre a temperatura ambiente e a temperatura máxima da turbina. Esta variação, de aproximadamente 16%, tem algum impacto nas análises anteriores.
Figura 3. Calor específico do ar.
Exemplo #1
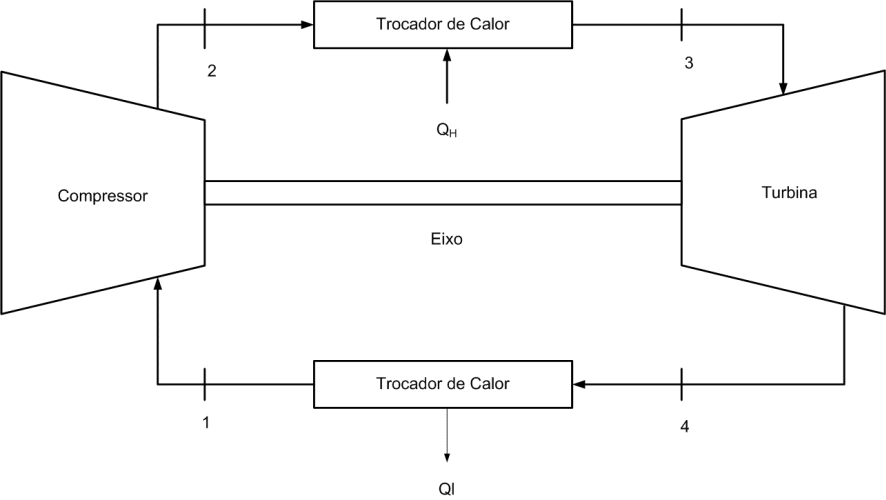
Considerando a Figura 4, o ar entra no compressor da turbina a gás com pressão de 0,1 Mpa e temperatura de 15 °C.
O compressor fornece ar comprimido a 1Mpa e a temperatura máxima na câmara de combustão é de 1100 °C.
Determine as seguintes grandezas analisando de acordo com as hipóteses do ciclo Brayton:
-
- A temperatura e pressão em todos os pontos do ciclo;
-
O trabalho no compressor e na turbina;
-
O rendimento do conjunto.
Solução
Por se tratar de processo isoentrópico, a Equação 3 fornece a relação entre as temperaturas na saída do compressor e a temperatura do ar – pontos 2 e 1.
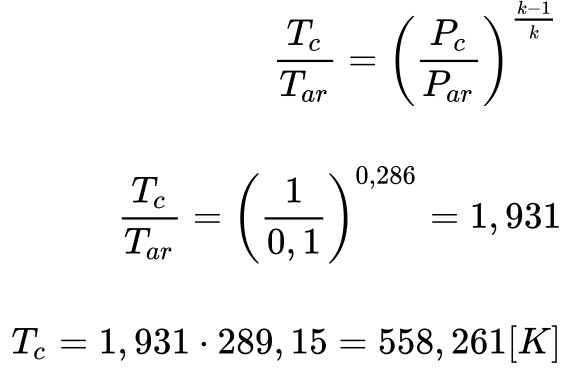
A variação da entropia entre os estados 1 e 2 fornece o trabalho realizado pelo compressor.
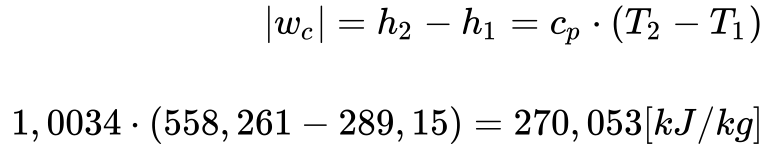
Por sua vez, a Equação 5 determina o trabalho realizado pela turbina.
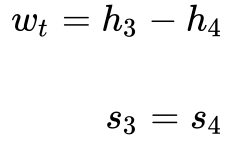
Desta maneira, a Equação 6 determina a temperatura e o trabalho na saída da turbina.
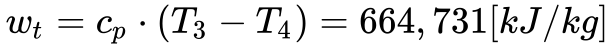
O compressor utiliza parte deste trabalho gerado pela turbina e a Equação 7 fornece o trabalho mecânico líquido disponível para o gerador.
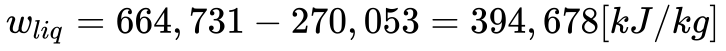
O ciclo se completa com o resfriamento dos gases de escape da turbina na atmosfera. Desta maneira, a Equação 8 determina o calor rejeitado.
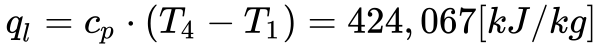
Finalmente, determina-se o rendimento térmico do sistema. Para isso, deve-se calcular a quantidade de calor injetado na turbina. Considerando o sistema ideal, a Equação 9 fornece o calor injetado na turbina.
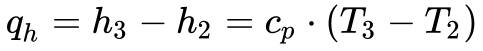
Finalmente, a Equação 10 calcula o rendimento térmico da turbina.
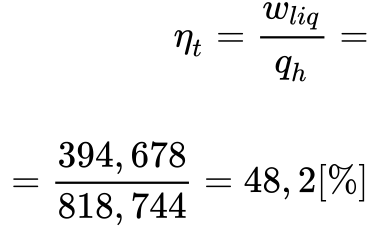
Obtém-se esse mesmo valor através da Equação 2.