Vazão

A potência, coforme apresentado no capítulo Hidrelétricas depende da vazão de água que movimenta suas turbinas – a vazão turbinada.

A vazão representa a quantidade de água escoada superficialmente por unidade de tempo, sendo medida em determinados pontos ou calculada a partir dos modelos hidrológicos.

Denomina-se de vazão afluente¹ a vazão que chega a um determinado ponto ou usina.

As usinas hidrelétricas não transformam toda a vazão afluente em energia. Parte da água se transforma em vapor pela evapotranspiração, parte é vertida sem passar pelas turbinas, e parte se transforma em volume útil do reservatório.

A divisão entre estas parcelas depende da operação do reservatório e do Balanço Hídrico.  

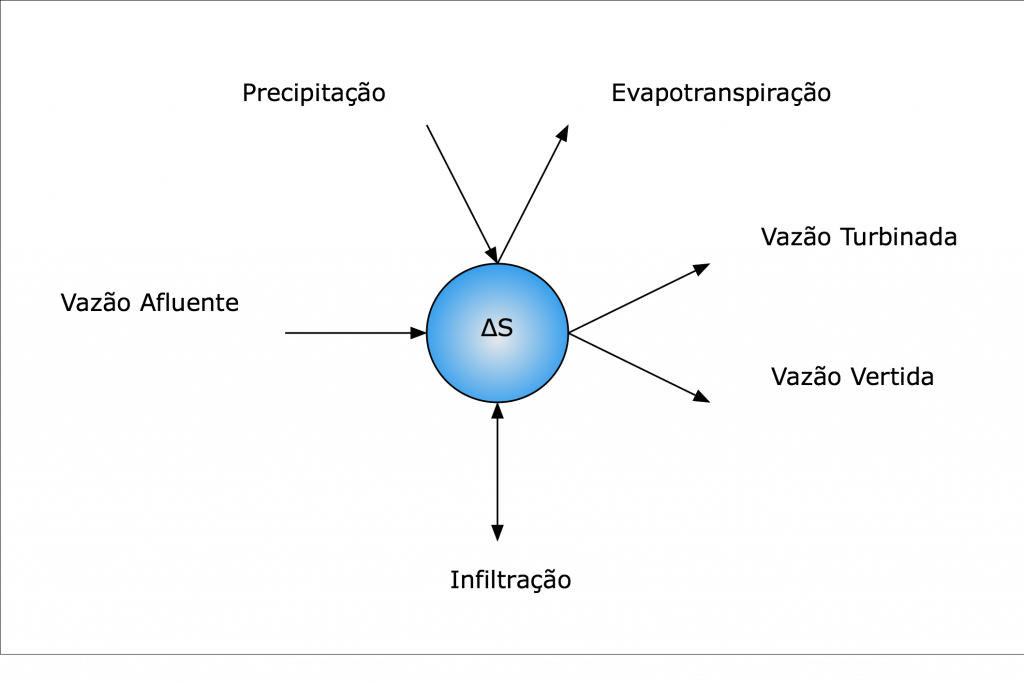
Além disso, em alguns poucos casos existe a vazão transferida e a vazão de outras estruturas.

A vazão afluente depende das condições hidrológicas naturais da bacia hidrográfica, dos aproveitamentos existentes a montante e de outros usos da água ao longo da bacia hidrográfica.

Mede-se a vazão em diversos pontos dos rios das diversas bacias hidrográficas. A Agência Nacional de Águas – ANA – disponibiliza as informações da rede de estações de coleta de dados.

Independentemente do tipo de vazão, as séries das medições de cada ponto formam um conjunto ou série de dados horários, diários ou mensais.

Denomina-se este tipo de série de Série Temporal, que forma um capítulo especial na matemática.

Analisar os dados das séries históricas de vazão requer alguns cuidados. Trabalhar com os dados brutos destas medidas torna-se inadequado porque a atividade humana ao longo das bacias hidrográficas altera o valor das vazões de forma artificial. Por exemplo, a construção de uma represa, afeta a vazão do rio a jusante mesmo que o regime hidrológico da bacia não tenha mudado. Por isso, as séries de vazão medidas são processadas e transformadas nas séries de vazão natural afluente. Teoricamente, esta nova série de vazões equivale à série histórica de vazões que existiria se não houvesse nenhuma intervenção humana.

O ONS fornece relatórios anuais com os dados de medições mensais e diárias das vazões naturais de todas as usinas em operação a partir de 1931. A obtenção, manipulação e consolidação dessas informações encontra-se descrita nos Procedimentos de Rede do ONS. A questão da medição e manipulação de dados hidrológicos foge do escopo deste curso. Por isso, vamos considerar como premissa que os dados de vazão natural afluente disponibilizados pelo ONS estão corretos.

Análise da Vazão

Como o volume de dados é muito grande, a análise dos dados de vazão requer metodologias e ferramentas mais sofisticadas. Planilhas eletrônicas, tipo Excel e Numbers, atingem seus limites com os dados de vazão e não possuem funções avançadas de estatística para tratar séries temporais. ²

Como exemplo, escolhemos Três Marias para esta análise porque ela incorpora características do comportamento hidrológico dos três maiores sistemas – SE/CO, N e NE – e possui reservatório de acumulação.

A Figura 1 mostra a vazão natural afluente média diária de 1 de janeiro de 1931 a 31 de dezembro de 2018 da usina de Três Marias. Pouca ou nenhuma informação pode ser retirada desta figura sem um tratamento mais elaborado dos dados. Porém, verifica-se que existem muitas variações nos 88 anos de dados.

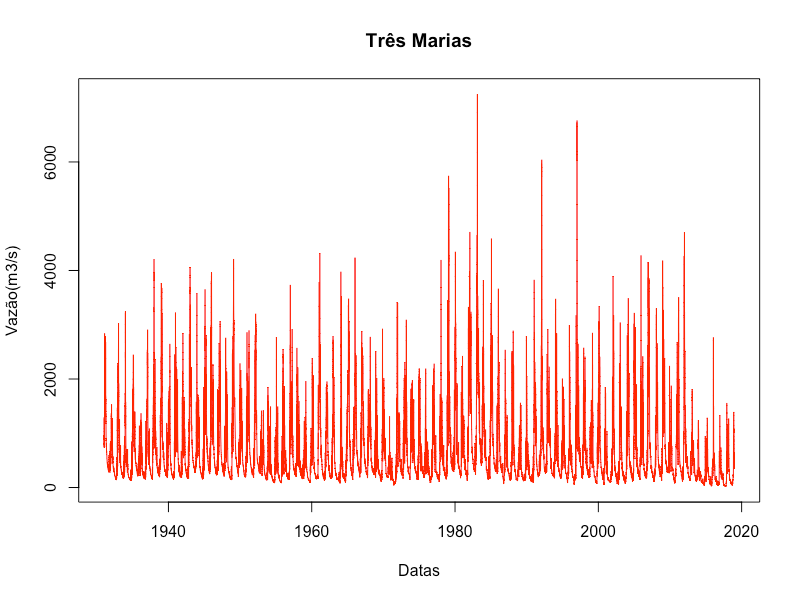
Normalização da Vazão

Trabalhar com os dados de vazão em m³/s apresenta inconvenientes na comparação com outros rios e aproveitamentos. A normalização resolve este problema, mas a escolha da base para esta normalização requer análise. Consideramos a média de longo prazo – MLT – como sendo a base mais adequada.

A Figura 2, que representa a série temporal da vazão natural afluente normalizada de Três Marias, diferencia-se da Figura 1 apenas pela a escala de vazão. ³

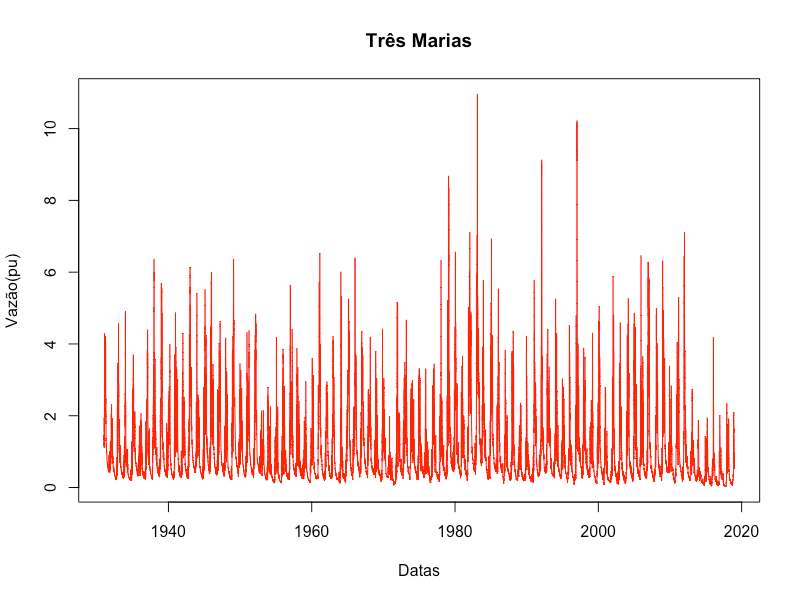
Sumário Estatístico da Vazão

A análise das vazões inicia-se com o Sumário Estatístico porque agrega diversos índices estatísticos que fornecem uma visão geral do comportamento dos dados. A tabela abaixo apresenta o sumário de Três Marias. Observa-se que alguns índices são adimensionais e outros não. A Curtose e a Assimetria exemplificam os índices adimensionais e os demais possuem dimensão. A segunda coluna apresenta os mesmos parâmetros estatísticos normalizados pela média. Com esta normalização, todos os índices tornam-se adimensionais e torna-se mais fácil comparar diferentes usinas.

A Tabela abaixo, que apresenta o sumário estatístico das séries de vazão natural afluente de Três Marias diárias e mensais, mostra que a média permanece praticamente constante e independe da amostra estatística da série temporal. Por isso, utilizamos a média como base na normalização das séries temporais. 

A Curtose mede o peso estatístico dos extremos da distribuição de probabilidade de uma variável aleatória. Quando maior a Curtose, maior a probabilidade de ocorrência de valores extremos.

A Mediana representa o ponto de probabilidade acumulada de 50%. A mediana de 403 m³/s significa que 50% do tempo a vazão natural afluente desta usina encontra-se abaixo deste valor ou superior a este valor. Erro muito comum consiste em considerar a média como sendo o índice que divide a distribuição de probabilidade em partes iguais. Isto somente ocorre com distribuições de probabilidade simétricas. Por isso, a assimetria também pode ser avaliada pela diferença entre a média e a mediana.

Os valores Máximo e Mínimo estabelecem os valores extremos observados na amostra dos dados.  ⁴

Três Marias

Histograma da Vazão

A Figura 3 apresenta o histograma da vazão natural afluente diária normalizada pela média da usina de Três Marias com alguns valores do sumário estatístico indicados. Observa-se que a distribuição de probabilidade da vazão apresenta Assimetria positiva e, por isso, a moda e a mediana são menores do que a média. Esta característica ocorre com todas as hidrelétricas e decorre do fato das vazões possuírem valor mínimo de zero. ⁵

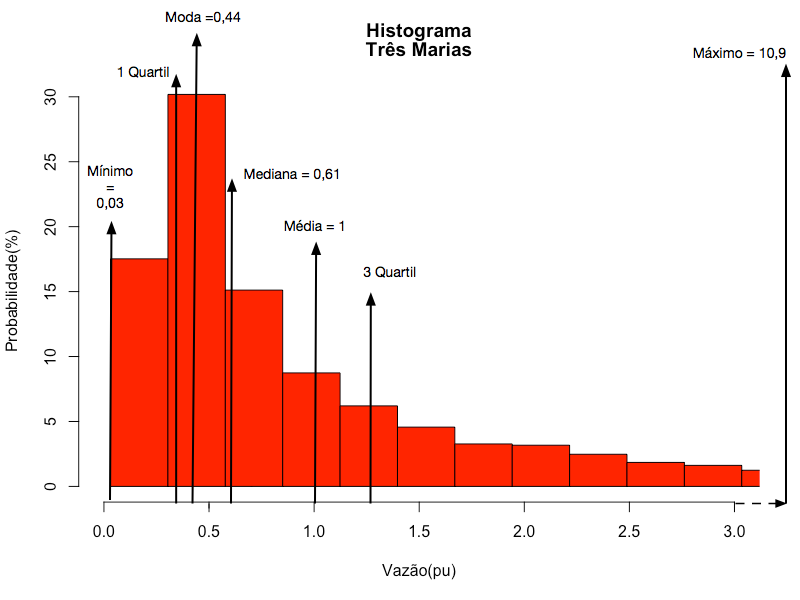
Boxplot da Vazão

A figura 4 apresenta o Boxplot⁶, da vazão natural afluente mensal da usina de Três Marias.

Este tipo de gráfico torna-se extremamente útil para visualização rápida dos dados. ⁷ Observa-se claramente a variação anual da vazão com o período úmido entre novembro e abril. Entre maio e outubro as vazões encontram-se abaixo da média.

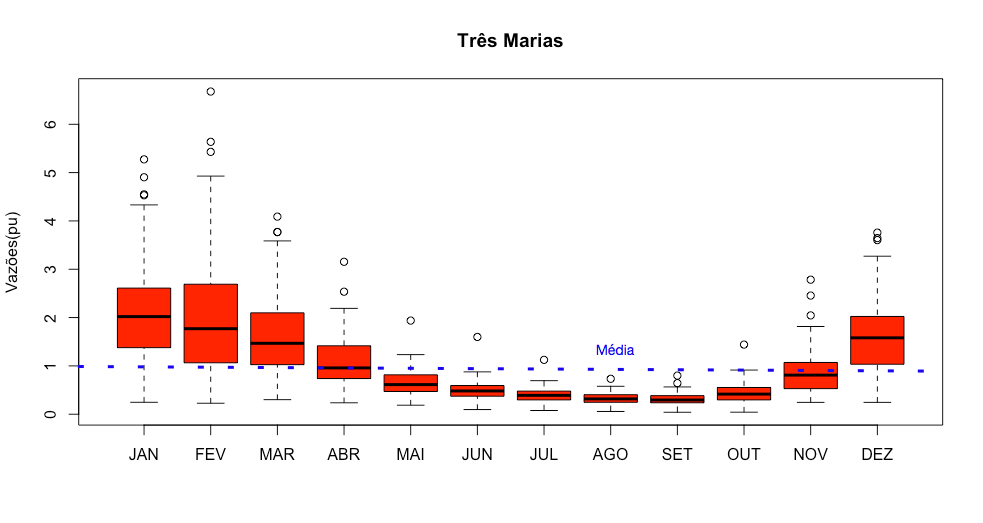
Conforme mostrado no capítulo de revisão estatística, os valores mais extremos correspondem ao mínimo e ao máximo da série. Os valores extremos da caixa representam as vazões com probabilidade de 25% e 75%. Portanto, o comprimento da caixa representa o intervalo interquartil (IQR), outra medida de espalhamento, que neste caso representa 50%. O IQR constitui uma medida mais robusta para o espalhamento do que o desvio padrão ou variância. A barra central mais escura representa a mediana e a linha tracejada em azul a média.

Os valores tracejados acima da caixa representam os extremos superiores da vazão e correspondem a vazões atípicas e os círculos pontos fora da curva. 

Analogamente, os valores tracejados abaixo da caixa representam os valores extremos inferiores de vazão.  No caso de Três Marias, inexistem pontos fora da curva inferiores devido à assimetria da distribuição de probabilidade das vazões.

Observa-se que o comportamento estatístico varia com os meses do ano. Durante o período chuvoso a variação da vazão é maior do que durante o período seco.

Médias, Máximos e Mínimos

A Figura 5 mostra a vazão natural afluente mensal de alguns anos escolhidos especialmente para esta usina. O critério de escolha foi a vazão média anual, e a figura mostra os anos com vazões médias anuais máxima, mínima, média, mediana, as três piores médias anuais históricas até 2019 (2014, 2015 e 2017), e a pior média do período crítico (1955).

A lei de Murphy ⁸ aparece mais uma vez. A vazão média anual mínima encontrada para esta usina ocorreu em 2015, e a média máxima anual aconteceu em 1979, quando Itaipu estava entrando em operação e sobrava energia no país. É importante observar que o valor registrado em 2001, ano do racionamento, representa apenas a 15 menor vazão natural afluente anual da história até agora.

Adicionalmente, o ano do período crítico (1949 a 1956) com menor vazão anual foi 1955, mas ficou muito acima dos outros valores mínimos posteriores.

Apesar desse resultado aparentar um fenômeno produzido pelo aquecimento global, a estatística demonstra que valores extremos de séries temporais estáveis aumentam com o aumento das amostras.

Figura 5. Vazões Críticas de Três Marias (1931 a 2019)

Observa-se claramente a sazonalidade anual e, a partir da comparação com a média de todos os dados (média de longo termo- MLT = 1pu), pode-se determinar o período seco desta usina como o período de abril a novembro. Além disso, a mediana fica claramente menor do que a média durante os meses úmidos e o mínimo dos mínimos mensais é inferior ao pior ano registrado até hoje.

O comportamento sazonal se relaciona com o ciclo anual do sol. Isto pode ser generalizado para todas as usinas hidrelétricas do mundo. Contudo, a amplitude, fase e período dependem da localização geográfica e podem ser consideradas um identificador da bacia hidrográfica. Existem diversas formas de separar o comportamento sazonal da vazão. A primeira consiste em considerar a média anual dos dados mensais. 

A Figura 7 apresenta a média, o máximo, o mínimo, e a média dos valores médios anuais da vazão natural afluente da usina de Três Marias.

Figura 7. Valores médios anuais de vazão natural afluente

Observa-se que a sazonalidade anual, presente na série de médias mensais, desaparece na série de médias anuais. Isto já era esperado porque a função matemática média funciona como um filtro que elimina variações de frequências mais elevadas. Além disso, aparentemente, não existe um comportamento cíclico plurianual bem definido e as variações parecem mais aleatórias.

Isto sugere a hipótese de que as vazões médias anuais podem ser consideradas séries temporais estacionárias de segunda ordem. Esta hipótese permite uma série de simplificações matemáticas nos modelos a serem utilizados, mas requer análise mais detalhada.

Densidade de Probabilidade da Vazão

Mesmo normalizados, os dados apresentados anteriormente não fornecem as informações necessárias para o projeto de usinas hidrelétricas. Por isso, torna-se necessário descobrir o comportamento estatístico da vazão. ⁹

Primeiramente, utilizou-se o histograma, mostrado na Figura 3. 

A definição das classes da variável aleatória, no caso a vazão, requer cuidado. A maneira mais simples consiste em dividir o intervalo da variável aleatória em intervalos iguais. Neste caso, utilizamos 10 intervalos, mas poderíamos ter utilizado 20.

Contudo, utilizar intervalos iguais nem sempre permite visualizar corretamente o comportamento da grandeza aleatória. Por isso, existem outros métodos mais sofisticados que utilizam intervalos variáveis. A Figura 8 apresenta um destes métodos. Este histograma¹⁰ utiliza os mesmos dados da Figura 8, mas com intervalos ajustados pela probabilidade. Desta maneira, foi possível visualizar o comportamento crescente da distribuição de probabilidade para pequenas vazões.

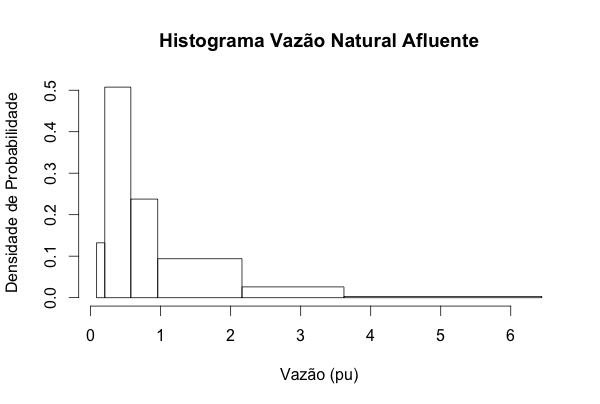
Observa-se um forte crescimento na densidade de probabilidade antes de atingir seu máximo e um lento declínio para vazões superiores. Este comportamento ocorre sempre com grandezas físicas que possuem limitação mínima, mas não possuem restrição física máxima. 

A Figura 10 ¹¹ mostra a distribuição de probabilidade acumulada da vazão natural afluente de Três Marias. Ela fornece a probabilidade de a vazão ser igual ou inferior a um determinado valor. A vazão correspondente a probabilidade de 50% denomina-se mediana e divide o gráfico em duas áreas horizontais iguais. Isto significa que a probabilidade de a vazão ser menor ou maior que a mediana é 50%.

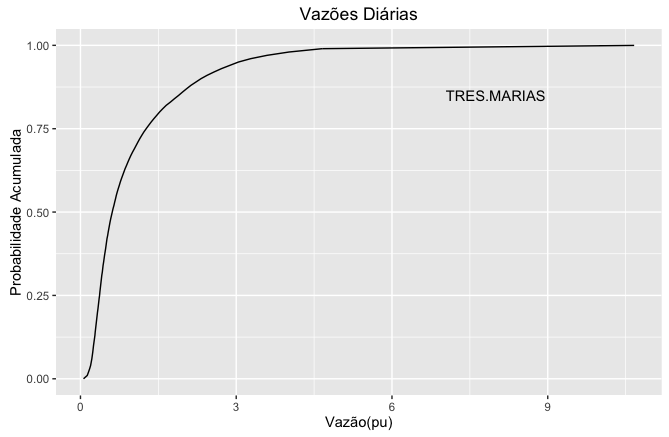
Persistência

A probabilidade acumulada fornece a probabilidade de ocorrência de vazões inferiores (ou superiores) a determinado valor. Contudo, em determinados casos, necessita-se determinar a função inversa, isto é, qual a vazão que ocorre para determinada probabilidade. A Persistência, Figura 11, utiliza o complemento da vazão acumulada ¹² no eixo horizontal e a vazão no eixo vertical. ¹³

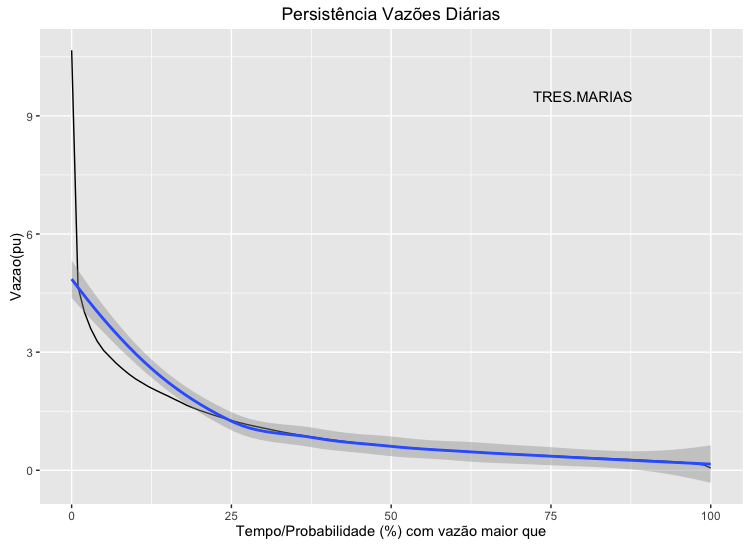
A curva de persistência possui um comportamento não linear, que pode ser melhorado quando utilizamos o logaritmo da vazão para fazer o gráfico, conforme mostra a Figura 12. A persistência do logaritmo da vazão apresenta comportamento aproximadamente linear entre o primeiro quartil (25%) e o terceiro quartil, e esta característica permite a aproximação desta curva por uma reta. ¹⁴

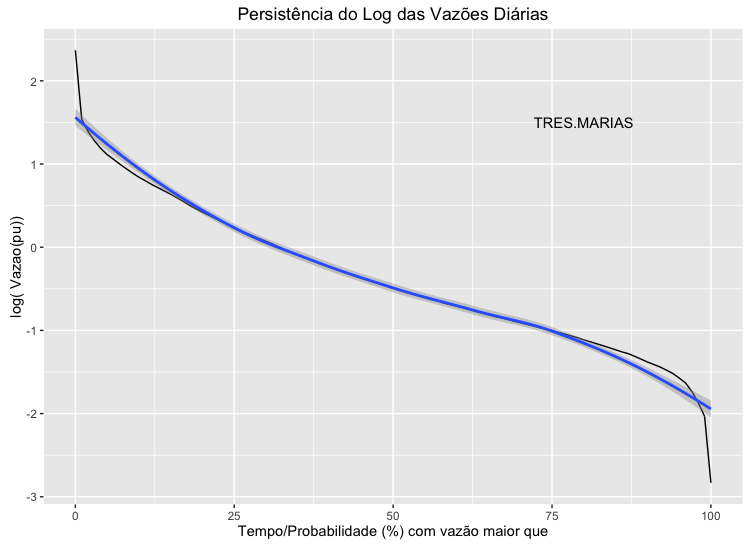
Distribuição de Energia

Conforme visto anteriormente, a potência da geração hidrelétrica depende da vazão e a energia depende do volume. Portanto, a avaliação da distribuição estatística da energia requer a análise do volume. A Figura 13 apresenta o histograma da vazão natural afluente média diária na usina de Três Marias. A diferença entre esta figura e a Figura 3 encontra-se na unidade do eixo vertical. Na figura anterior, utilizamos probabilidade e agora o eixo representa ocorrências.

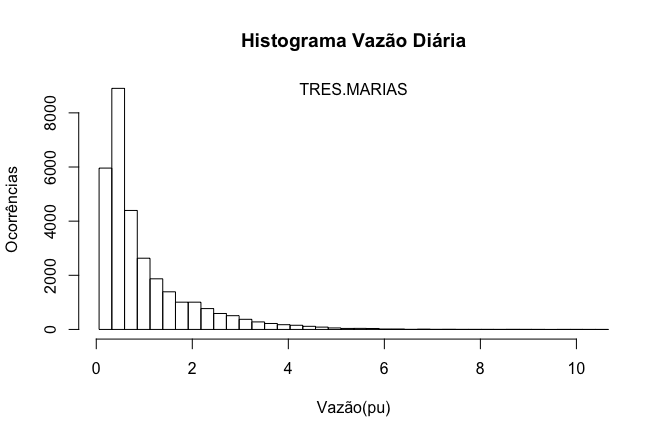
A Figura 14 revela a distribuição estatística da energia, calculada a partir do histograma da vazão natural afluente média diária. Obteve-se os valores deste gráfico a partir da multiplicação das classes de vazão pela probabilidade de ocorrência delas. Como a probabilidade de ocorrência de séries temporais representa tempo, o produto da probabilidade pela vazão normalizada possui dimensão de volume normalizado. Por sua vez, multiplicando o volume em m³ pelo fator de produtibilidade da usina obtemos a energia.

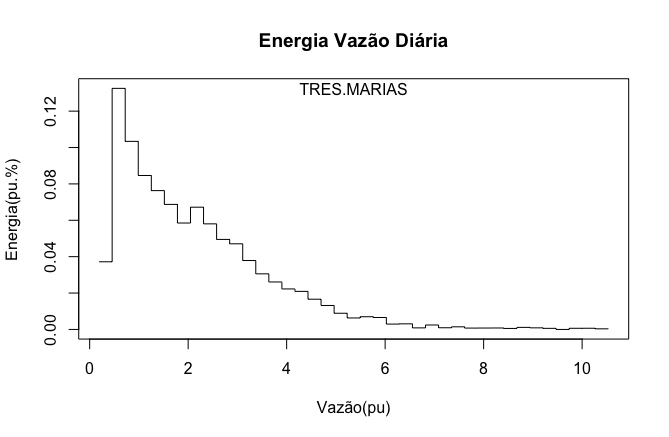
Volume

A determinação do volume de água necessário para regularizar a vazão constitui problema importante no projeto de geração hidrelétrica.

Inicialmente, define-se o volume base anual como sendo o volume de água médio anual que passa por determinada localização. Calcula-se este volume multiplicando a vazão média de longo prazo, em m³/s, pelo número de segundos no ano (31.536.000 s). Isto significa que um metro cúbico por segundo por ano equivale a 0,031536 km³. Mais uma vez, a normalização das grandezas contribui para simplificar a análise dos problemas.

A Equação 1, apresentada anteriormente, fornece a base teórica para o cálculo do volume.

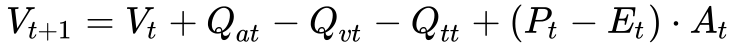
Onde:

• • V_t é o volume do reservatório no instante t;
  • Q_at é a vazão afluente no instante t;
  • Q_vt é a vazão defluente vertida no instante t;
  • Q_tt é a vazão defluente turbinada no instante t.
  • A_t é a área da superfície do reservatório no instante t;
  • P_t é a precipitação no reservatório no instante t;
  • E_t é a evaporação do reservatório no instante t;

Em estudos preliminares de viabilidade, pode-se desprezar a precipitação e a evapotranspiração porque ainda se desconhece a dimensão do reservatório. Além disso, como se desconhece a priori os dados de operação, pode-se considerar o volume de água passando em determinado ponto como sendo o somatório da vazão ao longo de determinado período, conforme a expressão abaixo.

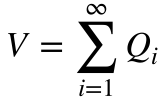
Isto significa que o volume sempre cresce porque as vazões são sempre positivas, o que torna sua análise complexa e inexata. Apesar disso, este método, conhecido como diagrama de Rippl ou de massas, foi desenvolvido no século passado antes do advento das ferramentas computacionais modernas.

Conforme visto anteriormente, se considerarmos a vazão uma série temporal estacionária de segunda ordem, sua média permanecerá constante ao longo do tempo. Isto significa que o crescimento médio do volume também será constante ao longo do tempo. Portanto, podemos retirar o crescimento constante da análise e trabalhar apenas com as variações de volume ao longo do tempo.

Desta maneira, define-se a variação de volume anual se acordo com a Equação 3.

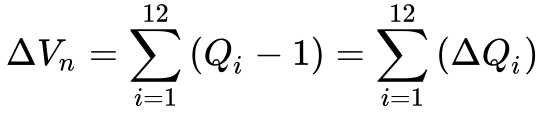
Onde: 

• • ΔV é a variação de volume do ano n normalizado;
  • Qi é a vazão mensal do ano n normalizada;

A Equação 3 mostra que o volume médio anual normalizado possui o mesmo valor numérico que a vazão média anual normalizada, e a diferença se encontra apenas nas bases utilizadas. ¹⁵

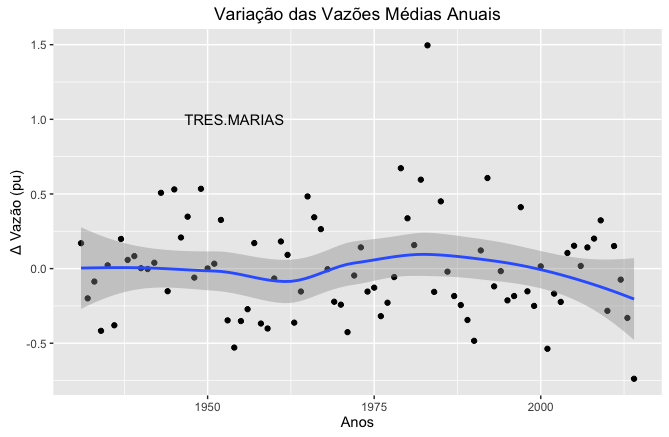
A Figura 15 apresenta a variação da média anual da vazão natural afluente normalizada da usina de Três Marias.

Portanto, este gráfico apresenta as variações anuais de vazão ou volume registradas a cada ano ao redor do valor médio. Observa-se que os valores se distribuem ao redor de zero, com uma pequena oscilação iniciada na década de 50.

A linha azul representa a média móvel das variações, e fornece informações úteis para o dimensionamento do reservatório.

A Figura 16 apresenta a densidade de probabilidade da variação do volume médio anual da usina de Três Marias e mostra que a distribuição de probabilidade se aproxima de uma distribuição normal, apesar de apresentar uma média um pouco inferior a zero e comportamento anormal nos extremos.

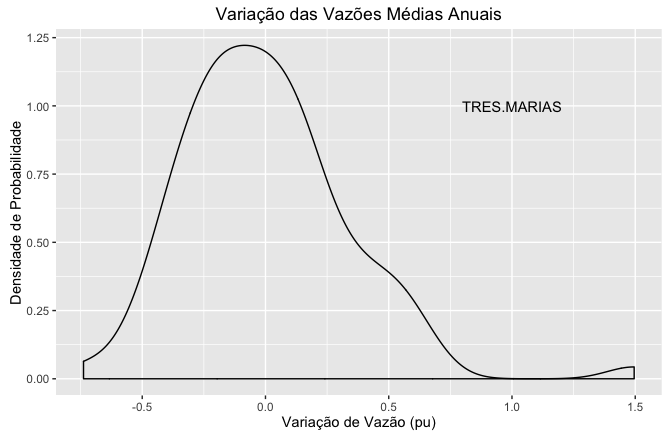
Este comportamento encontra-se de acordo com a Lei dos Grandes Números da Estatística. 

Desta maneira, capturamos apenas variações plurianuais e desprezamos as variações anuais já estudas.

Por definição, considera-se o volume no instante de tempo inicial igual a zero. 

Conforme esperado, os volumes diferenciais anuais oscilam entre valores positivos e negativos uma vez que a média desses valores é zero por definição. Além disso, como seu valor inicial foi considerado igual a zero, seu valor final também será igual a zero.

Com este gráfico podemos determinar os anos de maiores afluências e os de menores afluências.

No caso específico de Três Marias, 1983 foi o ano com maior volume de águas e 2013 o ano com menor volume diferencial anual.

Observamos que enchentes ocorreram periodicamente a cada 13/16 anos e secas ocorreram em maior número, mas com periodicidade aleatória entre 11 e 19 anos.

Por outro lado, observamos que, para este aproveitamento, os anos de 1953 a 1960 e de 1998 a 2003 foram todos abaixo da média. Isto ajuda a explicar um pouco o racionamento de 2001.

Referências

1. Rozenholc, Y, Mildenberger, T. and Gather, U. , Combining regular and irregular histograms by penalized likelihood. Discussion Paper 31/2009, SFB 823, TU Dortmund.
2. Wiilks, Daniel. Statistical Methods in the Atmospheric Sciences. San Diego: Elsevier Science Co, 2011. Print.