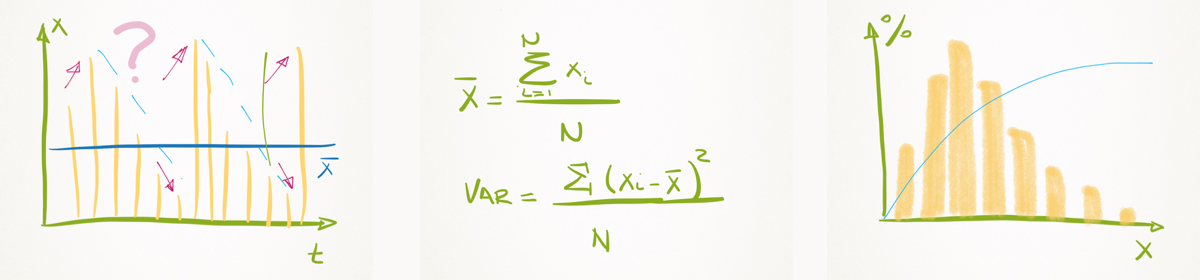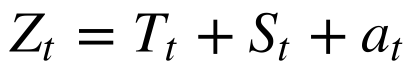Estatística

“A Estatística é a única ciência que permite dois especialistas tirarem conclusões diferentes a partir dos mesmos dados”

Evan Esar, humorista americano

A Estatística possui papel de destaque na geração de energia elétrica porque fornece as melhores ferramentas para extrair informação de grandes volumes de dados.

A demanda de energia, a água nas hidrelétricas, o sol na geração solar, os ventos na geração eólica e o preço dos combustíveis apresentam comportamentos randômicos e a estatística, deixando o humor de lado, permanece como a melhor ferramenta para estudá-los.

Espaço de Amostragem

Espaço de amostragem – S – ou População consiste no conjunto de todos os possíveis valores das grandezas aleatórias estudadas. Mais precisamente, o conjunto de todos os possíveis eventos simples ou elementares constitui o espaço de amostragem. Por exemplo, o conjunto de todas as possíveis vazões de determinado ponto de um rio representa um espaço de amostragem. Isto nos leva às seguintes questões práticas:

• • É possível quantificar o espaço de amostragem?
  • É possível determinar seus valores máximo e mínimo?
  • É possível prever seu comportamento?

Os espaços de amostragem podem ser finitos ou infinitos dependendo da grandeza estudada. Espaços Finitos possuem uma quantidade finita de elementos, e Espaços Infinitos possuem uma quantidade infinita de elementos. Por exemplo, a vazão de um rio possui Espaço Infinito porque pode variar continuamente entre zero e infinito, mas o número de turbinas em operação possui Espaço Finito porque varia discretamente entre zero e o número de máquinas instaladas.

Evento

Evento representa um subconjunto A do espaço de amostragem S. Eventos podem ser Simples ou Compostos. Denomina-se Evento Elementar ou Simples um subconjunto unitário do Espaço de Amostragem. Por outro lado, conjuntos formados por diversos elementos simples formam os Eventos Compostos. Por exemplo, cada velocidade de vento medida representa um Evento Simples, e o conjunto de vazões semanais de um rio constitui um Evento Composto.

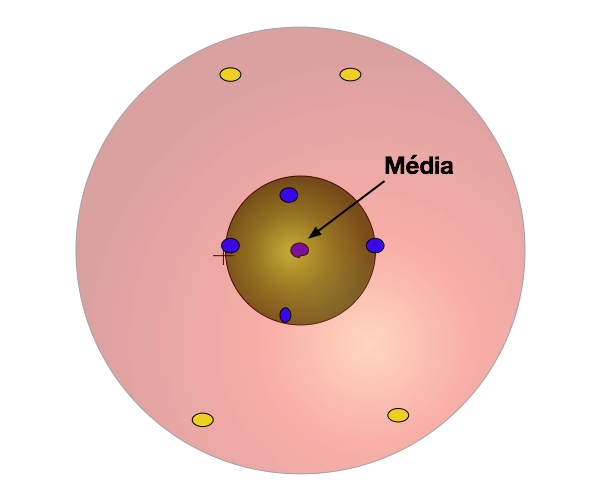
Considere os pontos coloridos na Figura 1 como Eventos Simples de um mesmo espaço de amostragem (o alvo). A necessidade de medir a localização e o espalhamento destes eventos surge naturalmente. Intuitivamente, apesar de nenhum dos eventos ter acertado o centro do alvo, o centro representa a medida de localização de todos os eventos. Por outro lado, a distância dos pontos ao centro mede o espalhamento dos eventos. Outros parâmetros poderiam ser criados para medir a localização e o espalhamento.

Probabilidade

No caso de Espaços de Amostragem Finitos, define-se a probabilidade P(A) como h/n, onde h é o número de ocorrências do evento A e n o número de Eventos Simples do Espaço Amostral. Por exemplo, a probabilidade de um determinado número sorteado na Megasena é igual a 1/60.

No entanto, qual a probabilidade de a vazão de uma usina hidrelétrica ser inferior à mínima registrada nos últimos 80 anos? Para responder a esta pergunta necessitamos definir probabilidade em Espaços de Amostragem Infinitos. Neste caso, define-se probabilidade da seguinte maneira:

De acordo com Spiegel, “Se após n repetições de um experimento, sendo n um número suficientemente grande, um determinado Evento A ocorreu h vezes, define-se a probabilidade do Evento A da seguinte maneira: P(A)=h/n.”[1]

O problema desta definição reside em determinar o conceito de “grande o suficiente” para garantir a convergência da probabilidade e, dado um n finito, qual o erro cometido. Na prática, quanto maior o número de dados medidos menor será o erro.

Axiomas

• • A probabilidade é sempre positiva.
  • A probabilidade é sempre menor ou igual a 1.
  • A probabilidade de um evento é 1 quando o evento sempre ocorre.
  • A probabilidade de um evento é zero quando jamais ocorre.
  • Se o Evento A’ é o complemento de A, então P(A’) = 1-P(A)
  • Somatório ou integral das probabilidades de todos os Eventos Simples de um espaço S é sempre igual a 1.
  • Para quaisquer dois eventos A e B, a probabilidade da união dos dois eventos corresponde a soma das probabilidades dos eventos menos a probabilidade de os eventos ocorrerem simultaneamente. Se eles forem mutuamente excludentes, a probabilidade da união é a soma das probabilidades individuais.

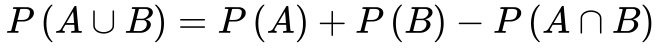
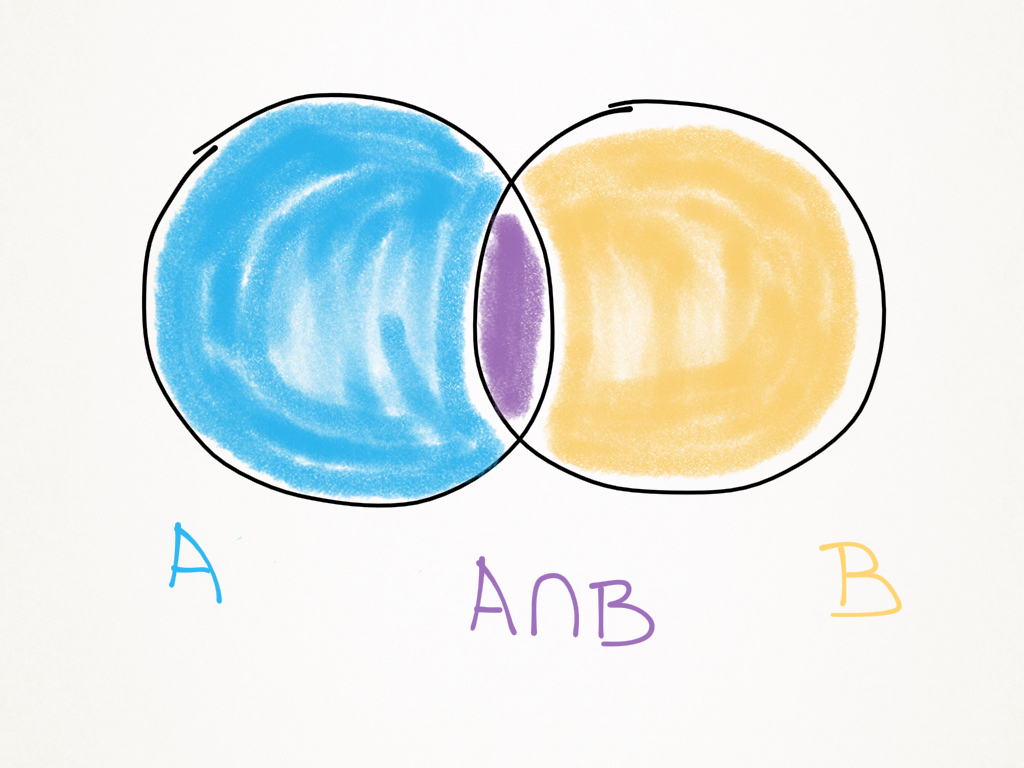
Probabilidade Condicional

Sejam A e B dois eventos de um espaço S com probabilidades maiores que zero. A Equação 2 determina a probabilidade de A ocorrer dado que B também ocorre.

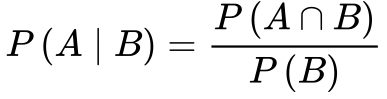
Distribuição de Probabilidade

Se associarmos um número x a cada ponto de um espaço de amostragem a Função Probabilidade ou Distribuição de Probabilidade – f(x) será igual a probabilidade de x. Se o espaço de amostragem for finito as variáveis randômicas ou estocásticas serão discretas. Caso contrário, as variáveis são contínuas.

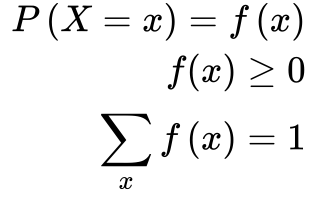
Distribuição Acumulada

A Função de Distribuição Acumulada é a soma ou a integral da distribuição de probabilidade entre 0 e o ponto x.

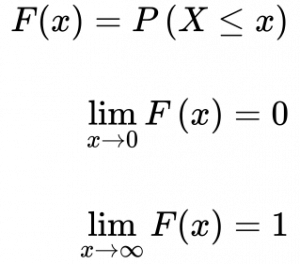
Valor Esperado e Média

O Valor Esperado – E(x) – de uma variável aleatória x constitui um dos conceitos mais importantes da estatística. Ele representa o valor esperado ou mais provável de uma variável aleatória. Calcula-se o valor esperado de determinada variável aleatória x de acordo com a equação 5.

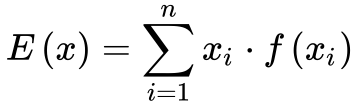
No caso particular de as probabilidades serem iguais, o valor esperado equivale à média aritmética. ¹

A rigor, o valor esperado se encontra associado a eventos ou amostras de determinado espaço amostral enquanto a média estatística – μ – representa os dados de toda a população ou quando a função de distribuição de probabilidade é conhecida. Porém, na prática esta distinção nem sempre se encontra bem definida e utilizam-se os termos valor esperado e média algumas vezes de forma incorreta.

Deve-se ressaltar que a média estatística só se iguala à média aritmética quando todos os eventos possuem a mesma probabilidade de ocorrer. A média estatística consiste no conceito estatístico mais utilizado na prática e pertence ao grupo de medidas de localização.

Teoremas Sobre Valor Esperado

• • O valor esperado é uma função linear.

• • O valor esperado de amostras de uma população é a média da população.

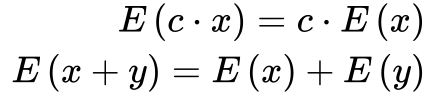
Moda

A Moda de uma variável randômica representa o valor que ocorre com maior frequência ou com maior probabilidade. Quando isto ocorre, a derivada da função probabilidade é igual a zero. Existem variáveis randômicas com mais de uma moda. Neste caso, denominam-se de bimodal ou multimodal. A Moda também representa uma variável de localização.

Mediana

A mediana é o valor da variável randômica que separa a função de distribuição acumulada em duas metades, possui o valor de probabilidade de 50% e equivale ao percentil de 50%. A mediana e média nem sempre se igualam. A mediana, média, e moda se igualam apenas em distribuições de probabilidade simétricas, como no caso da distribuição normal ou gaussiana.

A mediana é a medida mais robusta e resistente da tendência central de uma variável aleatória e servindo também como medida de localização.

Medidas robustas não fornecem a solução ótima para problemas específicos, mas produzem resultados satisfatórios para a maioria dos problemas. Medidas robustas são normalmente insensíveis a pressupostos sobre as características das variáveis. Por exemplo, a média é a melhor medida do centro de uma variável aleatória se ela tiver um comportamento simétrico. Por isso, a média não é uma medida robusta. Por outro lado, medidas resistentes são insensíveis a “pontos fora da curva” ou grandes variações de poucos pontos. A média também é mais sensível do que a mediana a valores fora da curva. 

Momento de Ordem r

Apenas o valor esperado não caracteriza uma variável aleatória. Duas variáveis podem ter a mesma média, mas ter distribuições de probabilidade diferentes, conforme mostra a Figura 3. A média das duas variáveis é zero, mas a variável #2 está menos concentrada do que a variável #1.

Figura 3. Distribuição de Probabilidade de dados com a mesma média

Portanto, a caracterização de variáveis aleatórias requer outros parâmetros.

Define-se o Momento de ordem r de uma variável aleatória X como:

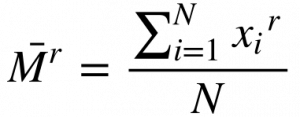
Onde:

• M^r é o momento de ordem r;
• r é a ordem;
• x_i é a variável aleatória;
• N é o número de variáveis na amostra.

Observa-se que o momento de ordem 1 representa a média aritmética da variável aleatória.

Define-se o momento de ordem r ao redor da média da seguinte maneira:

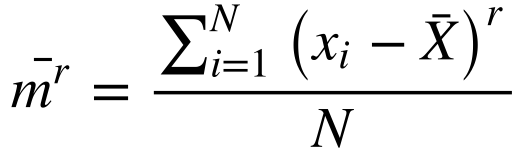
O momento ao redor da média de ordem 1 é zero. 

Variância e Desvio Padrão

O momento de segunda ordem centrado na média – μ₂– consiste no primeiro momento diferente de zero e se tornou conhecido como variância. Como a variância possui dimensão igual ao quadrado da dimensão da variável aleatória, perde-se o sentimento da unidade deste número. Para fugir deste inconveniente, define-se o desvio padrão – σ – como a raiz quadrada da variância. Desta forma, o desvio padrão possui a mesma dimensão da variável aleatória em questão.

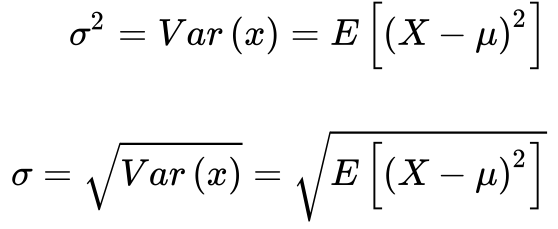
Covariância

Define-se a covariância – σ_xy – entre duas variáveis aleatórias X e Y como o valor esperado entre os erros das duas variáveis.

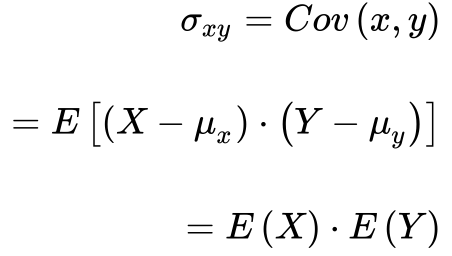
A covariância possui a dimensão do produto das dimensões das variáveis aleatórias.

Correlação

Para fugir do problema da dimensão da covariância, define-se a correlação – ρ – entre duas variáveis aleatórias X e Y como sendo a covariância normalizada pelo produto dos desvios das variáveis. Deve-se tomar cuidado com a interpretação da correlação porque ela mede a correlação linear entre as variáveis, mas não identifica correlações não lineares. ²

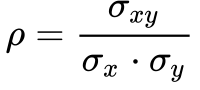
Teoremas Sobre Variância

Como a Variância não é uma função linear, torna-se importante analisar algumas de suas propriedades. A Variância do produto de uma variável estocástica X por uma constante c resulta em:

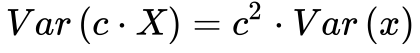
Além disso, a Equação 13 fornece o valor da variância da soma/subtração de duas variáveis aleatórias.

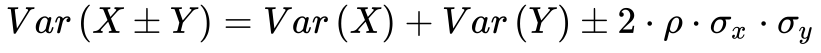
Por exemplo, Equação 14 apresenta a soma das potências de duas hidrelétricas quaisquer.

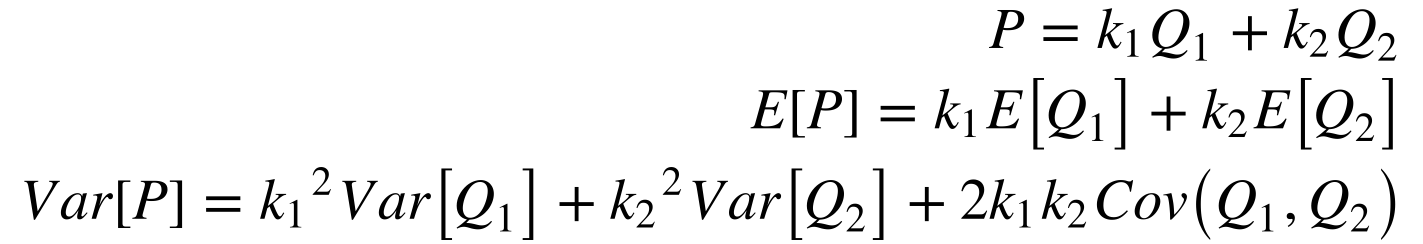
Isto significa que o valor esperado da potência aumenta, mas sua variância pode aumentar ou diminuir em função da correlação entre as vazões. Por isso, o ideal seriam usinas com correlações negativas para minimizar o risco de faltar energia.

Distorção (Skewness)

Conforme vimos anteriormente, a média, moda e mediana nem sempre se igualam. Na verdade, a simetria da distribuição de probabilidade em relação à média consiste em condição necessária para que elas sejam iguais.

A distorção mede o grau de assimetria da distribuição de probabilidade de uma variável aleatória em relação ao valor esperado. Define-se a distorção como sendo o momento ao redor da média de terceira ordem dividido pelo desvio padrão ao cubo.

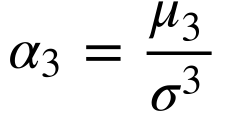
A distorção pode ser positiva ou negativa conforme a distorção seja para a direita ou esquerda respectivamente. Distorção igual a zero significa uma distribuição perfeitamente simétrica em relação ao valor esperado, como a distribuição normal.

Curtose (Kurtosis)

A curtose mede a probabilidade dos valores extremos da distribuição de probabilidade ou a probabilidade da moda. Define-se a curtose como o momento de quarta ordem ao redor da média dividido pelo desvio padrão elevado a quatro.

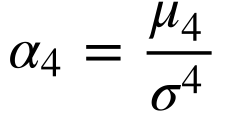
Utiliza-se a distribuição de probabilidade normal, que possui curtose de 3 como referência.

Valores menores do que 3 representam distribuições com extremos reduzidos e valores maiores do que 3 representam distribuições com extremos mais prováveis.

Boxplot

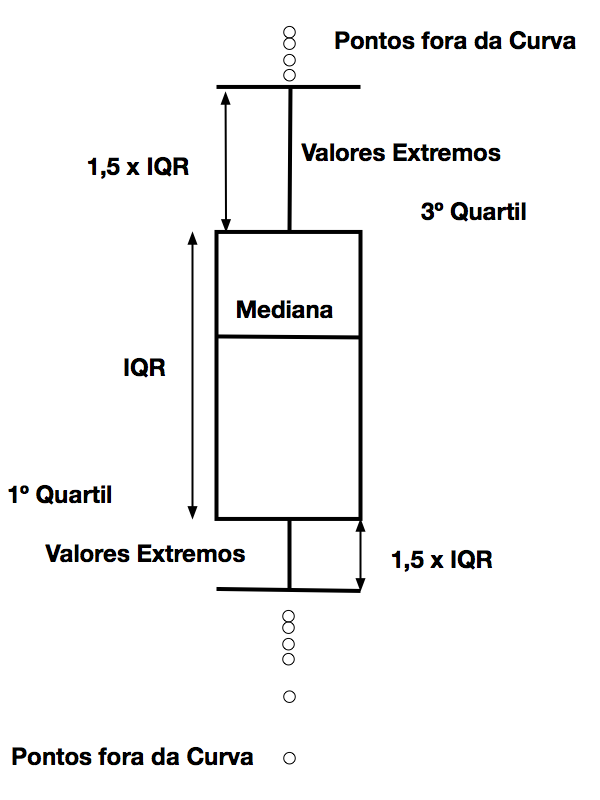
Como a estatística trabalha com grandes quantidades de dados, surge a necessidade de apresentar informações de forma simples e direta. O gráfico Boxplot permite apresentar um conjunto importante de grandezas estatísticas de forma clara e simples.

O retângulo delimita 50% de probabilidade de ocorrência da variável e se encontra delimitado pelo primeiro quartil ³ e o terceiro quartil ⁴. A mediana⁵, que representa 50% de probabilidade de ocorrência, divide esse retângulo em duas partes nem sempre iguais.

Os valores extremos surgem abaixo do Primeiro Quartil e acima do Terceiro Quartil até valores 1,5 vezes o IQR – Interquantile Range, que podemos traduzir como Amplitude Interquartil. O valor do fator multiplicativo de 1,5 é arbitrário ⁶, pode ser ajustado conforme a aplicação específica.

Propositalmente, a Figura 4 mostra que o fator multiplicativo somente deve ser igual para os pontos superiores e inferiores quando a distribuição estatística dos dados for simétrica.

Lei dos Grandes Números

O valor esperado da soma de variáveis aleatórias mutuamente independentes, cada uma com sua média e variância, tende para a média aritmética das médias das variáveis quando o número de variáveis tende a infinito. Além disso, a distribuição de probabilidade da soma de variáveis randômicas tende para uma distribuição normal.

Percentis

A função probabilidade acumulada fornece a probabilidade P para valores menores que X. A função percentil representa a função inversa da função probabilidade acumulada. Dado um valor de probabilidade, ela fornece o valor de X. A figura abaixo mostra a probabilidade acumulada de duas variáveis aleatórias. Neste caso, o percentil de 50% (mediana) é o mesmo para as duas variáveis e vale zero. Contudo, os percentis de 25% e 75% são diferentes, eles medem a variação da variável aleatória ao redor da variável de localização.

Figura 5. Probabilidade acumulada 

Séries Temporais

Denomina-se de Séries Temporais as funções aleatórias de uma variável independente relacionada com o tempo.

A impossibilidade de prever o comportamento futuro caracteriza as séries temporais porque não existe uma função ‘determinística’ do tempo que represente a série.

Fórmulas matemáticas podem prever as órbitas de planetas e satélites com precisão porque as equações da física representam o sistema.

Por outro lado, fenômenos naturais, tais como vazão, precipitação, velocidade do vento, direção do vento e irradiação solar, não podem ser descritos por funções matemáticas de forma determinística.

Porém, podemos descrever estes fenômenos como um Processo Estocástico.

Processo Estocástico

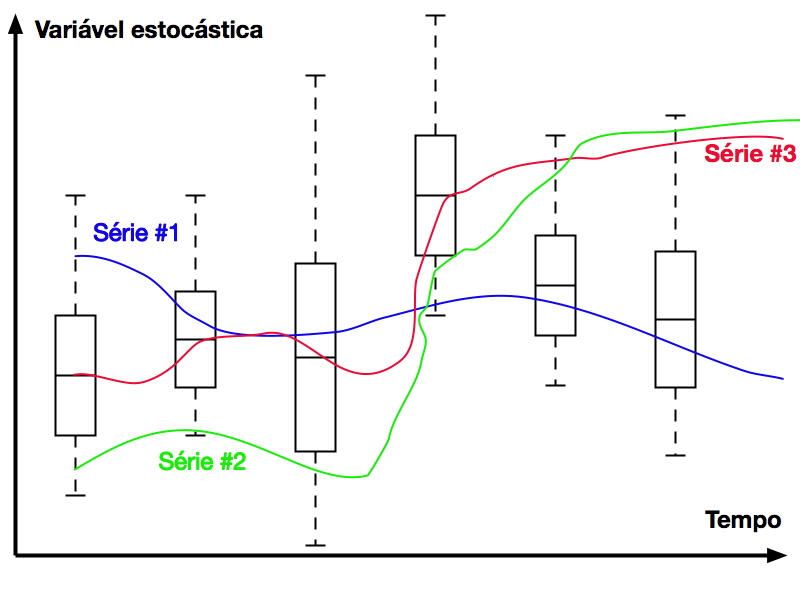
Define-se Processo Estocástico como uma família de funções aleatórias Z(t,w). A variável t pertence ao conjunto T e a variável w pertence ao conjunto W. A função Z representa um conjunto de distribuições de probabilidade que variam com o tempo.

Séries Temporais constituem uma amostragem do conjunto Z(t,w) e podemos interpretá-las como possíveis trajetórias do processo estocástico no tempo.

Os Processos Estocásticos podem ser classificados em:

• • Estacionários;
  • Normais ou Gaussianos;
  • Markovianos.

Define-se Processo Estocástico Estacionário como o processo estocástico que independe da origem dos tempos. Neste caso, as funções Z(w) são iguais ao longo do tempo. Isto significa que o processo se encontra em equilíbrio estatístico. Este conceito é matematicamente forte, mas de difícil aplicação.

Processo Estocástico Estritamente Estacionário representa aquele onde todos os momentos estatísticos das funções Z(w) dependem apenas das diferenças t_j-t_i, assim como os momentos de todas as distribuições bidimensionais [Z_tn, Z_tm]. Este conceito não é tão forte quanto ao anterior, mas contínua de difícil aplicação.

Finalmente, Processo Estocástico Fracamente Estacionário ou Estacionário de Segunda Ordem é aquele onde:

• • O valor esperado das funções aleatórias Z são iguais e constantes ao longo do tempo;
  • O valor esperado da variância de todas as funções aleatórias Z são finitos;
  • A covariância entre todos e quaisquer pares de funções aleatórias Z_i e Z_j depende apenas do módulo de t_i-t_j.

Processo Estocástico Gaussiano é aquele onde todas as funções aleatórias Z apresentam distribuição normal ou gaussiana.

Processos Estocásticos Markovianos são os processos estocásticos sem memória.  Isto é, os estados futuros do processo dependem apenas do estado atual do processo. 

Análise de Séries Temporais

Existem dois tipos de modelos de análise de séries temporais; os paramétricos e os não-paramétricos. Modelos paramétricos possuem número finitos de parâmetros e os não-paramétricos possuem infinitos parâmetros.

Exemplos de modelos paramétricos são:

• • modelos de erro ou de regressão;
  • modelos de autorregressão e média móvel – ARMA;
  • modelos de autorregressão integrada e médias móveis – ARIMA;
  • modelos de memória longa – ARFIMA;

Exemplos de modelos não paramétricos são:

• modelos de autocorrelação e espectrais; transformada de Fourier e Wavelets.

Toda série temporal pode ser decomposta numa sequência determinística e outra aleatória do tempo.

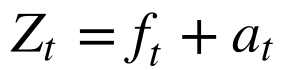
Onde:

• • Z_t é a série temporal;
  • f_t é a parte determinística ou sinal;
  • a_t é a parte aleatória ou ruído;

Dependendo do comportamento e características das funções f e a, algumas simplificações são possíveis e os diversos modelos foram desenvolvidos.

Modelos de Erro ou Regressão

Os modelos mais simples, chamados de erro ou regressão, ocorrem quando a parte determinística da série temporal independe da parte aleatória e a parte aleatória independe do tempo.

Matematicamente, isto significa que:

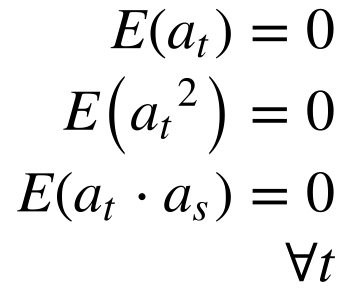
Onde:

• • E é o valor esperado.

Dependendo do tipo de função f_t , classifica-se o modelo em:

• • Modelo de Tendência Linear;
  • Modelo de Regressão;
  • Modelo Oscilatório.

Modelo de Tendência Linear

No modelo de tendência linear, a parte determinística da série temporal depende apenas de dois parâmetros constantes; α e β.

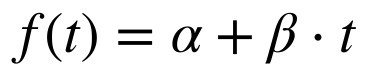
Modelo de Regressão

No modelo de regressão, uma função linear de uma variável observável dependente do tempo determina a parcela determinística da função.

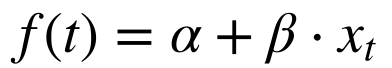
Modelo Oscilatório

Modelos oscilatórios utilizam a série de Fourier, a Transformada de Fourier, a Transformada Rápida de Fourier e Wavelets. Independentemente da técnica utilizada, o objetivo deste modelo consiste em identificar os modos de oscilação existentes no processo analisado. 

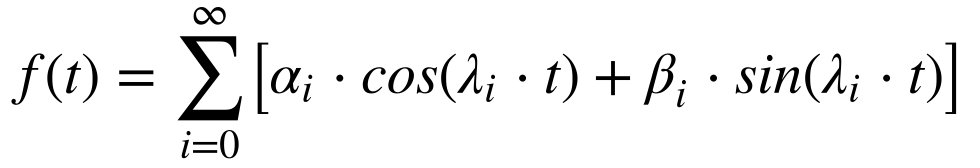
Modelos de Auto-Regressão

Admitir a inexistência de correlação entre a vazão⁷ de hoje com a vazão de ontem não se sustenta na prática. O senso comum nos diz que uma boa estimativa do tempo de amanhã baseia-se na observação do tempo hoje.

Porém, a característica dos processos estocásticos consiste em variar de forma aleatória essa correlação.

Os modelos de auto-regressão permitem representar sistemas físicos com correlação temporal. Existem basicamente três classes de modelos de auto-regressão:

• • Processos Lineares Estacionários;
  • Processos Lineares não Estacionários Homogêneos;
  • Processos de Memória Longa.

Tendência e Sazonalidade

Tradicionalmente, os estudiosos decompões as séries temporais em duas parcelas determinísticas: Tendência e Sazonalidade.

Onde:

• • T_t é a tendência;
  • S_t é a sazonalidade;
  • a_t é a parcela aleatória, que possui média zero e variância σ²_t.

A parcela a_t possui média zero porque a média ficou incluída na tendência.

Tendência

A tendência pode ser obtida pelos métodos de erro ou regressão apresentados acima. Em particular, utiliza-se a aproximação polinomial. Na prática, a aplicação deste método nos dados brutos pode levar a polinômios de ordem muito elevada, que acabam complicando o problema. A maneira elegante de resolver esta questão consiste na aplicação da aproximação polinomial nos dados brutos filtrados.

Referências

1. BARTHOLOMEW, D.J., What is Statistics?, J.R. Statist. Soc. A (1995) 158, Part1, pg. 1-20.
2. BOX,G.E.P., JENKINS, G.M., REINSEL, G.C., Time Series Analysis – Forecasting and Control, 4 edição, John Wilwy & Sons, 2008.
3. COWPERTWAIT, P.S.P., METCALFE, A.V., Introductory Time Series with R, Springer, 2009.
4. CRYER, J.D., CHN, K.S., Time Series Analysis with Applications in R, 2 edição, Springer, 2008.
5. HSU, H., Probability, Random Variables & Random Processes, McGraw-Hill, 1997.
6. MORETTIN,P.A., TOLOI, C.M.C., Análise de Séries Temporais, Edgard Blücher, São Paulo, 2004.
7. SPIEGEL, M.R., SCHILLER, J., SRINIVASAN, R.A., Probability and Statistics, 2 edição, Coleção Schaum, McGraw-Hill, 2000.
8. WEI, W.S.W., Time Series Analysis – Univariate and Multivariate Methods, 2 edição, Pearson, 2006.
9. WILKS, D. S., Statistical Methods in the Atmospheric Sciences, 3 edição, Elsevier, 2011.