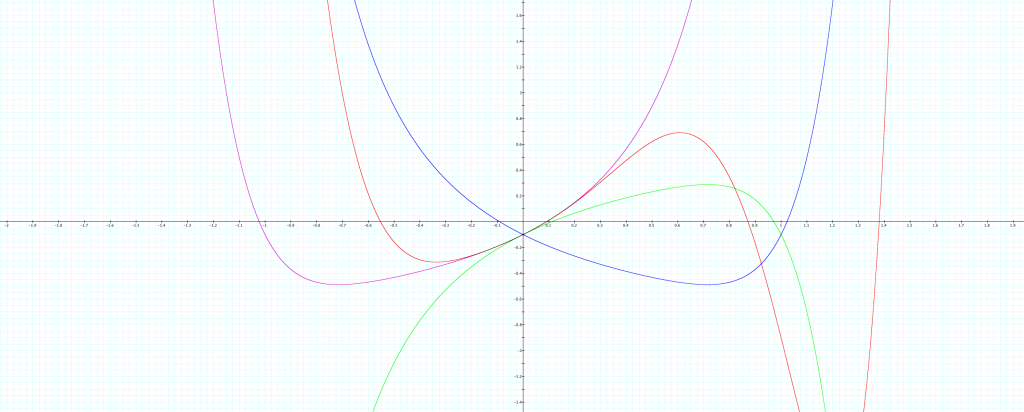
Resolver equações não lineares faz parte de importantes problemas práticos da engenharia. Existem diversas metodologias para resolver este problema, mas a comunidade científica consagrou o método de Newton-Raphson.
Equações não-lineares não possuem soluções analíticas, e os método numéricos continuam a única forma de resolvê-las.
De acordo com o método de Newton-Raphson, dada uma função qualquer f(i), que possua derivada f'(i), o valor de i que resolve a equação f(i)=0 será dado por:
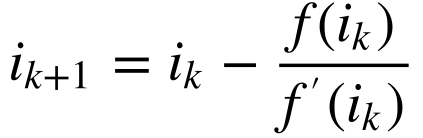
Onde:
- k é o número da iteração;
- f é a função;
- f’ é a derivada da função;
- i é a variável que desejamos encontrar;
- k é o número da iteração.
Este método necessita de um valor inicial para iniciar o processo de busca da solução. Dependendo da função e desse valor inicial, o processo pode divergir e não encontrar a solução correta.
Exemplo #1
Determine a taxa de desconto (i) de uma série de n pagamentos (Pmt) iguais e valor presente Vp.
As funções f(i) e f'(i) abaixo resolvem este problema.
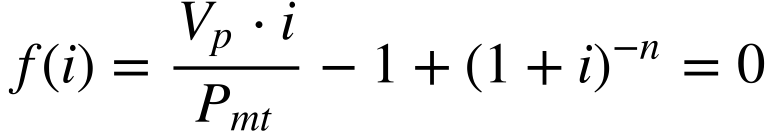
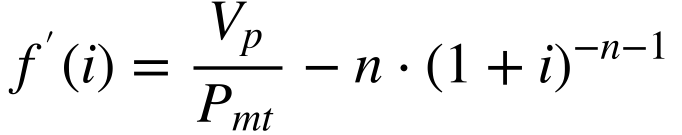
Onde:
- Vp é o valor presente;
- Pmt é o valor do pagamento periódico;
- i é a taxa de desconto;
- n é o número de pagamentos periódicos.
Considerando o chute inicial igual a 5%, a tabela e a figura abaixas mostram que o método convergiu em 3 iterações.
n=20, Vp/Pmt=10, i(0)=5%
k i(k) [%] f(ik) f'(ik)
0 5,0 -0,12 2,82
1 9,4 0,10 6,95
2 7,9 0,01 5,93
3 7,8 0,00 5,83
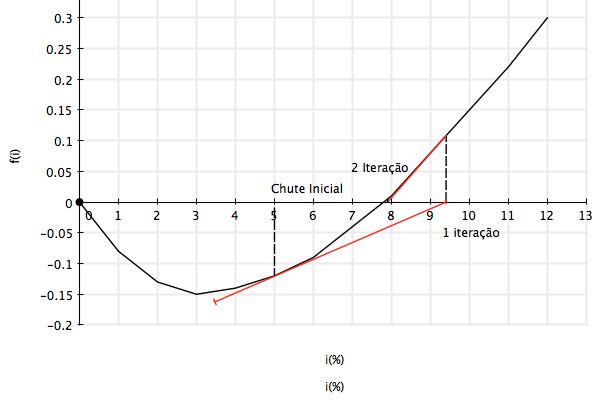O que aconteceria se o chute inicial tivesse sido menor do que 3?
O que aconteceria se o chute inicial fosse zero?
Exemplo #2
Determine a taxa interna de retorno de um fluxo de caixa genérico.
A determinação da taxa interna de retorno (TIR) requer a solução da equação abaixo.
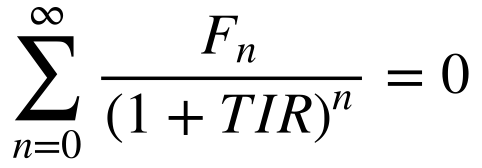
A substituição de variável abaixo facilita a solução do problema.
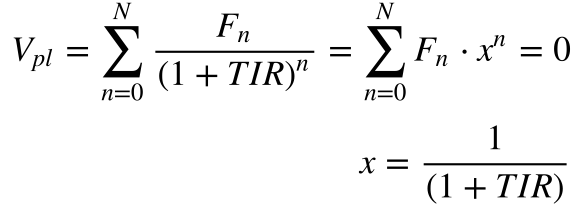
Desta forma, o problema de encontrar a TIR transformou-se na determinação das raízes (os valores de x) de um polinômio de grau N com coeficientes reais.
Isto significa que existem N possíveis soluções; reais ou complexas. Soluções complexas não possuem significado financeiro e, consequentemente, são desconsideradas. 1
Matematicamente, a taxa interna de retorno pode assumir valores positivos ou negativos. Apesar de possíveis, taxas negativas são indesejáveis porque representam prejuízo.2Portanto, consideramos apenas taxas de retorno positivas porque simplifica a solução do problema, em decorrência da variável auxiliar x ser sempre menor do que um neste caso. Consequentemente, os termos da série da equação 5 convergem rapidamente para zero, e podemos aplicar teoremas matemáticos importantes.
Segundo Descartes, o número de raízes reais e positivas de qualquer polinômio depende do número de variações de sinal dos seus coeficientes. 3 Neste caso, o número de taxas de desconto positivas possíveis depende do número de variações de sinal das receitas líquidas. De acordo com esta regra, o número de soluções possíveis maiores que zero será menor ou igual que o número de variações de sinal.
Além disso, a diferença entre o número de variações de sinal e o número de raízes reais positivas é sempre um número par e inteiro. Por exemplo, fluxos de caixa com valor inicial negativo (investimento) seguidos de receitas líquidas positivas apresentam apenas uma ou nenhuma TIR positiva. Contudo, como a diferença entre o número de variações e o número de soluções positivas deve ser par, fluxos de caixa com apenas uma variação de sinal possuem necessariamente uma TIR positiva. Esta conclusão independe da ordem do polinômio, neste caso, do número de períodos do fluxo de caixa.
Taxas de desconto negativas são possíveis, apesar de indesejáveis. O número de raízes reais negativas de determinado polinômio depende do número de variações de sinal dos coeficientes de p(-x). A alteração do sinal de x acarreta mudança de sinal apenas dos coeficientes de exponentes ímpares, e obtém-se o número de raízes negativas aplicando as regras anteriores.
As equações abaixo fornecem as funções para o método de Newton-Raphson referentes à equação 5, e são polinômios da variável x.
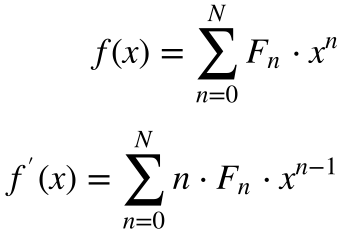
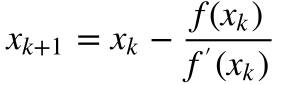Equação 6Determina-se o valor da TIR a partir da equação 5 após se encontrar o valor de x.
O objetivo da equação consiste em determinar precisamente o valor de x para f(x)=0, e a derivada da função existe apenas para acelerar o processo. Por isso, pode-se aproximar o valor da derivada pelos seus fatores iniciais.
A Tabela abaixo apresenta quatro fluxos de caixa com quantidades distintas de trocas de sinal. Observa-se que, dependendo do número de inversões de sinal no fluxo de caixa, o número de soluções reais positivas varia.
Fluxos de Caixa
n Fluxo #A Fluxo #B Fluxo #C Fluxo #D
0 -0,1 -0,1 -0,1 -0,1
1 1 -1 1 1
2 1 1 1 -1
3 1 -1 1 1
4 1 1 1 -1
5 1 -1 -0,1 1
6 1 1 1 -1
7 1 -1 1 1
8 1 1 1 -1
Referências
HAUSER, J.R., Numerical Methods for Nonlinear Engineering Models, Springer, 2009.