A Figura 1 apresenta cristais com formas geométricas diferentes das sete apresentadas anteriormente, e algumas dessas formas encontram-se na Figura 2. O corte ou crescimento dos cristais em determinados planos explicam estas novas formas. Mas como definir precisamente a enorme quantidade de planos possíveis?
Em 1839, o mineralogista Wiliam Miller criou um sistema para designar de forma precisa todos os planos.

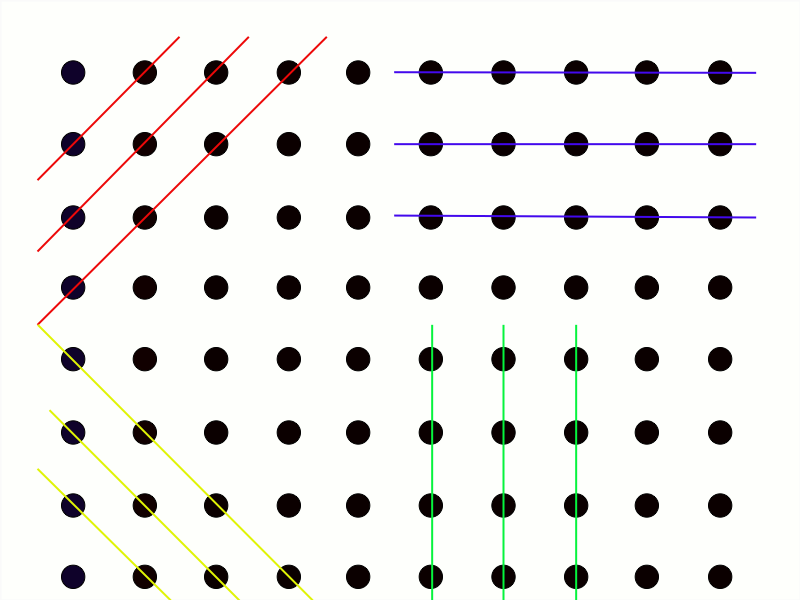
Os Planos Cristalinos são planos paralelos, periódicos, e fictícios que unem pontos da Rede Cristalina, conforme mostra a Figura 3.
Como teoricamente as redes cristalinas são infinitas, existem infinitos planos, mas observa-se que existem finitas famílias de planos.1
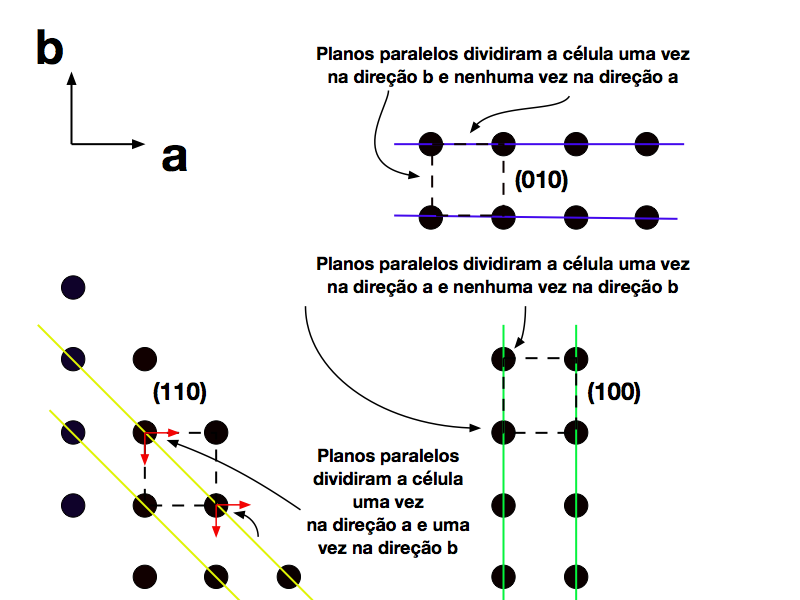
Os Índices de Miller, formados por conjuntos de três números inteiros (h,k,l), foram criados para designar de forma universal as famílias de planos. Estes números representam em quantas vezes o plano divide os lados da célula unitária nas direções a,b,c.
A Figuras 3 permite visualizar melhor este conceito. Nela aparecem os três casos simples e básicos, onde a distância entre planos coincide com o tamanho da célula e o eixo c encontra-se perpendicular ao plano da figura e, por isso, não aparece. Observa-se que h torna-se 1 quando o plano é perpendicular à direção a e zero quando paralelo. Isto contraria um pouco a noção vetorial, mas todo o mundo da Cristalografia o adota.
No caso de planos paralelos inclinados com relação à célula unitária, passam a existir valores para h e k[efn-note] e l se o eixo c estiver presente.[/efn_note]
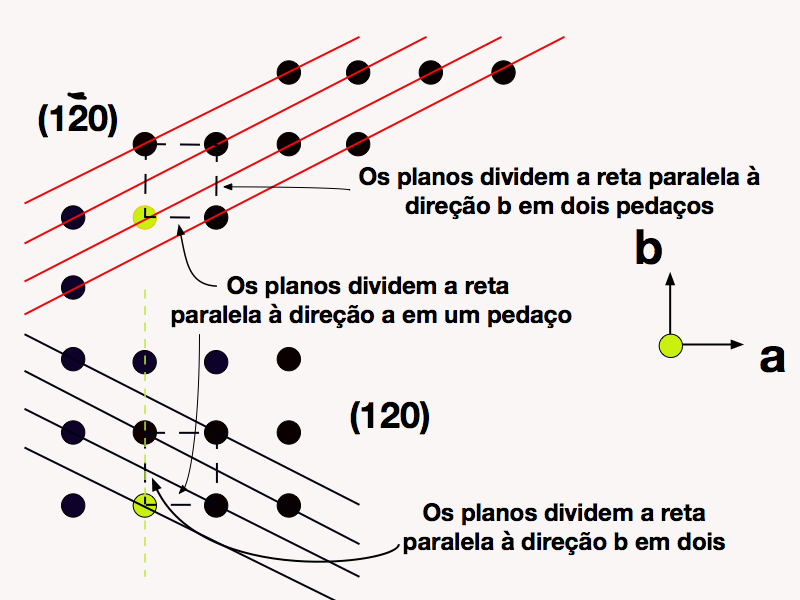
A Figura 4 mostra exemplos com distâncias entre os planos menores, que possuem duas possibilidades de orientação relativa. Em ambos os casos, os planos dividem o eixo b em duas partes e o eixo a em uma, logo a notação de ambos deveria ser (120). Porém, os planos são claramente distintos e devem possuir representações diferentes, um deles deverá ter uma coordenada negativa2 e o outro positiva.
Para solucionar esta questão, adotou-se a convenção de considerar o ponto verde na figura como referência. A escolha deste ponto resulta em coordenadas positivas para todos os outros pontos da célula. Para determinar o sinal do índice k, considere um outro plano que corte o eixo a da célula de referência escolhida, se este plano cortar o eixo b na parte positiva, o índice k será positivo. No caso deste plano cortar o eixo b na parte negativa, o índice k será negativo conforme mostra a Figura 4.
Desta maneira, as formas apresentadas na Figura 2 podem ser interpretadas como conjuntos de Células Unitárias cortadas por planos identificados pelos Índices de Miller.
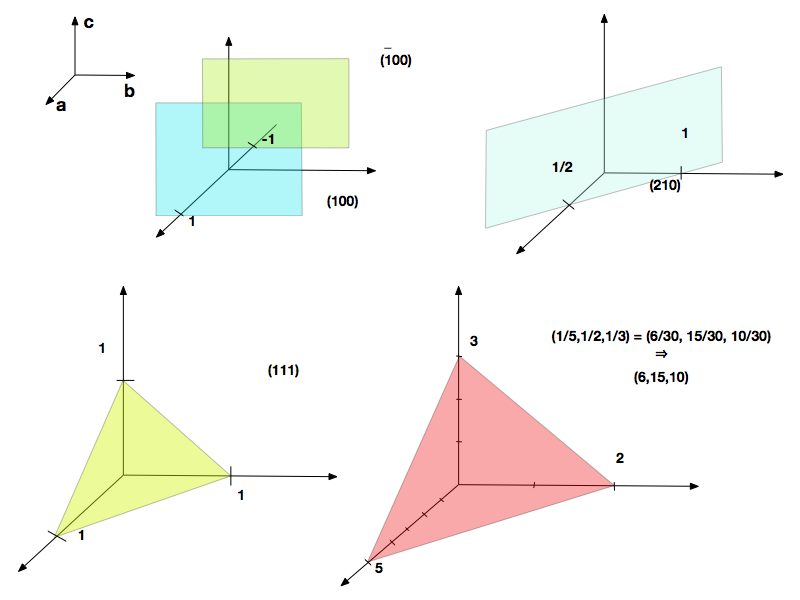
Apenas como ilustração, a Figura 5 apresenta alguns planos com seus respectivos Índices de Miller.
Observa-se que os índices permanecem números inteiros quando cortam os eixos em distâncias inferiores a 1 e deveriam ser números fracionários no caso de cortarem os eixos em distâncias superiores a um. Neste segundo caso, os índices passariam a ser números decimais com muitos algarismos significativos. Para fugir desta questão, determina-se o MMC dos índices fracionários e utiliza-se apenas os numeradores como índice, conforme mostra o plano rosa da Figura 5.
Direções
Conforme veremos no capítulo Classes Cristalinas, a identificação de direções e coordenadas torna-se necessária na Cristalografia.
Até agora, sempre foi possível utilizar o sistema de referência ortogonal a,b,c para definir os planos cristalinos. Contudo, isto nem sempre ocorre.
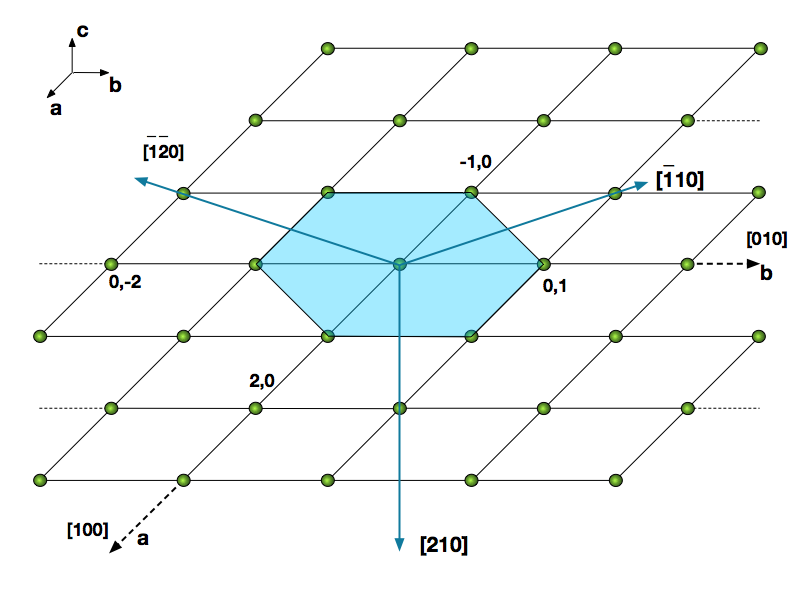
Por exemplo, a Figura 6 apresenta o plano (000)3 de uma rede cristalina tridimensional formada pelos pontos verdes montada no sistema de referência abc. Considerando o cristal hexagonal, representado pelo hexágono azul na Figura 6, torna-se conveniente definir as direções dos vetores azuis. Para isso, utiliza-se o parênteses -[]- delimitando as coordenadas da direção ou vetor. A notação do novo sistema de coordenadas, formado pelos três vetores azuis, utiliza os símbolos menor e maior – <>- para simplificar a notação, no caso <210>4 .