A Célula Unitária também se caracteriza por possuir o menor volume de todas as células, mas existem diferentes possibilidades de escolha para os Eixos Primitivos e Células Unitárias.
Existe sempre um ponto da rede cristalina em cada Célula Unitária, consequentemente, como o paralelepípedo possui oito vértices, cada célula compartilha seus vértices com oito outras células.
A partir da Célula Unitária pode-se criar os seguintes grupos geométricos distintos que satisfazem às condições estabelecidas:
-
- Triclínico;
- Monoclínico;
- Ortorrômbico;
- Tetragonal;
- Trigonal;
- Hexagonal;
- Cúbico.
A Tabela 1 apresenta as restrições e características dos Sistemas Cristalinos Primitivos em ordem crescente de simetria. Apesar de ainda não sabermos o significado dos símbolos na coluna de simetria, ela encontra-se presente porque a simetria determina a classificação do sistema e as restrições são consequência porque as restrições não formam relações biunívocas com os sistemas cristalinos.
Tabela 1. Sistema Cristalinos
| wdt_ID | Sistema | Restrições nas Dimensões | Restrições nos ângulos | Simetria Máxima |
|---|---|---|---|---|
| 1 | Triclínico | nenhuma | nenhuma |  ̄1 |
| 2 | Monoclínico | nenhuma | α=γ=90º | 2/m |
| 3 | Ortorrômbico | Nenhuma | α=β=γ=90º | mmm |
| 4 | Tetragonal | a=b | α=β=γ=90º | 4/mmm |
| 5 | Trigonal | a=b | α=β=90º, γ=120º |  ̄3 |
| 6 | Hexagonal | a=b | α=β=90º, γ=120º | 6/mmm |
| 7 | Cúbico | a=b=c | α=β=γ | m ̄3m |
Exemplo 1
Considerando um cristal com os seguintes parâmetros: a=b=12Å, c=11.9 Å, e α=β=γ= 90°, determine seu sistema cristalino.
Por eliminação, os sistemas Cúbicos, Hexagonal, e Trigonal não se aplicam porque exigem dimensões iguais, ou ângulos diferentes. Portanto, este cristal pode pertencer a qualquer sistema entre o Triclínico e o Tetragonal, uma vez que as informações fornecidas não permitem determinar exatamente a classe.
Triclínico
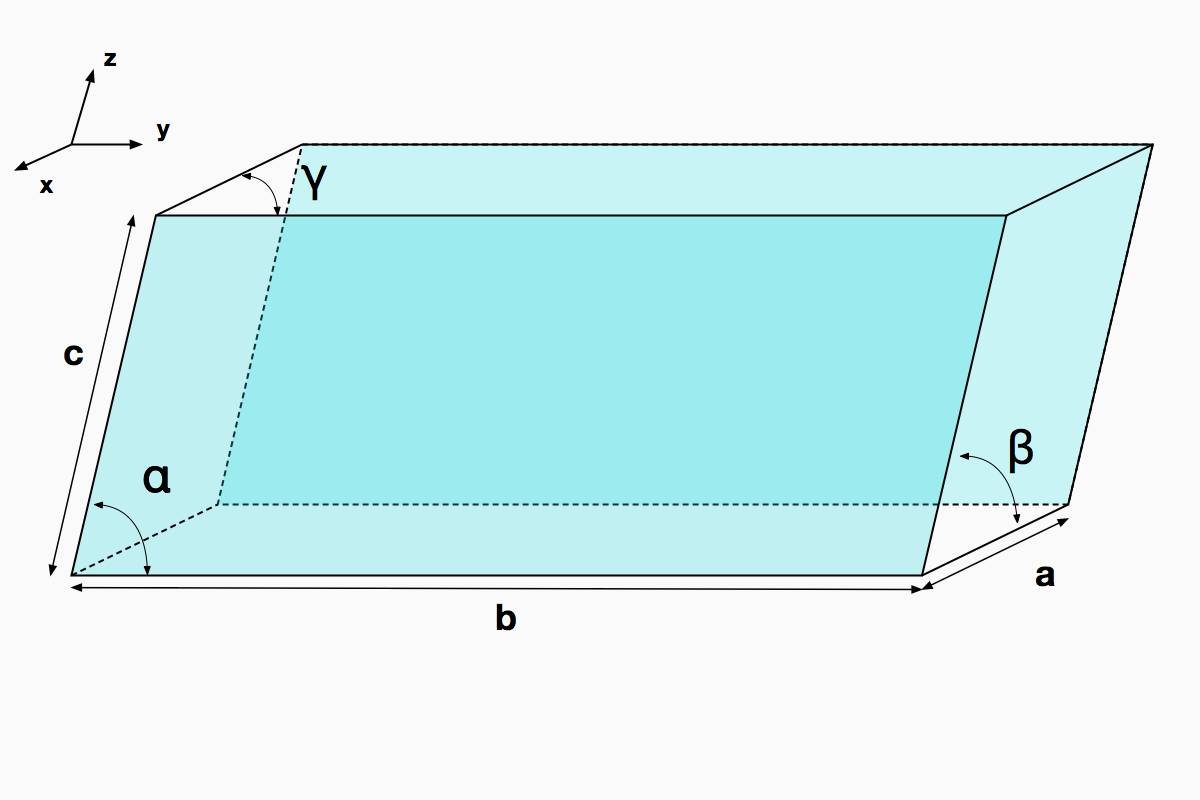
O paralelepípedo mais geral forma o primeiro grupo, chamado de Triclínico -Figura 1 – porque possui lados e ângulos diferentes.
Em todos os diagramas a seguir, os vértices representam o centro de átomos ou moléculas na estrutura cristalina. Exemplos de minerais deste sistema encontram-se em www.mindat.org.
Monoclínico
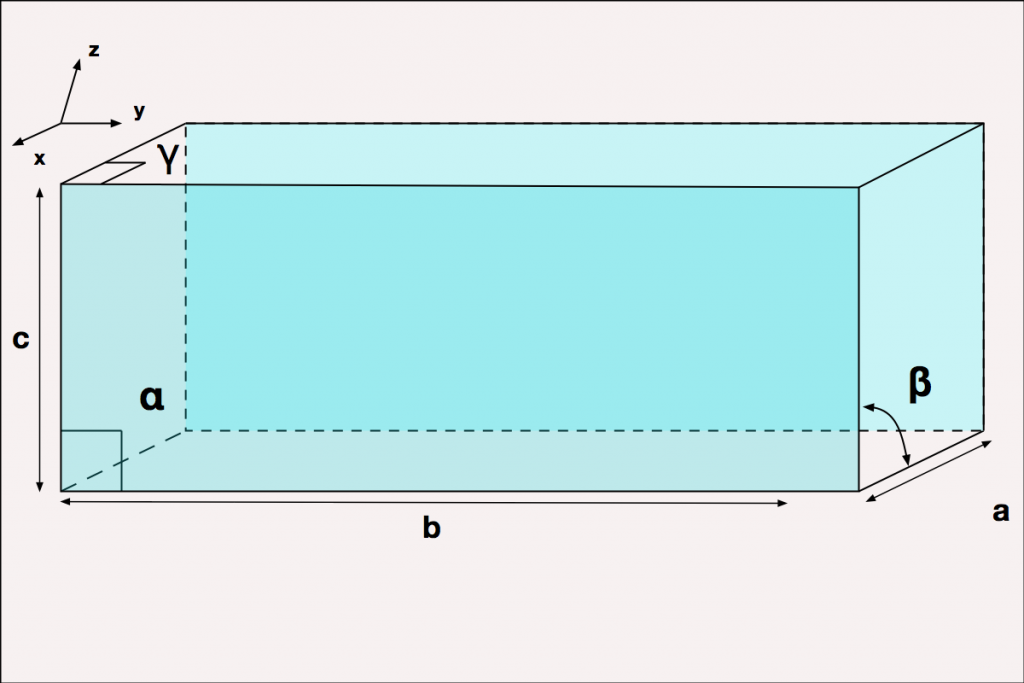
O Cristal Monoclínico – Figura 2 – representa a primeira simplificação estrutural e se caracteriza por dois ângulos retos e o terceiro qualquer.
Ortorrômbico
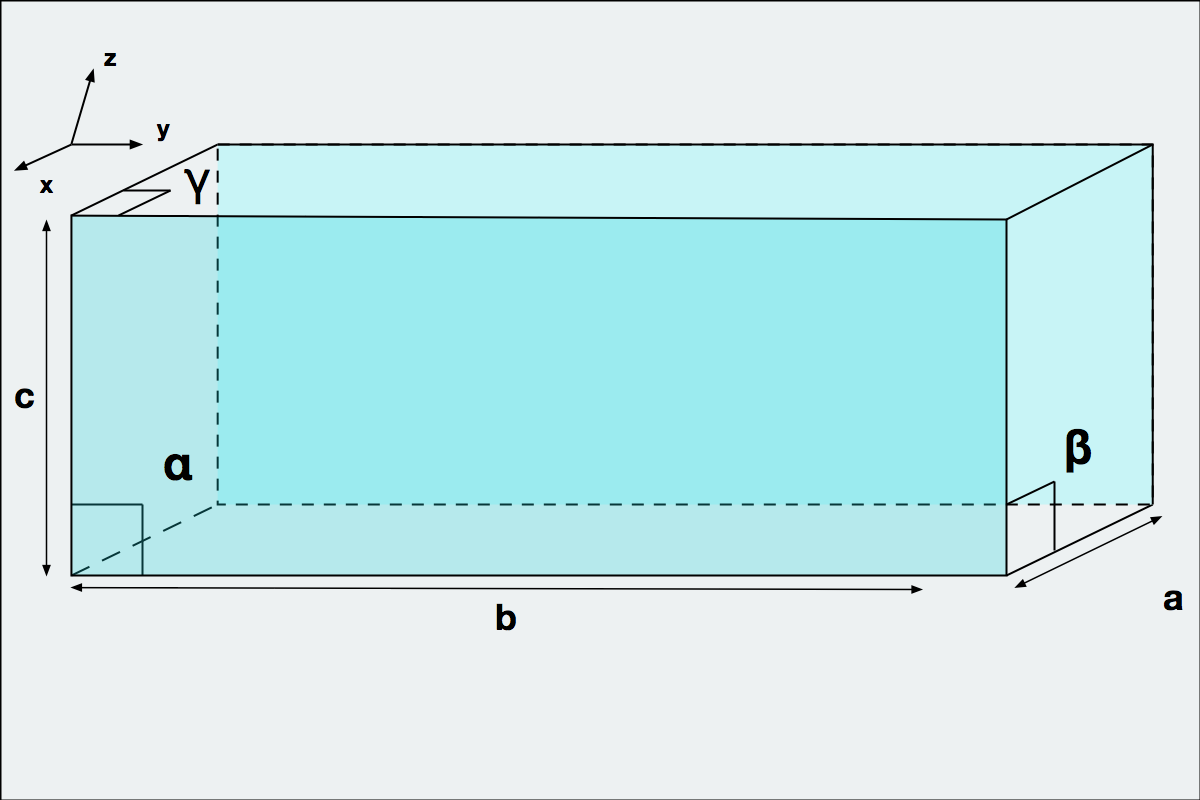
Na segunda simplificação, o grupo se denomina Ortorrômbico -Figura 3, possui todos os ângulos retos e lados distintos.
Tetragonal
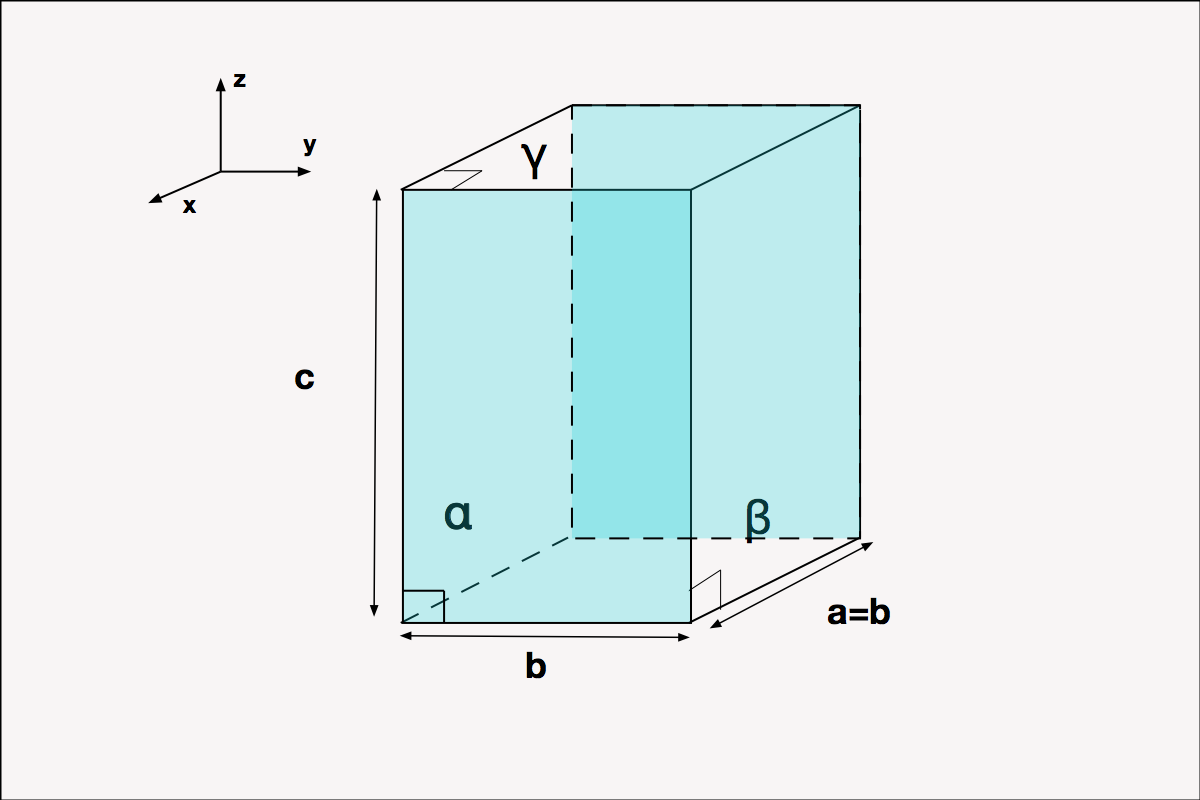
Na quarta simplificação, denominada de Tetragonal – Figura 4, o grupo possui todos os ângulos retos e dois lados iguais.
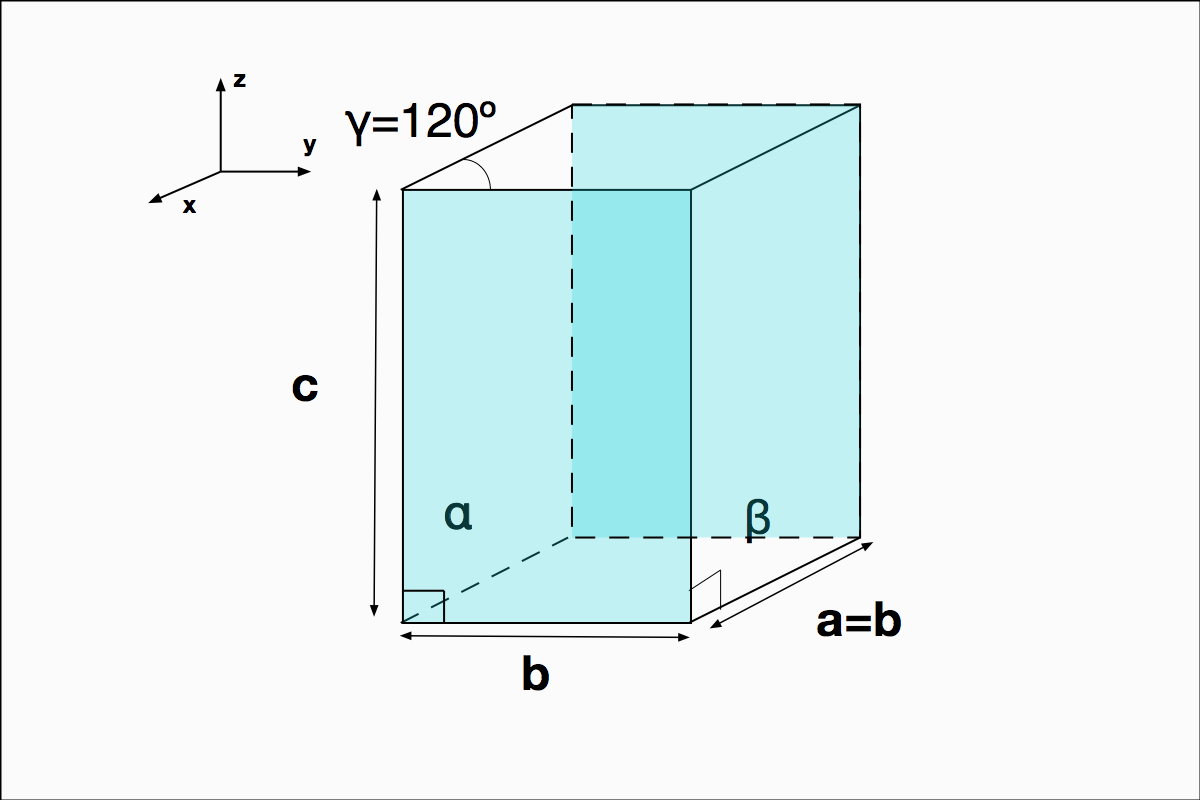
Trigonal
O Trigonal – Figura 5, possui dois ângulos retos, dois lados iguais, o outro ângulo com 120 graus e o outro lado diferente.
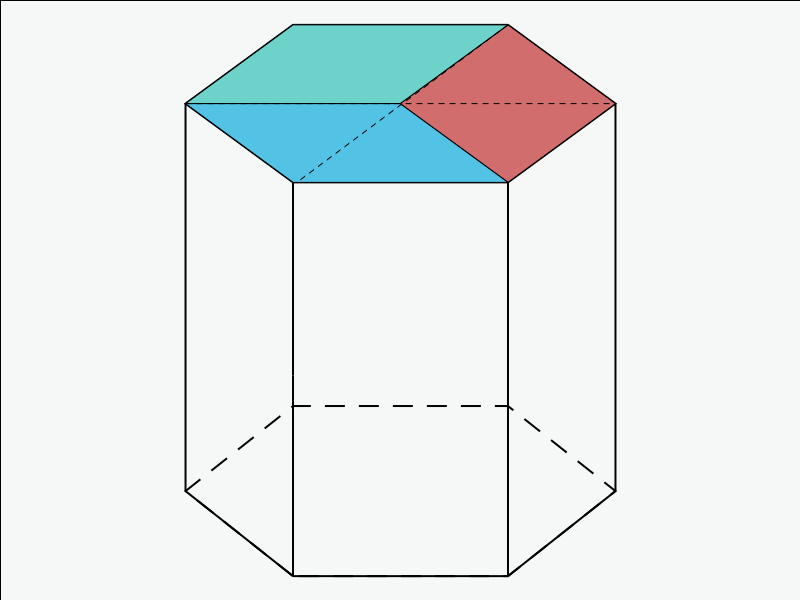
Hexagonal
O sistema Hexagonal – Figura 6 – foge um pouco da lógica de todos os outros sistemas, que se baseiam no paralelepípedo original.
Contudo, com um pouco de esforço, podemos perceber que três cristais Trigonais defasados de 120 graus em relação ao eixo central formam o sistema Hexagonal. Por isso, ambos possuem as mesmas restrições, conforme mostra a Tabela 1.
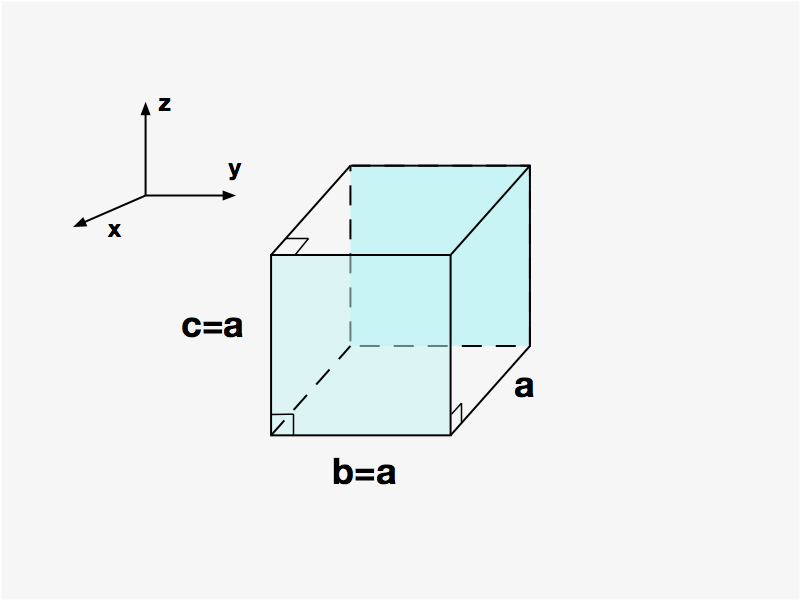
Cúbico
Finalmente, no sistema Cúbico – Figura 7, todos os lados e ângulos são iguais, sendo que os ângulos são retos, e consequentemente consiste no sistema mais simétrico de todos.
A maioria dos compostos orgânicos e inorgânicos são feitos de cristais com pouca simetria, porém os metais apresentam elevado grau de simetria e, por isso, a maioria apresenta simetria cúbica.
A Figura 8 apresenta a distribuição dos tipos de cristais nas substâncias Inorgânicas e a Figura 9 nas orgânicas.
Observa-se que o cristal Ortorrômbico predomina em todas as substâncias, seguido do Triclínico tanto para orgânicos como para inorgânicos.
Contudo, o cristal cúbico surge em terceiro lugar nos inorgânicos e o tetragonal nos orgânicos.
Figura 8. Distribuição dos cristais inorgânicos
Figura 9. Distribuição dos Cristais Orgânicos
Referências
- QUINN, J.J., TI K.S., Solid State Physics – Principles and Modern Applications, Springer-Verlag, 2009.
- NEWNHAM, R.E., Properties of Materials – Anisotropy, Symmetry, Structure, Oxford University Press, 2005.
- KITTEL, C., Introduction to Solid State Physics, Wiley, 2005.
- ASHCROFT,N.W., MERMIN, D., Solid State Physics, Harcourt, 1976.
