“Deus controla o eletromagnetismo pela teoria das ondas nas segundas, quartas e sextas-feiras, e o Diabo o controla pela teoria quântica na terça, quinta e sábado”.
Sir William Bragg – Físico Britânico
A equação de Schrödinger consiste na equação diferencial parcial que descreve a função de onda da mecânica quântica. Porém, entre Bohr e Schrödinger muita coisa aconteceu.
Conforme visto anteriormente, Planck propôs, ao estudar a radiação térmica, que a emissão de luz ocorria em quantidades discretas de energia.
Logo a seguir em 1905, Einstein 1 expandiu este conceito afirmando que a luz também se propagava, era absorvida e emitida em quantidades discretas de energia. Planck recebeu o Prêmio Nobel de Física em 1918 e Einstein em 1921.
A Equação 1 sintetiza o conceito revolucionário de que a energia da luz se tornou discreta com degraus iguais à constante de Planck.
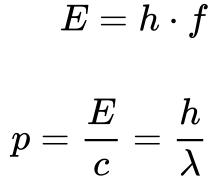
Onde:
-
- E é a energia;
- h é a constante de Planck;
- f é a frequência;
- p é o momento;
- c é a velocidade da luz;
- λ é o comprimento de onda.
De Broglie
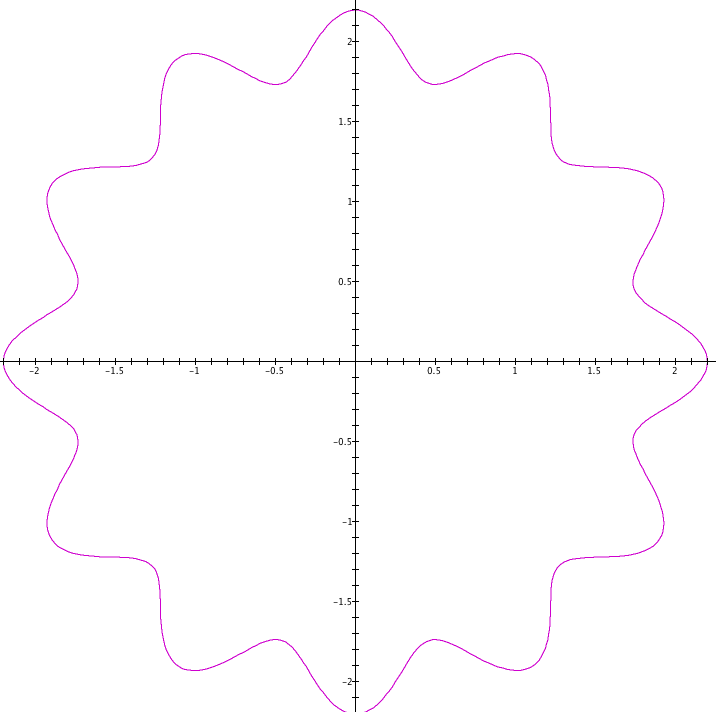
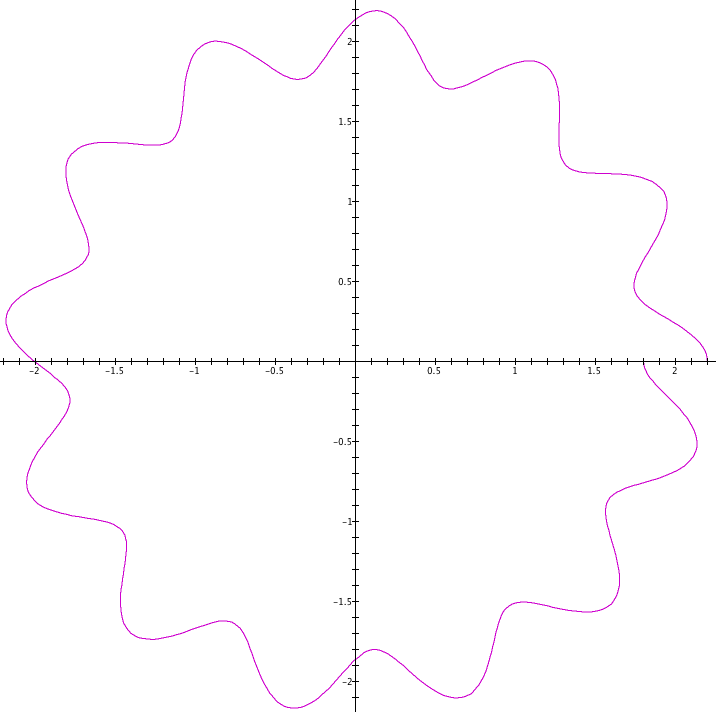
Louis de Broglie2 deu um passo à frente ao estender aos elétrons o comportamento de ondas, até então restrito à luz. As figuras 1 e 2 mostram a ideia de substituir a partícula por uma onda.
Ondas podem permanecer estáveis em orbitais, mas isto não ocorre com qualquer frequência. O número de ciclos da onda necessita ser múltiplo inteiro do caminho percorrido para que seja uma onda estacionária. Se isto não ocorrer, aparece uma descontinuidade na onda, que a torna instável.
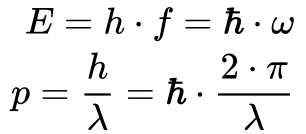
Onde:
-
- E é a energia do elétron;
- λ é o comprimento de onda do elétron;
- h é a constante de Planck;
- h cortado é a constante de Planck dividida por 2π;
- p é o momento do elétron.
Schrödinger
A Equação 3 representa uma onda unidimensional.
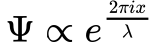
Este tipo de onda se origina de uma equação diferencial tipo Helmholtz. No caso de coordenadas cartesianas, a solução desta equação consiste numa função senoidal.
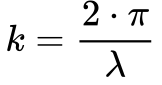
Onde:
-
- ψ é a função de onda;
- ∇2 é o operador Laplaciano3;
- k é o autovalor da equação ou número de onda.
Aplicando a Equação 1 na Equação 4, teremos que:
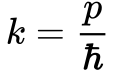
Substituindo a Equação 5 na Equação 4 e dividindo todos os termos por duas vezes a massa da partícula obtem-se a seguinte expressão:
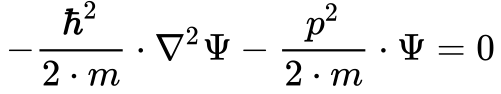
Onde:
-
- m é a massa da partícula;
- p é o momento da partícula;
- h cortado é a constante de Planck dividida por 2π;
- ψ é a função de onda.
O fator do segundo termo da Equação 6 representa a energia cinética da partícula. Como a soma da energia cinética e potencial fornece a energia total do sistema, pode-se transformar a Equação 6 na Equação 7, denominada de Equação de Schröndiger invariante no tempo. 4
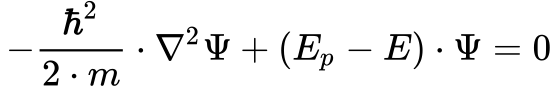
Onde:
-
- Ep é a energia potencial da partícula;
- E é a energia total da partícula.
Em 1926, Erwin Schröndinger publicou sua famosa equação que passou a representar, para a mecânica quântica, o que a segunda lei de Newton significa para a mecânica clássica. Ele ganhou em conjunto com Dirac o prêmio Nobel de Física em 1933.
Função de onda
As leis de conservação são extremamente fortes e poderosas e, por isso, os cientistas procuram sempre encontrar novas teorias que as respeitem. A conservação da energia e do momento representam casos particulares destas leis.
A solução da equação de Helmholtz5 já previa uma função de onda Ψ 6. Contudo, a grande contribuição de Schrödinger consistiu em definir uma equação de ondas planas com a energia total do sistema e sua energia potencial.
Porém, não existe uma dedução para esta equação porque ela foi postulada assim como diversas outras coisas na mecânica quântica.
Mas qual o significado físico da função de onda – Ψ(r)?
No caso da Equação invariante no tempo, a função de onda depende apenas da posição – r – da partícula.
Portanto, o quadrado do módulo desta função representa a probabilidade da partícula se encontrar próxima ao ponto r.7
Na verdade, as soluções da Equação 7 dependem de um conjunto de números discretos, denominados de números quânticos, que determinam as características dos orbitais dos Elétrons nos Átomos e, matematicamente, são os autovalores da equação.
Esses quatro números n, l, ml e ms caracterizam os orbitais dos elétrons nos átomos, mas apenas os três primeiros resultam da Equação de Schröndiger.8
O último, momento magnético do Spin possui uma outra origem.
Número Quântico Principal
O número – n, denominado de Principal, determina a energia do orbital do Elétron e representa as linhas da Tabela Periódica, que variam de 1 a 7.
Bohr já havia previsto este número em sua teoria, mas os demais números quânticos não. Adicionalmente, a Tabela Periódica de Mendelev considerava esse número de forma empírica.
Número Quântico Azimutal
O segundo número – l, denominado de número quântico azimutal ou angular, descreve o momento angular do Elétron e varia entre 0 e n-1. Ele descreve o tipo de órbita e subnível dos Elétrons no Átomo, podendo variar entre 0 e 6.
É importante observar que os três primeiros números quânticos se encontram relacionados porque representam os autovalores da Equação de Schrödinger.
A Equação 8 determina o momento angular dos Elétrons.
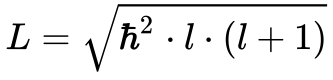
Onde:
-
- L é o momento angular dos Elétrons;
- h cortado é constante de Planck dividida por 2π;
- l é o número quântico azimutal.
Como este número quântico se encontra relacionado ao número quântico principal, a camada eletrônica n=1 possui apenas a configuração s, a camada n=2 possui apenas as configurações s e p, a camada n=3 as configurações s, p e d, e a camada n=4 as configurações s, p, d e f.
A Química já havia descoberto isso experimentalmente através da análise espectral dos elementos químicos e as denominou de Sharp, Principal, Difusa e Fundamental.
Por razões históricas, esta denominação prevaleceu.
Porém, os níveis seguintes, que não possuíam denominação clássica, receberam a designação de g, h e i seguindo a ordem alfabética a partir de f.
Este número quântico, possui grande influência na Ciência dos Materiais porque determina a forma do orbital dos Elétrons nos Átomos e, consequentemente, influencia as ligações químicas e os ângulos dessas ligações.
Número Quântico Magnético
O Número Quântico Magnético – ml – diferencia os orbitais dentro das subcamadas e varia entre -l e l, incluindo o zero.
Por isso, as subcamadas possuem quantidades crescentes de orbitais conforme mostra a Figura 3 e a Tabela abaixo.
Observa-se nesta Figura que somente a subcamada s possui simetria esférica.
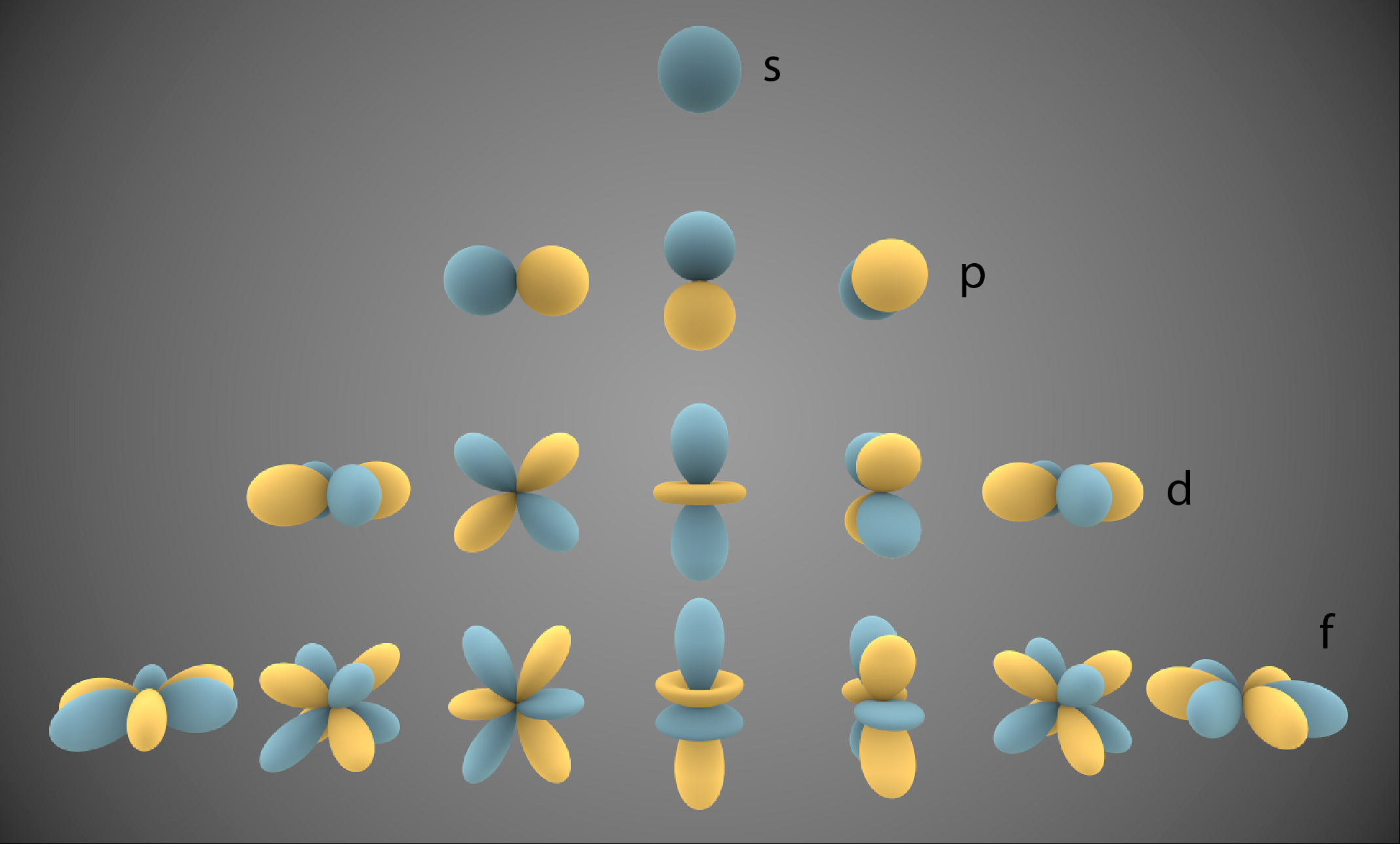
Além disso, o aumento da quantidade de Elétrons nas subcamadas equivale à quantidade de valores possíveis para l multiplicado por dois, a quantidade de spins possíveis dos Elétrons.
Números Quânticos
| wdt_ID | Orbital | Momento Angular l | Momento Magnético ml | Número de Elétrons nas Subcamadas |
|---|---|---|---|---|
| 1 | s | 0 | 0 | 2 |
| 2 | p | 1 | -1,0,1 | 6 |
| 3 | d | 2 | -2,-1,0,1,2 | 10 |
| 4 | f | 3 | -3,-2,-1,0,1,2,3 | 14 |
| 5 | g | 4 | -4,-3,-2,-1,0,1,2,3,4 | 18 |
Spin
O Número Quântico Spin representa o momento angular intrínseco de determinada partícula.
Inicialmente, Uhlenbeck e Goudsmit associaram este momento angular à rotação da partícula ao redor de seu eixo. Contudo, essa explicação possui inconsistências físicas porque o Elétron e diversas partículas elementares se confundem com ondas e não há como determinar seus raios.
Por isso, o conceito do Spin se tornou abstrato e definido pela Mecânica Quântica.
Ao contrário dos números quânticos anteriores, o Spin não surgiu com a Equação de Schrödinger.
Os números quânticos apresentados anteriormente permitiam prever o espectro de emissão ocasionado pela transição de Elétrons entre as diversas posições orbitais.
Essas transições somente deveriam ocorrer quando três números mudam porque a emissão/absorção de energia eletromagnética necessita de uma mudança no dipolo eletromagnético do átomo.
Todavia, trabalhos experimentais mostraram que esta regra deixava de funcionar na presença de campo magnético externo.
Este fenômeno, descoberto em 1896, tornou-se conhecido como Efeito Zeeman. Pieter Zeeman 9 mostrou que as linhas espectrais se dividiam em diversas componentes na presença de campos magnéticos estáticos.
Em 1913, Johannes Stark 10 descobriu que o mesmo tipo de fenômeno ocorria quando átomos e moléculas sofriam a influência de campos elétricos.
Este efeito, análogo ao Efeito Zeeman, se tornou conhecido como Efeito Stark.
Somente em 1925, Wolfgang Pauli 11 propôs o quarto número quântico com dois valores possíveis que ficou conhecido como o Spin, do Elétron e de outras partículas.
Considerando este momento angular do Spin similar ao orbital, pode-se aplicar a Equação 8, conforme mostra a Equação 9.
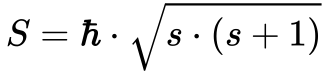
Onde:
-
- S é o momento angular do Spin;
- s é o número quântico spin;
- h cortado é constante de Planck dividida por 2π;
A Equação 10 define o Número Quântico Spin.
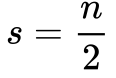
Onde:
-
- s é o Número Quântico Spin;
- n é um número inteiro positivo que inclui o zero.
O Número Quântico Spin depende do tipo da partícula, mas todos os Férmions possuem n ímpar, sendo que os elementos que formam a matéria – Próton, Neutron, Elétron, e Quarks possuem n=1.
Além disso, todos os Férmions conhecidos possuem n=1.
Por outro lado, os Bosons possuem n par, sendo que os associados às forças responsáveis pela existência da matéria – Força Eletromagnética, Força Fraca e Força Forte – possuem n=2, que resulta em s=1. Lembrando que esses Bosons são o Fóton, o Gluon, o W e o Z.
O Bóson de Higgs, recentemente descoberto, possui n=0 e nenhuma outro Bóson ainda foi encontrado com n maior que 2.
No caso dos Elétrons, o Momento Angular do Spin se caracteriza pelo número quântico s, que no caso dos Férmions vale 1/212. Desta maneira, o Momento Angular do Spin nos Elétrons vale:
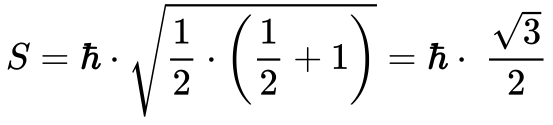
Onde:
-
- S é o momento angular do Spin;
- h cortado é constante de Planck dividida por 2π;
O Momento Angular do Spin, analogamente ao momento angular orbital, gera um momento magnético de acordo com a Equação 10.
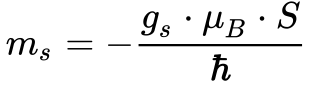
Onde:
-
- ms é o momento magnético do spin;
- gs é o fator g;
- μB é o Magneton de Bohr;
- S é o momento angular do Spin;
- h cortado é a constante de Plank dividida por 2π.
O Magneton de Bohr consiste numa constante física definida de acordo com a expressão abaixo:
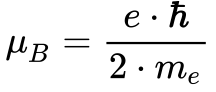
Onde:
A configuração dos Elétrons nos Átomos obedece a algumas regras básicas.
-
- Os Elétrons procuram ocupar os orbitais de menor energia. Isto significa que preferem o nível s ao p, mas quando excitados por alguma fonte de energia podem ocupar orbitais com maior conteúdo energético. Porém, o estado excitado não é estável e o Elétron tende a retornar ao orbital com menor nível energético emitindo energia- Fóton – equivalente a diferença energética dos orbitais.
- Os Elétrons ocupam orbitais com mesmo nível energético isoladamente antes de aceitarem outro Elétron. Esta regra se tornou conhecida como Regra de Hund. Hund formulou em 1927 três regras que se tornaram fundamentais para a Ciência dos Materiais.
- O maior número de Elétrons no mesmo orbital é dois, sendo que obrigatoriamente possuem spins opostos. Este é o princípio de exclusão de Pauli.
As Regras de Hund, formuladas em 1927, utilizam conceitos da Mecânica Quântica para determinar os orbitais dos Elétrons nos átomos.
- A configuração eletrônica do átomo, cujo número de Elétrons não parelhados for maior possuirá a menor energia.
- No caso de configurações com o mesmo número de Elétrons não parelhados, a configuração com maior momento orbital L possuirá a menor energia.
- No caso de átomos com menos da metade de elétrons na subcamada mais externa, o nível de menor energia corresponde ao que possuir o momento angular total (L+S) menor.
Material Complementar
Estes vídeos fornecem uma visualização interessante da função de onda e da mecânica quântica.
Referências
-
EINSTEIN, A. On a Heuristic Point of View about the Creation and Conversion of Light , Ann. Physik 17,132 (1905), translated by Haar, D. R., The Old Quantum Theory , pg. 91-107, Pergamon Press Ltd, 1967
- KREYSZIG, E. Advanced Engineering Mathematics, 9 edição, John Wiley & Sons, 2006.
- MILLER, D.A.B, Quantum Mechanics for Scientists and Engineers, Cambridge University Press, 2008.
- WOLF, H., Atomic and Quantum Physics, Springer, 1987.