“Uma medida acurada vale mais que a opinião de mil especialistas.“
Almirante Grace Hopper
Testar repetitivamente uma teoria consiste na melhor maneira de comprová-la. Porém, isso requer medições em laboratório com precisão, acurácia e resolução.
Laboratórios se tornaram os locais adequados para confirmar teorias porque possuem equipamentos de medição adequados, confiáveis e precisos. Contudo, o trabalho de laboratório requer atenção com as seguintes questões1:
-
- No que consiste medição adequada, confiável e precisa?
- Os resultados obtidos se encontram de acordo com a teoria ou um novo fenômeno foi observado?
- Os resultados encontrados podem ser reproduzidos?
Acurácia, Precisão e Resolução
Toda medição possui erro e incerteza associados porque todo instrumento afeta a grandeza medida. Portanto, trabalhos experimentais possuem erros e incertezas que necessitam tratamento apropriado para garantir a qualidade dos resultados.
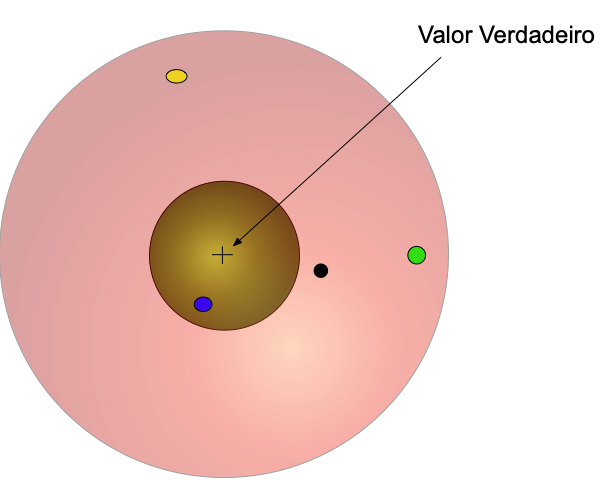
Medições possuem acurácia quando se encontram próximas do valor verdadeiro. A Figura 1 apresenta os valores medidos por quatro instrumentos diferentes (azul, amarelo, verde e preto) sendo o valor verdadeiro o centro do alvo. Neste caso, o azul apresentou melhor acurácia do que os outros porque ficou mais próximo do valor verdadeiro. Contudo, nem sempre se conhece o valor verdadeiro do que se mede.
Para resolver esta questão, calibramos os instrumentos a partir de padrões das grandezas medidas. Os padrões fornecem os valores verdadeiros para avaliarmos a acurácia do instrumento. Contudo, isto é assunto para a cadeira de Medidas e, neste curso, consideraremos os medidores calibrados.
Além da acurácia, as medições possuem precisão. Os instrumentos podem apresentar valores diferentes ao medirmos repetitivamente o mesmo valor verdadeiro.
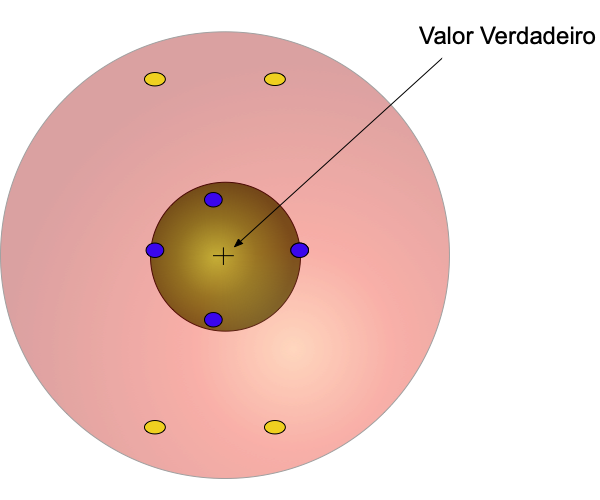
A Figura 2 mostra o conceito de precisão. Neste caso, existem apenas dois instrumentos (azul e amarelo).
Quando existem diversas medições com o mesmo instrumento, define-se acurácia como a média dos valores medidos. Neste contexto, ambos instrumentos apresentaram a mesma acurácia porque os pontos medidos se encontram simetricamente dispostos ao redor do valor verdadeiro, e, consequentemente, o valor médio dessas medidas corresponde ao valor verdadeiro em ambos os casos.
Por outro lado, calcula-se a precisão como sendo o desvio padrão entre os valores medidos com relação ao valor verdadeiro. No caso da Figura 2, o instrumento amarelo apresentou desvio maior e, consequentemente, pior precisão.
Além disso, a medição depende da escala do instrumento e do operador que a realiza. Por exemplo, um voltímetro digital apresenta um valor de 0,01 V.
Se desconhecermos maiores detalhes do funcionamento do instrumento, considera-se a precisão como sendo a menor unidade do valor apresentado, neste caso 0,01 V. Portanto, o valor medido se situa em 0,01 ± 0,0045 para levar em conta o arredondamento.
Isto significa que o valor verdadeiro se encontra entre 0,02 e 0,00 e erro relativo ao valor medido igual a ± 100%. Evidentemente, este instrumento e/ou escala se encontra inadequado para esta medição.
Este exemplo remete à questão da resolução do instrumento. A escala utilizada no instrumento não possui resolução suficiente para medir o valor em questão.
No caso de instrumentos analógicos, a resolução se relaciona à maior variação possível de ser observada pelo olho humano.
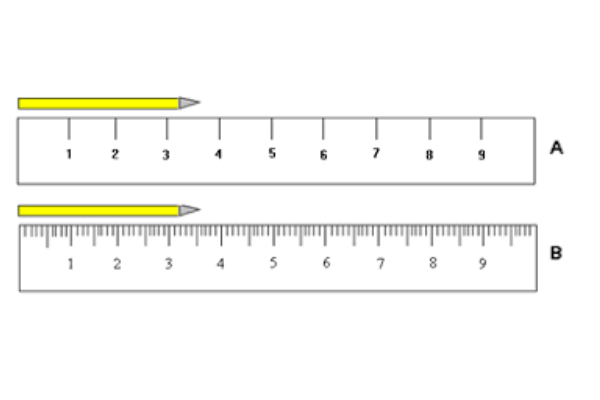
Por exemplo, a Figura 3 apresenta duas réguas medindo o mesmo lápis, garantindo-se assim o mesmo valor verdadeiro.
A precisão da régua A é de 0,5 porque estima-se visualmente meia divisão no máximo.
Por outro lado, apesar de também só ser possível estimar visualmente meia divisão, a precisão da régua B é de 0,05, porque a escala possui mais divisões.
Portanto, a régua B possui maior resolução do que a régua A.
Por isso, quanto maior a resolução do instrumento melhor a qualidade da medida, desde que tenham acurácia e precisão equivalentes.
Algarismos significativos
As seguintes regras2 auxiliam na determinação dos algarismos significativos de uma medida:
-
-
Todos os algarismos diferentes de zero são significativos;
-
Todos os zeros entre algarismos diferentes de zero são significativos:
-
Zeros à esquerda do primeiro algarismo diferente de zero não são significativos;
-
Zeros à direita do último algarismo diferente de zero e depois da vírgula são significativos;
-
Zeros à direita de números sem virgula podem ser ou não significativos.
- Números provenientes de fórmulas, números irracionais, e constantes exatas da física possuem infinitos algarismos significativos.
-
Exemplos
- 2 156 possui quatro algarismos significativos3;
- 2,156 x 103 é igual ao anterior e possui quatro algarismos significativos;
- 0,021 56 equivale a 2,156 x 10-2 e possui quatro algarismos significativos;
- 2 105 tem quatro algarismos significativos;
- 150,0 Ω é igual a 1,500 x 101 e possui quatro algarismos significativos;
- 150 Ω é igual a 1,5 x 101 e possui dois algarismos significativos. Porém, se a precisão e resolução do instrumento permitir, deve-se considerar este zero significativo. [efn_note] por isso, deve-se tomar cuidado na leitura de instrumentos para colocar a vírgula em casos semelhantes quando a resolução do instrumento permitir. [/efn_note]
- 0,150 kΩ possui três algarismos significativos e resolve a incerteza do zero ser ou não ser significativo. 4
Por isso, deve-se realizar medidas com a maior quantidade de algarismos significativos possível para manter a qualidade do experimento.
Considerando os instrumentos escolhidos, as medidas devem utilizar escalas adequadas para que as leituras ocorram próximas ao fundo de escala do aparelho.
Operações com algarismos significativos
Na engenharia, cálculos matemáticos se tornam necessários para analisar resultados de experiências ou projetar máquinas, equipamentos e instalações.
Nestes casos, como determinar os algarismos significativos dos resultados?
Multiplicação e Divisão
No caso de multiplicações e divisões o resultado deve conter o menor número de algarismos significativos dos números envolvidos. 5
Exemplos
- 4,502 x 10 = 45,02, mas como 10 possui apenas um algarismo significativo, o resultado correto é 50 em decorrência do arredondamento.
- 4,502 x 10,0 = 45,02, mas como 10,0 possui três algarismos significativos, o resultado correto se torna 45,0.
- 4,502 x 10,00 = 45,02, e este é o resultado correto porque ambos os números possuem a mesma quantidade de algarismos significativos.
- 4,502 ÷ 2,12 = 2,123584905660377, mas a resposta correta é 2,12 porque 2,12 possui três algarismos significativos e arredonda-se sempre o último.
- 4,502 ÷ 2,120 = 2,123584905660377, mas a resposta correta é 2,124 porque ambos os números possuem quatro algarismos significativos e arredonda-se sempre o último.
- 2π x 0,2 = 1,25663706144 …., mas a resposta correta é 1 porque 0,2 possui apenas um algarismo significativo.
- 2π x 2,0 = 12,5663706144 …., mas a resposta correta é 13 porque 2,0 possui dois algarismos significativos.
- 2π x 2,000 = 12,5663706144 …., mas a resposta correta é 12,56 porque 2,000 possui quatro algarismos significativos.
Soma e subtração
No caso de soma e subtração, o número de algarismos depois da vírgula determina a quantidade de algarismos significativos do resultado, sempre o menor número de algarismos significativos dentre os números das parcelas.
Exemplos
- π + 20,3 = 23,4415926….., mas o resultado correto se torna 23,4 porque o menor número de casas após a vírgula das parcelas é três.
- 1 000 – π = 996,858407….., mas o resultado correto se torna 997 porque 1 000 não possui dígitos depois da vírgula.
- 1 000,0 – π = 996,858407….., mas o resultado correto se torna 996,9 porque 1 000 possui um digito depois da vírgula.
Propagação de Erros
Existem três tipos de erros em trabalhos de medição e laboratório:
- Erros randômicos, que influenciam a precisão;
- Erros sistemáticos, que afetam a acurácia;
- Erros humanos, que inutilizam o trabalho.
Deve-se minimizar e conhecer os erros para garantir a qualidade do trabalho laboratorial.
Os manuais dos equipamentos de medição fornecem normalmente a acurácia como um percentual do valor de fundo de escala do instrumento.
Desta maneira, podemos comparar instrumentos com escalas diferentes, mas o erro percentual aumenta quando medimos valores no início da escala.
Constantes físicas necessitam do máximo de precisão, mas erros ainda existem.
A Tabela Constantes Físicas apresenta os valores, as unidades, e a incerteza das constantes mais importantes para este curso. A coluna da incerteza apresenta a palavra exata para as constantes físicas definidas, e sempre deve-se utilizá-las para garantir resultados mais precisos.
Contudo, outras constantes apresentam um número de dois algarismos entre parênteses na coluna da incerteza. Esta convenção significa que os valores possuem um erro de ± o valor em parênteses nos dois últimos dígitos da grandeza.
Exemplo
- O valor de ε0 é 8,854 187 817 8128 (13) x 10-12 [F/m], significando que o valor verdadeiro se encontra entre 8,854 187 817 8115 e 8,854 187 817 8141.
Na maioria das aplicações de engenharia esse erro é desprezível, mas a questão se torna mais complicada quando se utiliza dados medidos em funções matemáticas.
Considerando y como sendo função da variável medida x e aplicando a série de Taylor limitada à primeira derivada, teremos que:
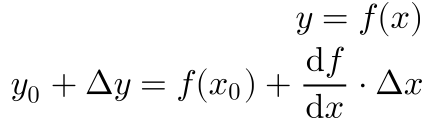
Portanto, o erro da variável y será dado por:
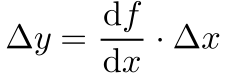
A Equação 2 mostra que a derivada da função pode amplificar ou reduzir o erro da variável.
Exemplo #1
Considerando o método do voltímetro e amperímetro para medir resistência, existem duas fontes de erro; a medida da corrente e a medida da tensão.
Neste caso, a equação 3 descreve a função F e a equação 4 fornece o erro de medição da resistência (ΔR) em função dos erros de medida de tensão (ΔV) e de corrente (ΔI).
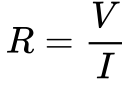
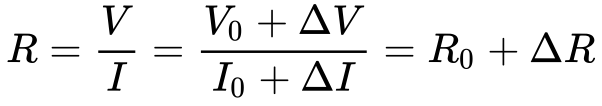
Expandindo a Equação 4, obtém-se as seguintes relações:
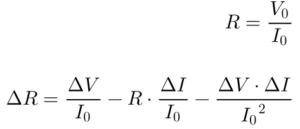
Portanto, neste caso, o erro na medida de resistência dependerá da combinação dos erros de corrente e tensão.
Problema Proposto
A partir da equação da resistividade da Equação 5, deduza a incerteza da resistividade de um fio cilíndrico apresentada na Equação 6.
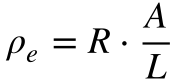
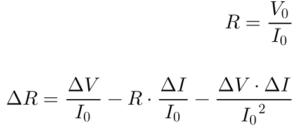
Registro de Medidas
O registro das medidas deve sempre conter a informação da medição e de sua incerteza, registrada com dois algarismos significativos.
Existem duas formas de registrar a incerteza das medições: a notação ± e a notação com parênteses.
No caso da notação ±, calcula-se a incerteza primeiro e depois se ajusta a precisão da medida. Exemplo: 4,22 ± 0,43 Ω.
A notação com parênteses consiste em uma alternativa à notação ±.
Neste caso, o exemplo anterior seria escrito da seguinte maneira 4,22(43)Ω, onde os números em parênteses representam sempre incerteza nos dois últimos dígitos do valor da medida.
Por exemplo, considerando a leitura de 4,6 V de um instrumento digital, salvo características especiais do instrumento, a leitura deve ser registrada como 4,6 ± 0,045 V.
Isto deve ser feito porque o valor verdadeiro se encontra, em função da resolução digital do instrumento (o último dígito), entre 4,64 e 4,55. 6
Por isso, a incerteza deve possuir sempre dois algarismos significativos.
Contudo, este exemplo apresenta uma simplificação.
Muitas vezes, ao repetirmos a mesma medição, com o mesmo instrumento, e nas mesmas condições, obtemos resultados diferentes. Neste caso, devemos empregar métodos estatísticos.
Erros de Medição
Os erros de medição se dividem em:
-
- Erros aleatórios ou randômicos;
- Erros sistemáticos;
- Equívocos.
Minimiza-se os erros aleatórios através de múltiplas medições e análise estatística, e a média das medidas realizadas representa a melhor estimativa do valor verdadeiro e o desvio padrão fornece a melhor estimativa da precisão 7.
Os erros aleatórios decorrem de interferências externas no experimento e/ou no instrumento de medição.
Falta de calibração e aferição de instrumentos representa a principal causa de erros sistemáticos.
Finalmente, equívocos, representam a principal fonte de erros em laboratórios escolares e são difíceis de encontrar.
Por isso, o registro cuidadoso das experiências consiste na maneira mais eficaz de evitá-los e encontrá-los.
Referências
- BERENDSEN, H. J. C., A Student’s Guide to Data an Error Analysis, Cambridge, 2011.
- MERRIN, J., Introduction to Error Analysis, CreateSpace, 2017.
- HUGHES, I. G., HASE, T. P. A., Measurements and their Uncertainties, Oxford, 2010.
- HUGHES, A. T, Measurement and Control Basics, ISA, 4 ed., 2007.
- CZICHOS, SAITO, SMITH, Handbook of Metrology and Testing, Springer, 2 ed., 2011.
- THE ORGANIC CHEMISTRY TUTOR, Operações com algarismos significativos, Youtube, <https://youtu.be/BmeImtwhfj8>