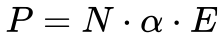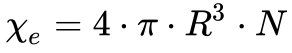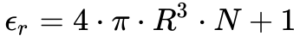“Considerações elementares me levaram à conclusão de que um meio, composto de camadas de diferentes constantes dielétricas, deve se comportar como um cristal uniaxial se for assumido que a espessura da camada é apenas uma fração do comprimento de onda.“
Os fenômenos dielétricos se revelaram ao homem na antiguidade.
Os Gregos conheciam a propriedade do Âmbar atrair pequenos objetos após friccionado com pano, e esfregar um pente no cabelo permite atrair pequenos pedaços de papel.
Contudo, somente a partir do século 18, Leyden iniciou o estudo científico desse fenômeno e Faraday, 90 anos depois, mostrou que a capacitância dependia do material no interior do capacitor.
Maxwell unificou o Eletromagnetismo em 1894 propondo o seguinte sistema de equações que uniram o magnetismo e a eletricidade, conforme mostra a Figura 1.
Materiais dielétricos perfeitos possuem apenas cargas elétricas imóveis, que são incapazes de conduzir corrente.
Porém, as cargas elétricas que constituem os materiais se movem, mesmo dentro dos sólidos.
A matéria sólida consiste basicamente em átomos e moléculas unidos por ligações químicas e arrumados em estruturas cristalinas.
As cargas elétricas da matéria sólida se distribuem nos átomos, moléculas e cristais de tal forma que, na ausência de campo elétrico externo, o “centro de gravidade” das cargas positivas e negativas coincide. Isto significa que da soma total das cargas ser zero e inexistem “momentos elétricos”.
Porém, em alguns casos, a estrutura da molécula e/ou cristal faz com que o centro de gravidade das cargas não seja o mesmo. Nesses casos, o material apresenta momento elétrico natural.
A aplicação de campo elétrico externo afeta o arranjo e o balanço dessas ligações, o que provoca uma série de fenômenos dielétricos, tais como:
-
- Ressonância elétrica;
- Relaxação elétrica;
- Armazenamento de energia;
- Dissipação de energia;
- Efeitos térmicos;
- Efeitos mecânicos;
- Efeitos óticos;
- Envelhecimento;
- Ruptura dielétrica.
Polarização Eletrônica ou Ótica
Átomos são eletricamente neutros, mas possuem cargas distribuídas espacialmente em seu interior de acordo com a mecânica quântica. Contudo, pode-se representar o núcleo do átomo por uma carga positiva e os elétrons por outra carga negativa de mesmo valor absoluto.
A Figura 2 mostra que a ação do campo elétrico (E) nos átomos ocasiona uma distorção na configuração espacial dos elétrons que se assemelha ao alinhamento de um dipolo elétrico submetido ao mesmo campo.
Esta distorção ocorre basicamente nas camadas mais externas de elétrons e se denomina de Polarização Eletrônica ou Polarização Ótica. 1
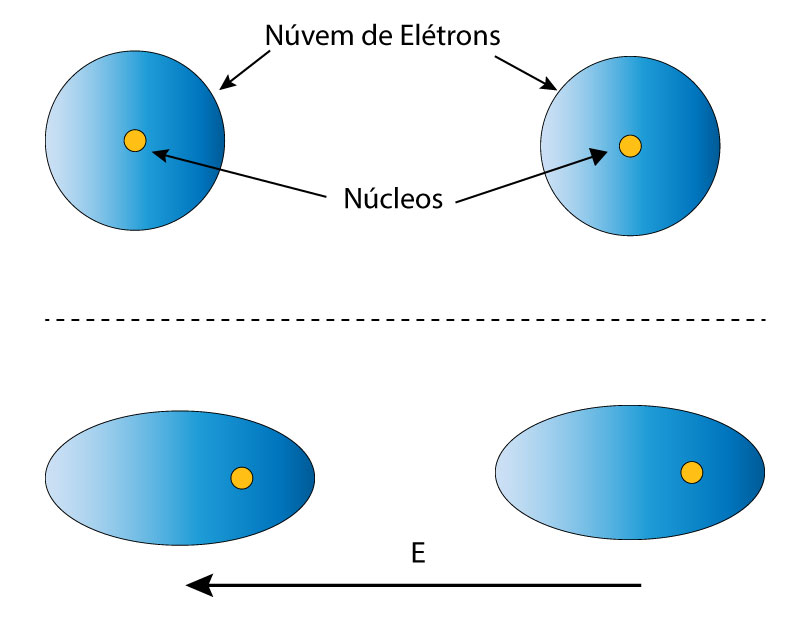
De acordo com Raju, pode-se estimar a polarização eletrônica considerando a carga dos elétrons distribuída uniformemente numa esfera de raio R e as cargas positivas concentradas no centro.
O campo elétrico aplicado gera um deslocamento nos centros de gravidade das cargas e, com isso, cria um dipolo elétrico.
De acordo com Raju, esse deslocamento é dado por:
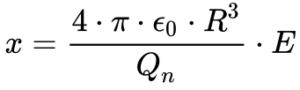
Onde:
-
- R é o raio da esfera ou do átomo;
- Qn é a carga elétrica do núcleo;
- E é o campo elétrico.
Por sua vez, esse deslocamento das cargas produz um momento na esfera dado de acordo com:
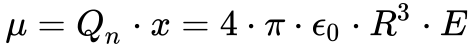
Onde:
-
- μ é o momento do dipolo elétrico induzido pelo campo elétrico.
Como esse momento depende do campo elétrico externo, torna-se desejável normalizá-lo com relação ao campo elétrico para que se tenha uma grandeza que dependa apenas do material.
Por isso, define-se a polarizabilidade do material como sendo:
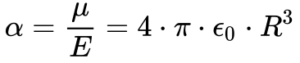
Onde:
-
- α é a polarizabilidade do material [F.m2] 2;
- R é o raio do átomo[m].
Polarização Iônica ou Molecular
Substâncias sólidas formadas por ligações iônicas apresentam estruturas cristalinas conforme mostra a Figura 3.
Sem a presença de campo elétrico, os dipolos se cancelam e o valor resultante é nulo.
Contudo, a aplicação de um campo elétrico externo altera a posição dos íons criando um dipolo elétrico resultante.
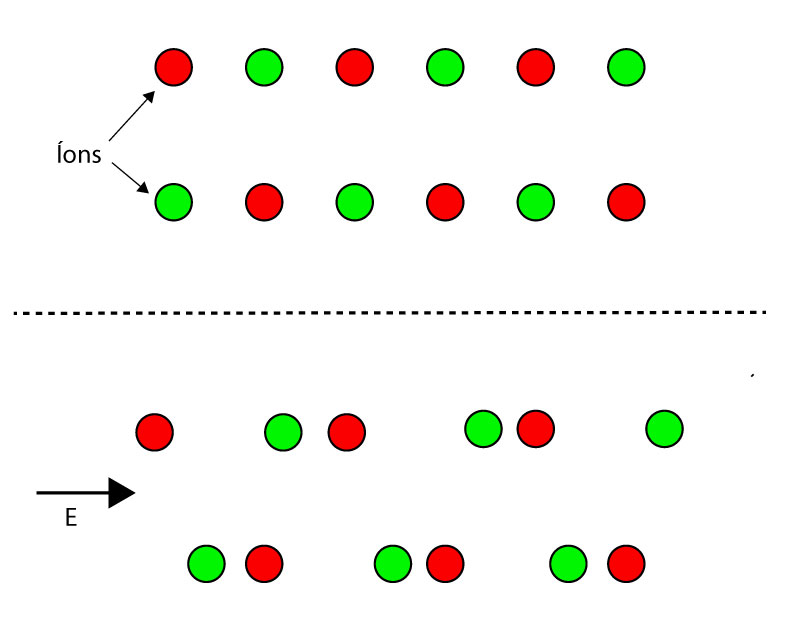
Os íons dos átomos apresentam aproximadamente a mesma polarizabilidade dos átomos que possuem a mesma quantidade de elétrons que os íons.
Por exemplo, o íon de Sódio – Na+ – apresenta polarizabilidade próxima a do Neon – Ne.
Deve-se observar que toda a teoria apresentada se baseia na distribuição esférica dos elétrons. Quando se considera a real distribuição espacial dos elétrons, a polarizabilidade se transforma num tensor.
Polarização de Orientação
Comportamento similar ocorre com moléculas que possuem dipolos elétricos. Contudo, a análise desse mecanismo requer um aperfeiçoamento dos modelos.
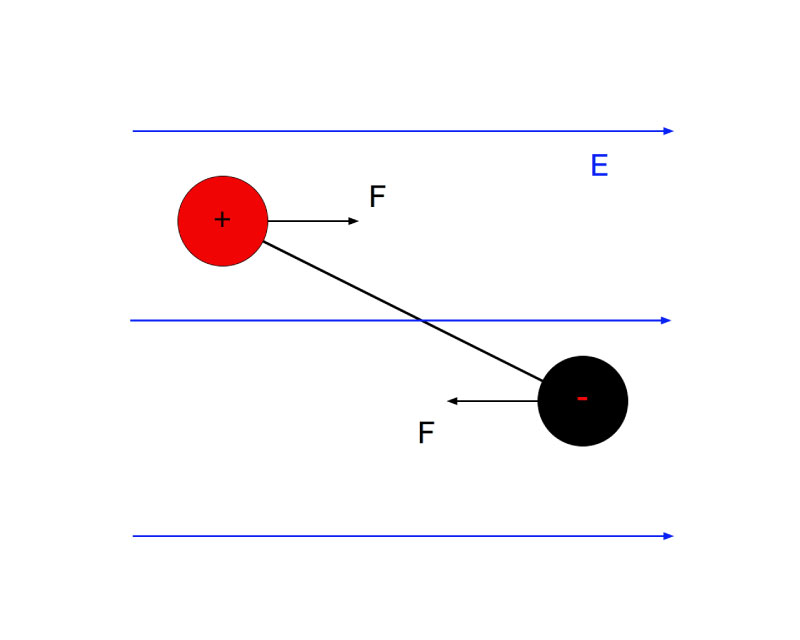
A Figura 4 apresenta um modelo simplificado do dipolo elétrico.
Duas cargas de polaridade opostas conectadas por forças que as mantêm separadas de determinada distância formam um dipolo elétrico.
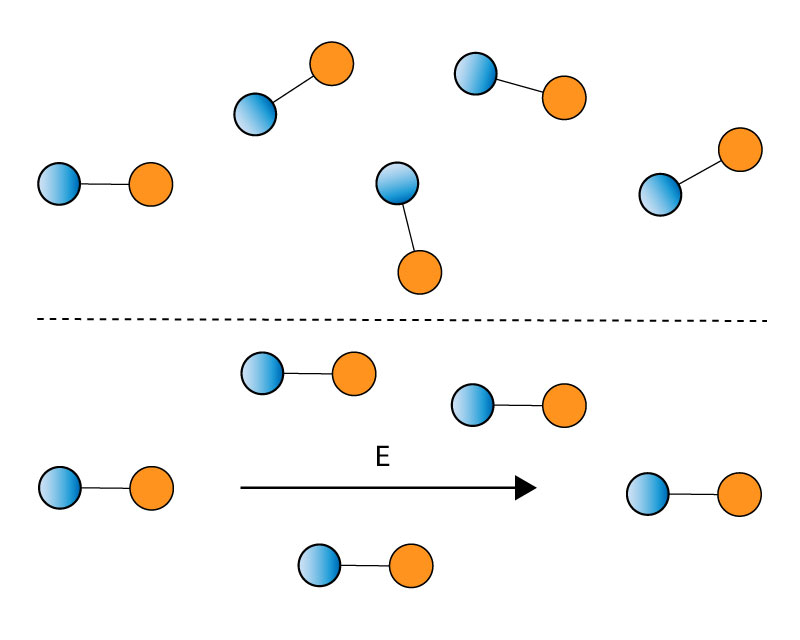
A Figura 5 apresenta o comportamento de materiais que possuem dipolos elétricos quando submetidos a um campo elétrico.
A existência de dipolos elétricos no dielétrico e suas orientações pelo campo elétrico forçam o aparecimento de cargas adicionais3 nas placas para manter a neutralidade das cargas.
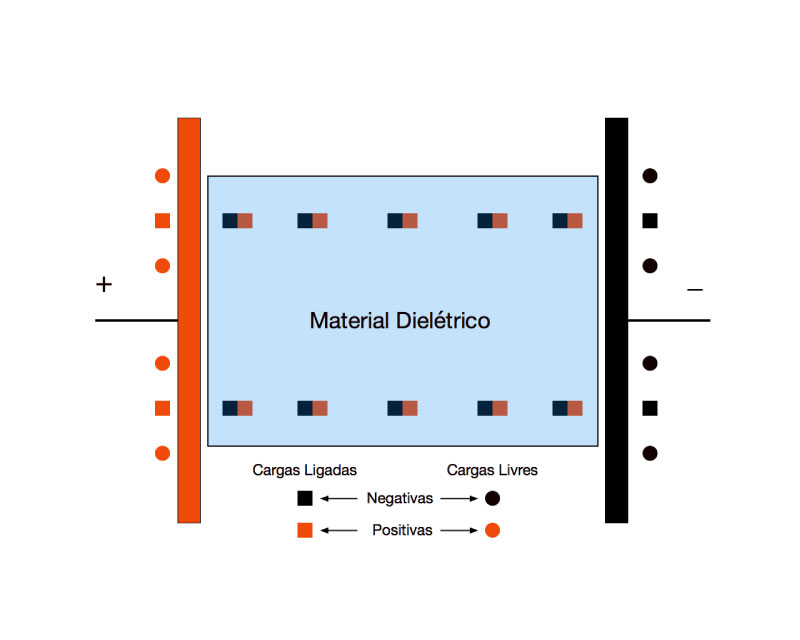
Denomina-se este fenômeno de Polarização de Orientação, conforme mostra a Figura 6.
Por exemplo, as moléculas de água apresentam um dipolo elétrico natural que se orienta de acordo com o campo elétrico aplicado.
Portanto, nos materiais dielétricos, o campo elétrico externo produz um alinhamento das cargas elétricas existentes no material, modificando assim o campo elétrico no seu interior.
Moléculas possuem polarizabilidade maiores do que a dos átomos e íons porque a nuvem de Elétrons é maior e podem ser mais facilmente deslocadas.
Essa facilidade de deslocamento ocorre porque as forças envolvidas nas ligações químicas são mais fracas do que as forças das ligações atômicas.
Além disso, existem dois outros mecanismos de polarização: a Polarização Espontânea e a Polarização de Interface ou de Carga Espacial.
Consequentemente, a combinação de todos os tipos de polarização apresentados determina a polarização final dos materiais, sendo que a Polarização Espontânea se encontra presente apenas nos materiais Ferroelétricos.
Metais
O comportamento muda nos metais. Como os elétrons possuem liberdade de movimento, o campo elétrico provoca uma concentração superficial de cargas que anula o campo elétrico no interior do material. Portanto, o campo elétrico no interior dos metais é sempre nulo.
A Polarização Eletrônica, mostrada na Figura 2, ocorre em todos os materiais, e os outros ocorrem dependendo do tipo de material envolvido.
Outro aspecto importante consiste na diferença de massas e forças envolvidas nos quatro casos.
Como a massa dos elétrons é muito pequena, a polarização elétrica ocasionada por eles responde a campos elétricos de alta frequência até a luz visível.
Por outro lado, como os íons possuem muito mais massa do que os elétrons, a polarização iônica se torna sensível até frequências próximas ao infravermelho.
Seguindo este raciocínio, como as moléculas pesam mais que os íons, a polarização ocorre apenas com variações de campo elétrico com frequências inferiores a micro-ondas.
Finalmente, a polarização causada pela carga espacial responde até a frequência de quilohertz.
O vetor polarização se relaciona com polarizabilidade da seguinte maneira:
Onde:
-
- P é o vetor polarização;
- α é a polarizabilidade do material;
- N é a densidade de dipolos elétricos do material.
- E é o campo elétrico.
Substituindo P, dado pela equação 5, e α, dado pela equação 3, na equação 7 obtemos que:
Aplicando a Equação 6, obtemos a constante dielétrica relativa do material como sendo igual a:
Fonte: Matweb
Material Símbolo Rigidez Dielétrica[kV/mm] Constante Dielétrica Relativa Observações Fator de dissipação
Bromo Br 3,15
Selênio Se 6,60
Alumina Al2O3 9,00 9,3
Quartzo SiO2 4,2
Baquelite Sumitomo Durez 22257 7,9 5,5 @ 1 MHz 0,08
Germanium Ge 16
Silício Si 11,8
Estanho Sn 24
Metanol 32,63
Etanol 24,3
PPA com fibra de vidro 0.8 a 37,0 3,59 a 136 varia com a frequência e temperatura 0,005 a 0,85
Água H2O 55,51 a 87,9
80.2 @20Cvaria com a temperatura e pressão
Água Pesada D2O 78,06 @ 20C
Titanato de Bario BaTiO3 1000 a 5000
Referências
- AGILENT TECHNOLOGIES, Basics of Measuring the Dielectrics Properties of Materials – Application Note,
- KAO, K.C., Dielectric Phenomena in Solids, Elsevier, 2004.
- PEEK, F. W., Dielectric Phenomena in High Voltage Engineering, McGraw-Hill, 2 ed., 1920.
- RAJU, G. G., Dielectrics in Electric Fields, Dekker, 2002.
- SOLYMAR, L., WALSH, D., SYMS, R. R. A., Electrical Properties of Materials, Oxford, 10 ed., 2019
- VON HIPPEL, A. R., Dielectrics and Waves, MIT, 1954.