“A descoberta do Quantized Hall Effect (QHE) foi o resultado de medições sistemáticas em transistores de efeito de campo de silício – o dispositivo mais importante da microeletrônica.”
Em 1879, Edwin Herbert Hall descobriu aos 24 anos, durante seu trabalho de doutorado1, um estranho comportamento em condutores elétricos, que ficou conhecido como Efeito Hall.
Essa descoberta ocorreu 18 anos antes da descoberta do Elétron em 1897, e, naquela época, ainda se considerava a corrente elétrica um fluido contínuo.
Contudo, somente a partir de 1968 as primeiras aplicações práticas surgiram com o lançamento do primeiro teclado em estado solido para computadores que utilizava sensores de Efeito Hall. Pela primeira vez, o sensor e o circuito eletrônico auxiliar se encontravam no mesmo circuito integrado.
Atualmente, os sensores de Efeito Hall integram diversos equipamentos, desde computadores, celulares, máquinas de costura, automóveis, aviões, ferramentas e equipamentos médicos. Adicionalmente, eles se tornaram a tecnologia mais utilizada para detectar campos magnéticos2.
Porém, mais uma vez, a Física Quântica trouxe novos avanços teóricos. Em 1980, Klaus von Klitzing descobriu o comportamento quântico do Efeito Hall e ganhou o Prêmio Nobel de Física de 1985 por essa descoberta.
Efeito Hall
Ao estudar a força provocada pelo campo magnético em fios conduzindo corrente elétrica – Figura 1, Hall questionou se a força atuava no fio ou apenas nas cargas elétricas em movimento dentro do fio.
A dúvida procede porque como não existe força no fio sem corrente, a força deve depender de outra coisa.
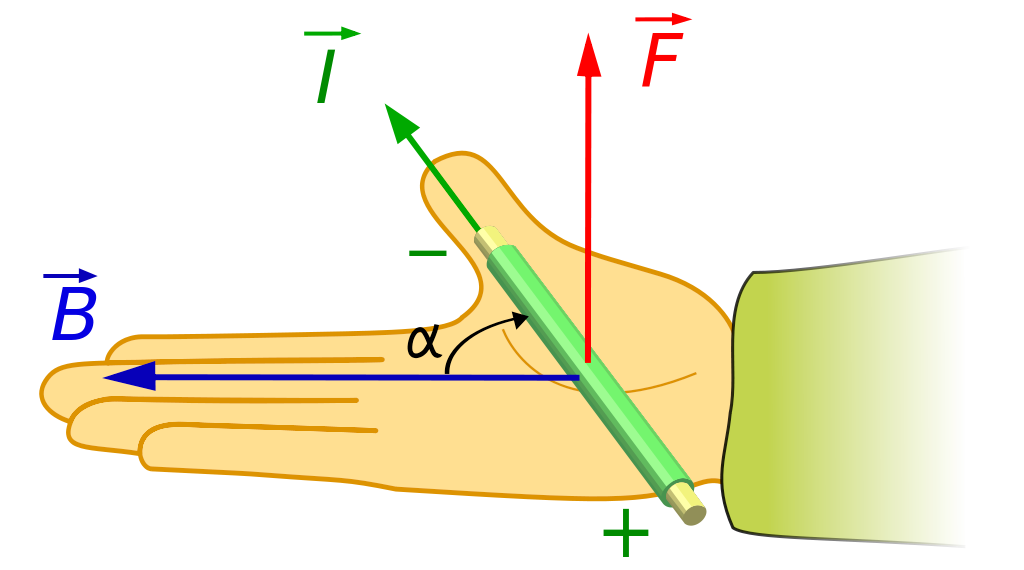
Na sua concepção, se a força atuasse nas cargas, a resistência do fio deveria variar porque afetaria a trajetória e velocidade dos Elétrons. Contudo, ele não conseguiu medir nenhuma variação na resistência.
Por isso, ele imaginou que deveria haver outro fenômeno eletromagnético anulando o efeito do campo magnético no fluxo de cargas, e o campo elétrico poderia ser esse fenômeno.
Hall montou uma experiência, conseguiu medir uma tensão – Ey, perpendicular à corrente e ao campo magnético, que surgia quando se aplicava um campo magnético no condutor3 – Figura 2.
Este fenômeno se tornou conhecido como Efeito Hall.
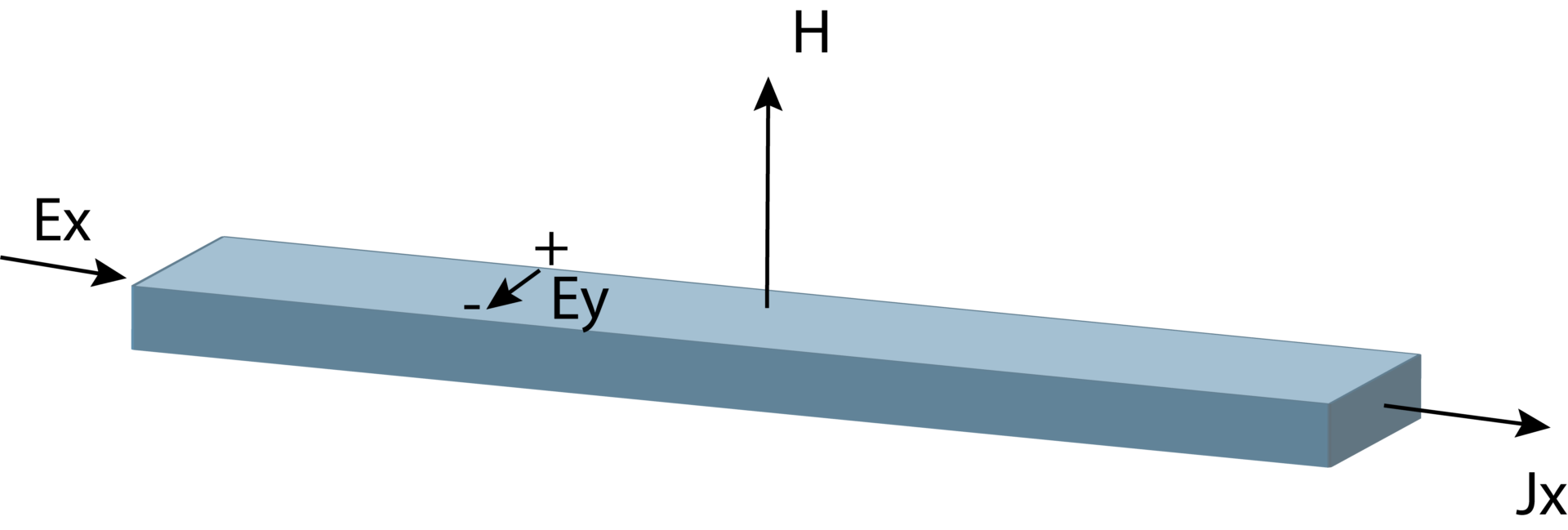
O campo elétrico Ex produz uma corrente Jx, mas o campo magnético provoca o deslocamento de cargas na direção y, que se acumulam na extremidade do condutor.
Por sua vez, este acúmulo de cargas produz um campo elétrico que repele o movimento de novos elétrons produzidos pelo campo magnético.
Desta maneira, a tensão Ey produz uma força eletrostática que se opõe à força magnética, deixando o fluxo de corrente Jx inalterado e, consequentemente, a resistência na direção x.
A Equação 1 mostra as forças nos elétrons produzida pelo campo magnético e pelo campo elétrico resultante do acumulo de cargas nas extremidades do material no eixo y.
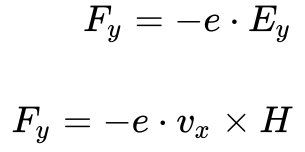
Onde:
-
- e é a carga do Elétron;
- vx é a velocidade do Elétron no eixo x .
Essas forças devem se igualar em condições de equilíbrio e a velocidade Vx é a velocidade de deriva -Vd – definida no Capítulo Condutividade e Resistividade I a partir da teoria de Drude, apesar dessa teoria ter sido posterior à descoberta de Hall.
Igualando as duas expressões da Equação 1, obtém-se o campo Ey da seguinte maneira:
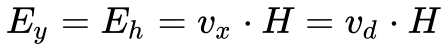
O define-se o Coeficiente de Hall – Rh – como a relação entre o campo Ey e o campo magnético – H – e a densidade de corrente, conforme mostra a Equação 3.
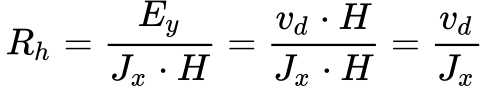
Contudo, de acordo com a Equação 4 de Condutividade e Resistividade I, a corrente Jx vale:
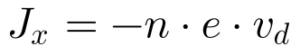
Portanto, de acordo com a Equação 5, o coeficiente de Hall depende apenas da densidade de cargas -n, da carga elétrica e da sua polaridade, e quanto maior a densidade de cargas menor o coeficiente de Hall. Por isso, o Efeito Hall se tornou um importante sistema para se medir a concentração de cargas.
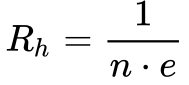
Onde:
-
- Rh é o coeficiente de Hall [m3/C ou Ω.cm/G];
- n é a densidade de cargas elétricas [elementos/m3];
- e é carga elétrica elementar [C].
Observa-se que no caso dos Elétrons, que possuem carga negativa, o valor do coeficiente de Hall se torna negativo. Porém, no caso de corrente com cargas positivas este coeficiente se torna positivo.
Este resultado se tornou extremamente importante porque permite determinar a polaridade da carga da corrente e a densidade de cargas no material.
Além disso, este fenômeno se torna mais fácil de ser observado em semicondutores do que em condutores porque o Coeficiente de Hall diminui com o aumento da densidade de cargas.
Considerando a Equação 2 de Condutividade e Resistividade I, pode-se escrever a densidade de cargas, de acordo com o modelo de Drude, como:
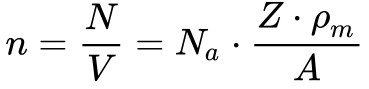
Onde:
-
- n é a densidade de Elétrons Livres [elementos/cm3];
- N é o número total de Elétrons Livres [elementos];
- V é o volume total do material [cm3];
- Na é a constante de Avogadro [elementos/mol];
- Z é número de Elétrons de Valência [elementos];
- ρm é a densidade do material [g/cm3];
- A é a massa atômica do material [g/mol].
Substituindo a Equação 6 na Equação 5, obtemos o coeficiente de Hall em função dos parâmetros do material.
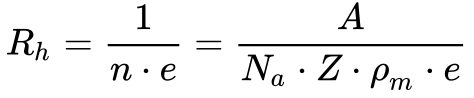
A partir da Equação 7, observa-se que o coeficiente de Hall depende da massa atômica, do número de Elétrons de Valência e da densidade do material.
A Tabela 1 apresenta os valores medidos do coeficiente de Hall para diversas substâncias no sistema CGS. 4
Como a teoria de Drude atribui exclusivamente aos Elétrons a condução de corrente, o Coeficiente de Hall deveria ser sempre negativo.
Supreendentemente, para alguns metais o coeficiente de Hall apresentou valores positivos, o que contraria a teoria de Drude de que apenas Elétrons conduzem eletricidade nos metais.
Além disso, dois elementos químicos apresentaram valores extremamente elevados, o Telúrio com valor positivo e o Bismuto com valor negativo.
Isto significa que a teoria da condução de corrente elétrica necessita de refinamentos.
Tabela - Coeficiente Hall
| wdt_ID | Material | Rh |
|---|---|---|
| 1 | Telúrio | 400 a 800 |
| 2 | Antimonio | 0,9 a 0,22 |
| 3 | Aço | 0,012 a 0,033 |
| 4 | Liga Heusler | 0,010 a 0,026 |
| 5 | Ferro | 0,007 a 0,011 |
| 6 | Cobalto | 0,0016 a 0,0046 |
| 7 | Zinco | - |
| 8 | Cadmio | 0,00055 |
| 9 | Iridio | 0,00040 |
| 10 | Chumbo | 0,00009 |
| 11 | Estanho | -0,00003 |
| 12 | Platina | -0,0002 |
| 13 | Cobre | -0,00052 |
| 14 | Prata Alemã | -0,00054 |
| 15 | Ouro | -0,00057 a 00071 |
| 16 | Constantan | -0,0009 |
| 17 | Manganes | -0,00093 |
| 18 | Paladio | -0,0007 a 0,0012 |
| 19 | Prata | -0,0008 a 0,0015 |
| 20 | Sódio | -0,0023 |
| 21 | Magnésio | -0,00094 a 0,0035 |
| 22 | Aluminio | -0,00036 a 0,0037 |
| 23 | Niquel | -0,0045 a 0,024 |
| 24 | Carbono | -0.017 |
| 25 | Bismuto | -16 |
| 26 | Fonte: Forsythe | Valores no sistema CGS |
Exercício Proposto
Converta os valores do coeficiente de Hall da Tabela 1 para o sistema SI e compare com os valores obtidos a partir da Equação 7. 5
A teoria dos Elétrons Livres funciona para diversas propriedades físicas dos materiais, tais como capacidade térmica, a condutividade térmica e a condutividade elétrica.
Contudo, ela falha na distinção entre metais, semimetais, semicondutores e isolantes.
Além disso, segundo Ashcroft, a teoria dos Elétrons Livres falha na explicação dos seguintes fenômenos:
-
- os Coeficientes de Hall positivos;
- a variação dos coeficientes de Hall com a temperatura e intensidade do campo magnético;
- a Magnetoresistência, que consiste na variação da resistência elétrica de um fio perpendicular ao campo magnético;
- os sinais da tensão do Efeito Termoelétrico e do coeficiente de Hall;
- A lei de Wiedemaan-Franz, que se baseia na teoria dos elétrons livres, falha para temperaturas entre as criogênicas e a ambiente;
- A dependência da resistividade elétrica com a temperatura;
- A dependência da resistividade elétrica coma direção (anisotropia);
Referências
- ASHCROFT N. W., Mermin, N. D., Solid State Physics, Harcourt,1976.
- FORSYTHE, W. E., Smithsonian Physical Tables, 9 ed., Knovel.
- HALL, E.H., On a New Action of the Magnet on Electric Currents, American Journal of Mathematics, vol 2, 1879, pg. 287-292. 6
- HONEYWELL SENSING AND CONTROL, Hall Effect Sensing and Application, https://sensing.honeywell.com/7
- KITTEL, C., Introduction to Solid State Physics, 8 ed., Wiley, 2005.
- RAMSDEN, E., Hall-Effect Sensors; Theory and Application, Elsevier, 2006. 8
- SOLYMAR, L., WALSH, D., SYMS, R.R.A., Electrical Properties of Materials, 10 ed., Oxford, 2019.
