“Lei de Byrne: Em qualquer circuito elétrico, os equipamentos e a fiação queimarão primeiro do que os fusíveis.”
Robert Byrne
Fusíveis se encontram em equipamentos elétricos, instalações industriais, instalações residenciais, e em sistemas de distribuição para proteção contra curtos-circuitos e sobrecorrentes elétricas. Por isso, são os dispositivos elétricos mais conhecidos e populares pelo público em geral.
O aumento anormal da corrente elétrica em equipamentos eletroeletrônicos pode provocar o derretimento do condutor e incêndios catastróficos.
Além disso, descargas atmosféricas produzem elevadas correntes induzidas em linhas de transmissão, linhas telefônicas e instalações elétricas.
Esses dispositivos, simples e baratos, possuem funcionamento complexo que envolve aspectos elétricos, mecânicos e térmicos.
Os fusíveis consistem basicamente em pequenos pedaços de material condutor de eletricidade dimensionados para suportar até determinada corrente e fundir sempre que esse valor for ultrapassado.
Eles são projetados para interromper rapidamente correntes elevadas, minimizando a energia dissipada e, consequentemente, os riscos de incêndio e outros danos.
Essas características resultaram em dispositivos pequenos e baratos. Porém, a sua destruição ao funcionar requer a manutenção de estoque para que o sistema volte a funcionar rapidamente. Esse inconveniente resultou no desenvolvimento de disjuntores, que são mais caros e volumosos.
História dos Fusíveis
Conforme visto nas experiências Temperatura e a Resistência Elétrica, Efeitos Termomecânicos da Corrente, e Fusíveis, a corrente elétrica nos condutores metálicos produz aquecimento e a resistividade desses materiais aumenta com a temperatura.
Em 1883, William Henry Preece publicou o primeiro trabalho que relaciona a corrente de fusão de um condutor metálico com seu diâmetro.
Preece, ex-aluno de Faraday, se tornou engenheiro-chefe dos correios Britânicos e a rede de telégrafos com fio se mostrou muito sensível às descargas atmosféricas.
Portanto, ele se envolveu com o problema de proteger a rede de telégrafos contra sobrecorrentes.
Diversos dispositivos de proteção surgiram, mas todos esbarravam na questão de qual a corrente máxima suportável.
Estes dispositivos deveriam suportar as correntes normais dos telégrafos, mas precisam fundir com as sobrecorrentes. Nascia a ideia do fusível. 1
Preece realizou diversas experiências com fios de diversos materiais, diâmetros e comprimentos.
Além disso, os condutores estavam livres no espaço de tal forma que não houvesse impedimentos para a transferência de calor.
Primeiramente, ele constatou que, descontado o efeito de resfriamento dos terminais2, a corrente de fusão permanecia a mesma independentemente do comprimento dos fios.

A independência do comprimento contraria o senso comum, mas se mostrou teoricamente correta. Porém, a corrente de fusão dependia do diâmetro e do material.
Além disso, Preece observou que o ponto de ocorrência da fusão variava, e atribuiu este comportamento a irregularidades nos fios.
Inicialmente, ele utilizou fios de Platina, Cobre, Prata e Ferro de diversos diâmetros, mas todos com o mesmo comprimento.
Analisando os dados medidos, Preece constatou que a Equação 1 fornecia a corrente de fusão do fio, e a constante a dependia do material.
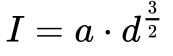
Onde:
-
- I é a corrente [A];
- a é a constante de Preece [A/mm3/2];
- d é o diâmetro do fio [mm].
Análise Teórica

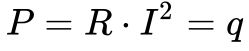
Onde:
-
- P é a potência elétrica dissipada no fio [W];
- R é a resistência elétrica do fio [Ω};
- I é a corrente elétrica no fio [A];
- q é o calor dissipado pelo fio para o meio ambiente [W];
A Equação 3 mostra que o calor transferido do fio para o ar (q) depende do diâmetro do fio (d), do comprimento do fio (L), e da densidade de energia dissipada (h).
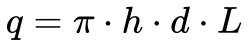
Onde:
-
- q é a potência dissipada pelo fio [W];
- h é fluxo de calor dissipado por área do fio [W/m2];
- d é o diâmetro do fio [m];
- L é o comprimento do fio [m].
Como a descoberta de Peerce ocorreu 7 anos antes dos resultados de Drude, ele não relacionou sua constante com a resistividade, apesar de identificar sua relação com as dimensões e tipos de materiais.
Considerando a resistividade elétrica do fio, a Equação 4 fornece o valor da resistência em função das dimensões do fio.
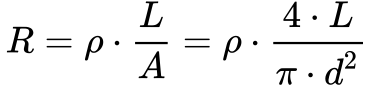
Onde:
-
- R é a resistência elétrica do fio[Ω];
- ρ é a resistividade elétrica do fio [Ω.m];
- L é o comprimento do fio[m];
- A é a área da seção reta do fio[m2].
- d é o diâmetro do fio [m]
Substituindo as Equações 3 e 4 na Equação 2, obtém-se que:
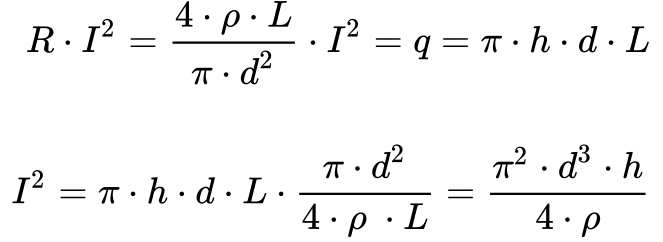
Observa-se que a Equação 5 permite determinar a constante de Peerce da seguinte maneira:
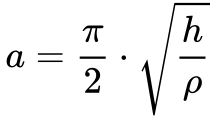
A Equação 6 mostra que a constante de Peerce depende da resistividade elétrica do material e do fluxo de calor dissipado pela área superficial do fio.
A resistividade elétrica já foi devidamente analisada no capítulo de Condutividade e Resistividade I, mas a densidade de calor dissipado requer algumas considerações.
Supondo que a transferência de calor do fio para o meio ambiente ocorra apenas por Radiação Térmica, pode-se aplicar a Lei de Stefan-Boltzmann. 3
A partir da Lei de Stefan-Boltzmann, a Equação 7 fornece o fluxo de calor no fio.
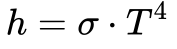
Onde:
-
- h é fluxo de calor dissipado por área do fio [W/m2 ];
- σ é a constante de Stefan-Boltzmann [5,670 373 e-8 W/(m2 K4)];
- T é a temperatura de equilíbrio do fio [K]
Substituindo a Equação 7 na Equação 6, obtemos a seguinte expressão:
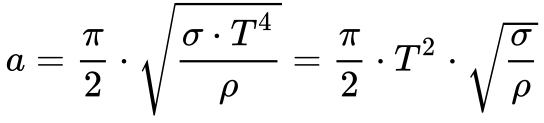
Onde:
-
- a é a constante de Peerce [A.m -3/2];
- T é a temperatura no fio [K];
- σ é a constante de Stefan-Boltzmann [ 5,670 373 e-8 W/(m2 K4)];
- ρ é a resistividade elétrica do fio [Ω.m];
Observa-se que a constante de Preece varia com o quadrado da temperatura do fio e, conforme visto anteriormente, a resistividade elétrica dos materiais também depende da temperatura.
Contudo, as temperaturas notáveis; temperatura de fusão, temperatura de ebulição e ponto de Drapper, apresentam valores bem definidos.
Por isso, Preece determinou seu coeficiente para a temperatura de fusão dos materiais porque os fios sempre rompem nessa temperatura.
A Tabela abaixo apresenta o coeficiente de Preece de diversos metais utilizados como condutores na engenharia elétrica.
A liga de Estanho e Chumbo, muito utilizada para soldar componentes eletrônicos e funcionar como fusível, apresenta dados pouco precisos porque as propriedades das ligas dependem do percentual de sua composição de cada elemento que as constitui.
Coeficiente de Preece
| wdt_ID | Material | Coeficiente de Preece(A/cm^3/2) | Temperatura de Fusão (C) | Condutividade Elétrica (MS/m) |
|---|---|---|---|---|
| 1 | Cobre | 2,531 | 1.084,62 | 59,0 |
| 2 | Alumínio | 1,874 | 660,32 | 38,0 |
| 3 | Platina | 1,278 | 1.768,30 | 9,4 |
| 4 | Prata | 1,292 | 961,78 | 62,0 |
| 5 | Ferro | 0,778 | 1.538,00 | 10,0 |
| 6 | Estanho | 0,406 | 231,93 | 9,1 |
| 7 | Estanho/Chumbo (solda) | 0,326 | 183,00 | 5,0 |
| 8 | Chumbo | 0,341 | 327,46 | 4,8 |
Fontes: Ness Engineering Inc , Propiedades da Solda e Tabela Periódica
Referências
- CHEN, K. C.; WARNE, K. L.; LIN, Y. T.; et al. Conductor fusing and gapping for bond wires, Progress In Electromagnetics Research M, vol.31,199-214,2013.
- JOHNS, A.T., WARNE, D.F., Electric Fuses, IET, 2008.
- PREECE, W. H., On the heating effects of electric currents, Proc. R. Soc. Lond, 36, p. 464-471, publicado em 1 jan. 1883.
- PREECE, W. H., On the heating effects of electric currents II, Proc. R. Soc. Lond, 43, p. 280-295, publicado em 1 janeiro 1887.
