“O ferro, próximo de uma espiral de fio de cobre conduzindo uma corrente elétrica, torna-se magnético e, a seguir, atrai outras peças de ferro ou um ímã de aço adequadamente colocado.”
Introdução
O magnetismo existe em decorrência do movimento de cargas elétricas e, como cargas elétricas (Elétrons e Prótons) formam a matéria, o magnetismo afeta a matéria e a matéria afeta o magnetismo.
Mas como matéria e magnetismo se relacionam?
Os Elétrons, que envolvem os átomos, formam uma armadura de cargas elétricas em movimento. Consequentemente, os Elétrons afetam e são afetados pelo magnetismo. Nucleons1 se encontram mais isolados no núcleo e, por serem mais pesados, movem-se mais lentamente. Por isso, os nucleons influenciam menos as propriedades magnéticas dos materiais.
Neutrons, eletricamente neutros, deveriam apresentar insensibilidade ao campo magnético. Contudo, como os Nucleons são formados por partículas subatômicas2, que possuem carga elétrica, massa, e spin distintos, o magnetismo os afeta e possibilitou o desenvolvimento de equipamentos de ressonância magnética.
Porém, antes de iniciarmos o estudo dos materiais magnéticos convém rever alguns conceitos de Eletromagnetismo.
Sistemas de Unidades
Existem três sistemas de unidades magnéticas utilizados no mundo, o Sistema CGS ou Gaussiano e dois que utilizam o Sistema Internacional (SI) baseado no sistema MKSA, que se tornou padrão mundial no comércio e na engenharia. Os dois sistemas que utilizam o Sistema SI denominam-se de Kennelly e Sommerfeld.
Contudo, cientistas ainda utilizam o sistema CGS e diversos livros importantes sobre materiais utilizam este sistema. Por isso, torna-se necessário conhecer as diferenças entre os sistemas para compreendermos os diferentes textos.
O Sistema CGS se baseia nas grandezas Centímetro, Grama e Segundo, e se tornou o preferido na ciência dos materiais porque utiliza unidades menores do que o sistema MKS, que utiliza o Metro, Kilo e Segundo.
Porém, a conversão de unidades magnéticas apresenta algumas dificuldades adicionais porque as constantes eletromagnéticas foram definidas diferentemente nos dois sistemas, ao contrário de outras equações da Física.
Conforme mostrado abaixo, as Equações de Maxwell foram definidas de forma distinta nos dois sistemas de unidades.

As equações no sistema SI parecem mais simples porque não apresentam constantes multiplicativas.
Contudo, a simplicidade se altera quando consideramos as relações constitutivas, conforme mostra a Equação 2.
No sistema CGS, as equações ficam mais elegantes porque existe apenas uma constante: a velocidade da luz. Por isso, os físicos continuam utilizando o sistema CGS.

Nas relações constitutivas surgem dois novos elementos que caracterizam o efeito dos campos elétrico e magnético nos materiais, denominados de vetor de Magnetização – M – e vetor Deslocamento – D.
A única diferença entre os sistemas de Sommerfeld e Kenelly reside na relação constitutiva do campo magnético.
Sommerfeld considera a permeabilidade do vácuo multiplicando o vetor Intensidade do Campo Magnético – H – e o vetor Magnetização – M, enquanto Kennelly considera a permeabilidade do vácuo multiplicando apenas o vetor Intensidade do Campo Magnético – H, conforme mostra a Equação 3.
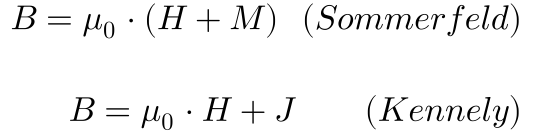
A diferença entre os dois modelos reside na definição do efeito do campo magnético nos materiais.
O vetor Magnetização – M – possui a mesma unidade [A/m] do Vetor Intensidade de Campo Magnético – H no modelo de Sommerfeld. Como o vetor H se encontra associado à corrente geradora do campo magnético, o vetor M se relaciona com o Momento Magnético líquido existente no material produzido por todas os componentes dos átomos.
Por outro lado, no Modelo Kennelly o vetor de Polarização Magnética – J – possui a mesma unidade do vetor Densidade de Fluxo Magnético – B, que possui a unidade de Tesla (T) no sistema SI, e Wb.m e emu no sistema CGS.
Neste curso, utilizaremos o sistema SI com a convenção de Sommerfeld, mas saber da existência dessas diferenças torna-se importante para compreender diversos outros livros e artigos sobre este assunto.
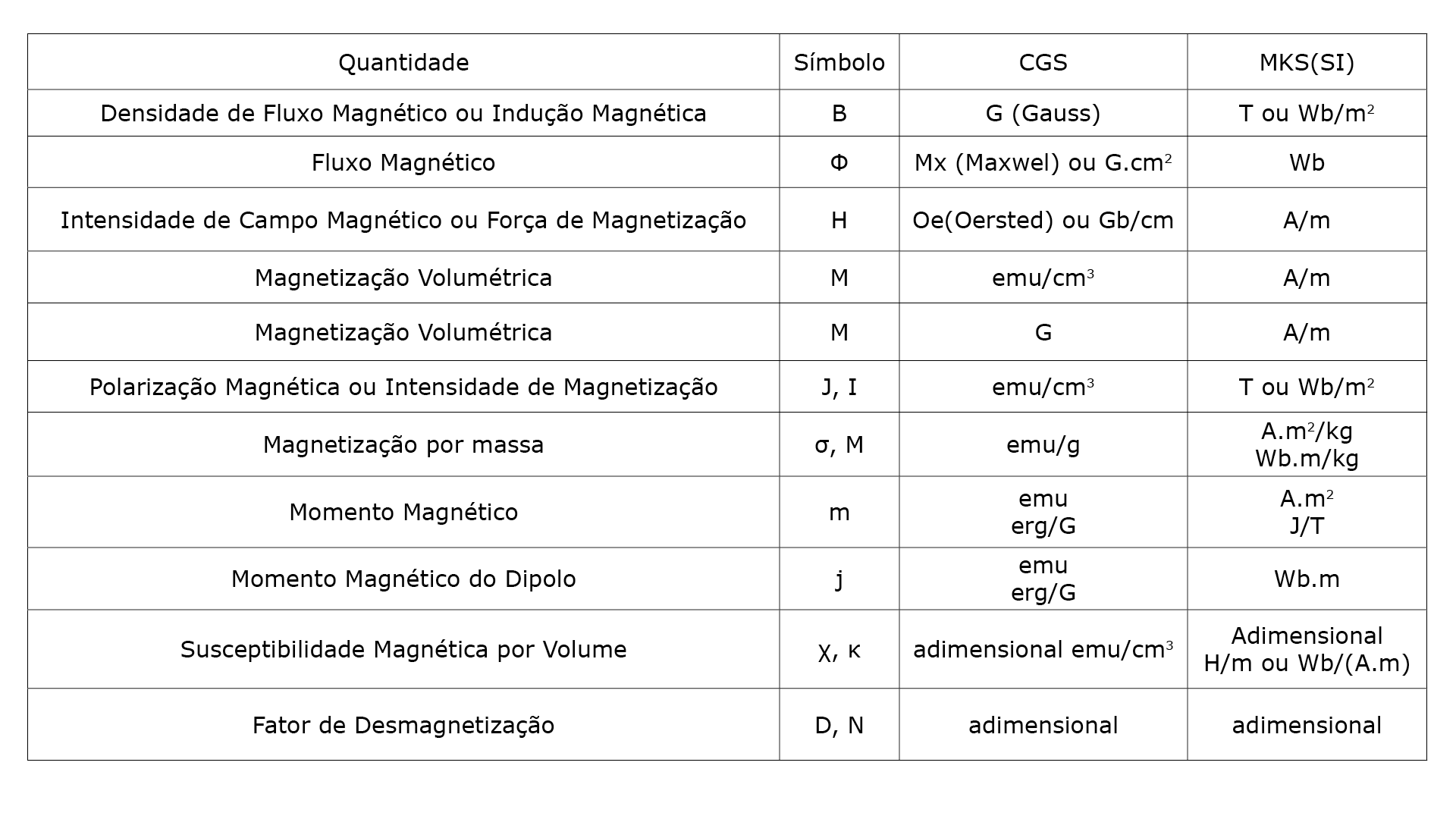
A Tabela 1 apresenta as principais grandezas magnéticas nos sistemas SI e CGS com seus respectivos símbolos e unidades.
Dipolo Magnético
O Dipolo Magnético consiste no elemento fundamental do magnetismo, e pode-se representá-lo de duas maneiras.
A primeira consiste em dois polos magnéticos situados bem próximos, e a segunda através de um pequeno anel de corrente elétrica.
A Figura 1 mostra o modelo de dois polos magnéticos, e a Figura 2 o modelo do anel de corrente.
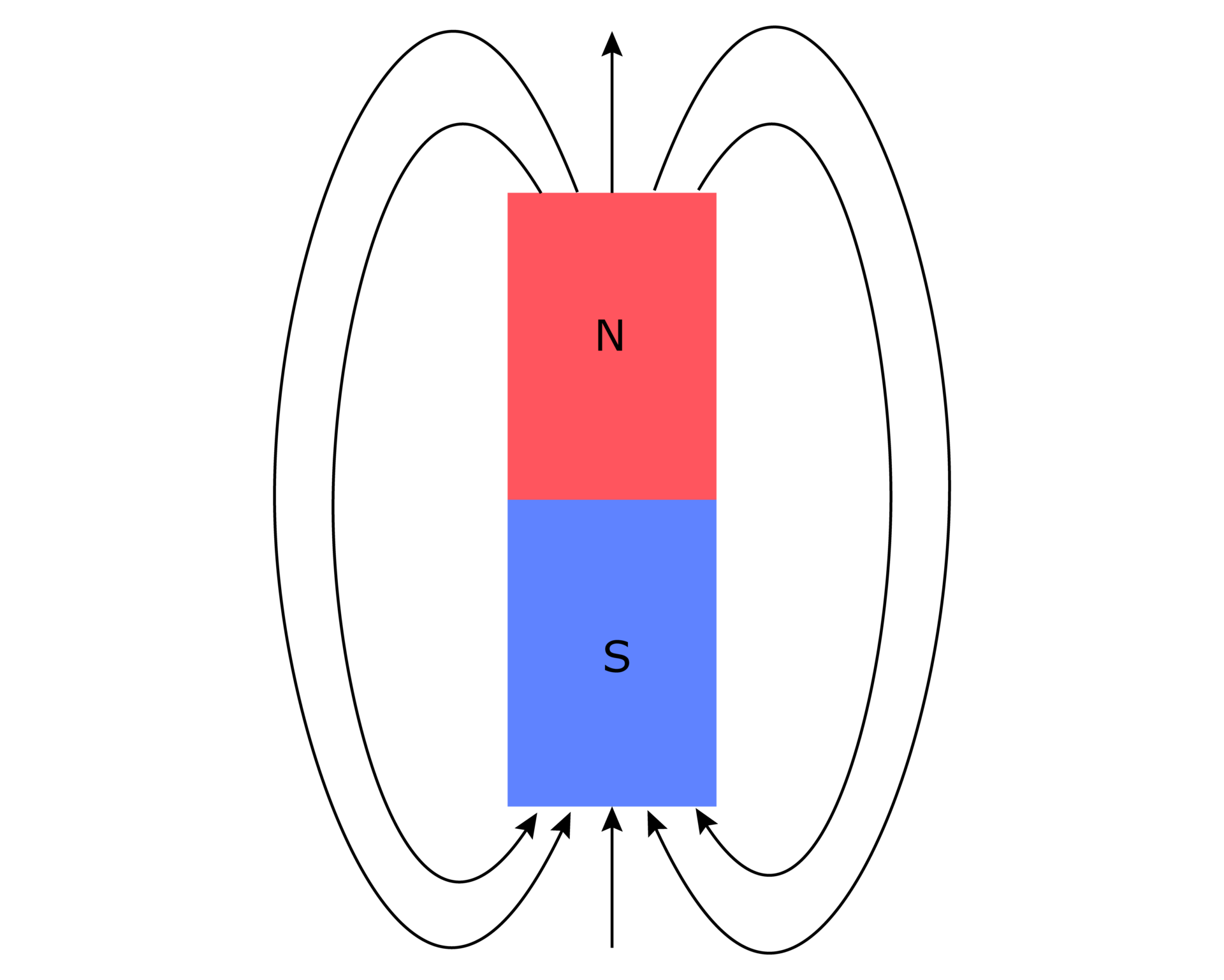
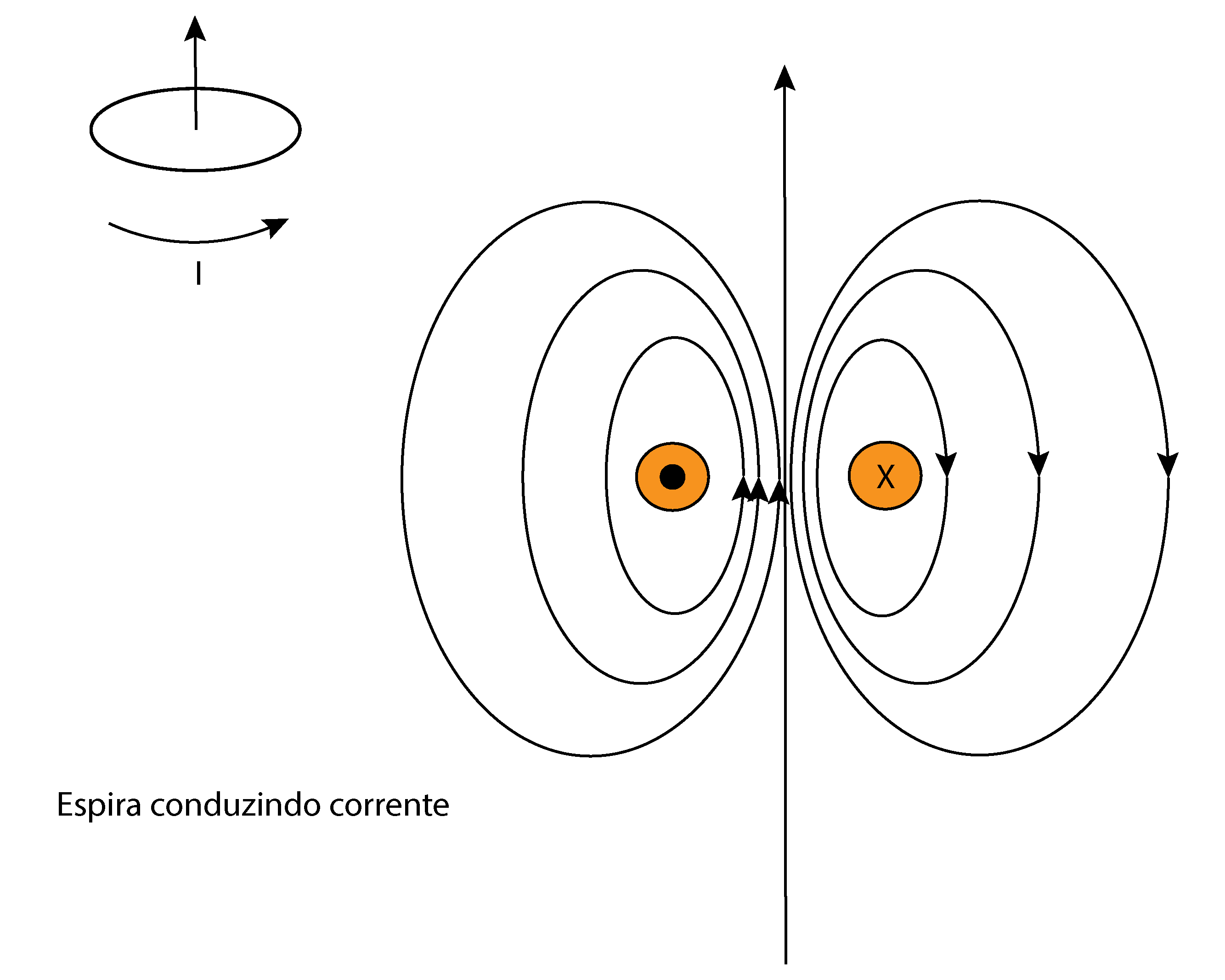
O modelo que utiliza a corrente elétrica torna-se muito conveniente para explicar o magnetismo orbital dos elétrons e, com algum esforço de imaginação, no magnetismo gerado pelo spin das partículas que possuem carga elétrica.
A Equação 4 fornece o momento angular de um Elétron se movimentando numa órbita circular de raio r com velocidade linear v.
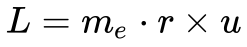
Onde:
-
- L é o momento angular;
- me é a massa o Elétron;
- r é o raio da órbita;
- u é a velocidade linear do Elétron.
O produto vetorial do raio pela velocidade determina que o vetor momento angular possui uma direção perpendicular ao plano r x u orientado de acordo com a regra da mão direita, conforme mostra a Figura 2.
Os Elétrons orbitando o núcleo dos átomos criam uma corrente elétrica definida pela carga do Elétron [C] dividida pelo tempo [s] gasto para orbitar o núcleo.
Este tempo depende da velocidade linear do Elétron e do raio da sua órbita de acordo com a Equação 5.
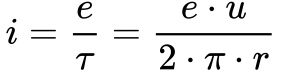
Onde:
-
- i é a corrente;
- e é a carga do Elétron;
- u é a velocidade linear do Elétron;
- r é o raio da órbita.
Finalmente, define-se o momento magnético produzido por uma corrente da seguinte maneira:
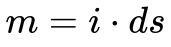
Onde:
-
- m é o momento magnético [A.m2];
- i é a corrente [A];
- ds é o vetor da área percorrida pela corrente[m2].
Aplicando essas expressões ao Elétron em sua órbita circular, obtem-se a seguinte relação.
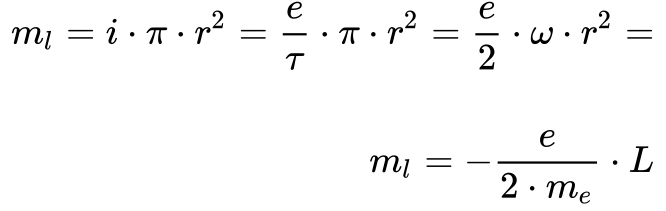
Onde:
-
- ml é o momento magnético orbital do Elétron;
- e é a carga do Elétron;
- me é a massa do Elétron;
- L é o momento angular do Elétron.
Observa-se, a partir da Equação 7, que o momento magnético orbital possui sinal inverso ao do momento angular devido ao sinal da carga do Elétron.
O momento magnético reage à presença de campo magnético externo adquirindo energia e torque de acordo com as expressões abaixo:
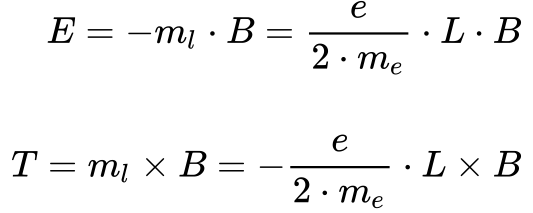
Onde:
-
- E é a energia adquirida pelo Elétron;
- ml é o momento magnético orbital do Elétron;
- B é a densidade de fluxo magnético;
- e é a carga do Elétron;
- me é a massa do Elétron;
- L é o momento angular do Elétron.
O torque decorrente do campo magnético externo produz um movimento de presseção no momento magnético conforme mostra a Figura 3.
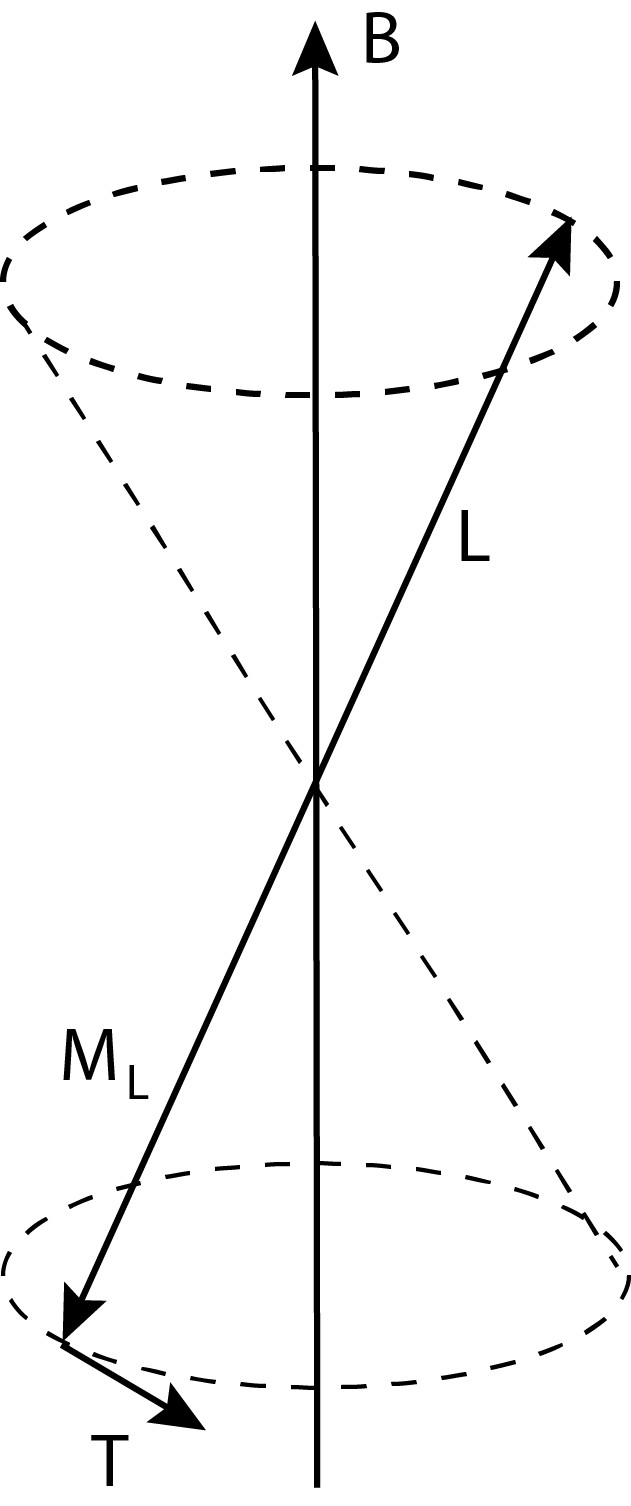
Apesar das órbitas dos Elétrons nos átomos não serem circulares, eles possuem um momento angular determinado pela Mecânica Quântica. A utilização deste modelo atômico clássico apenas facilita o entendimento dos conceitos.
Na verdade, a Equação de Schröndiger determinou quatro números quânticos que caracterizam as órbitas dos Elétrons nos átomos, sendo o momento magnético e o spin responsáveis pelo comportamento magnético dos materiais.
Exemplo – Como traçar as linhas de Campo Magnético?
Na presença de campo magnético externo, o momento magnético dos elétrons e seu spin afetam o campo magnético no interior do material.
Como a determinação do comportamento individual das cargas elétricas no interior dos materiais se torna extremamente complexa, a engenharia trata os fenômenos magnéticos no interior dos materiais de forma macroscópica.
Por isso, define-se o vetor de Magnetização – M- como o efeito resultante de todos os momentos magnéticos das cargas existentes no interior dos materiais. Em função disso, o vetor de Magnetização depende do vetor densidade de fluxo magnético -B.
A Figura 4 apresenta um circuito magnético composto por duas bobinas enroladas ao redor de um material com permeabilidade magnética μ.
Onde:
-
- H é a intensidade do campo magnético [A.m]
- I é a corrente elétrica [A]
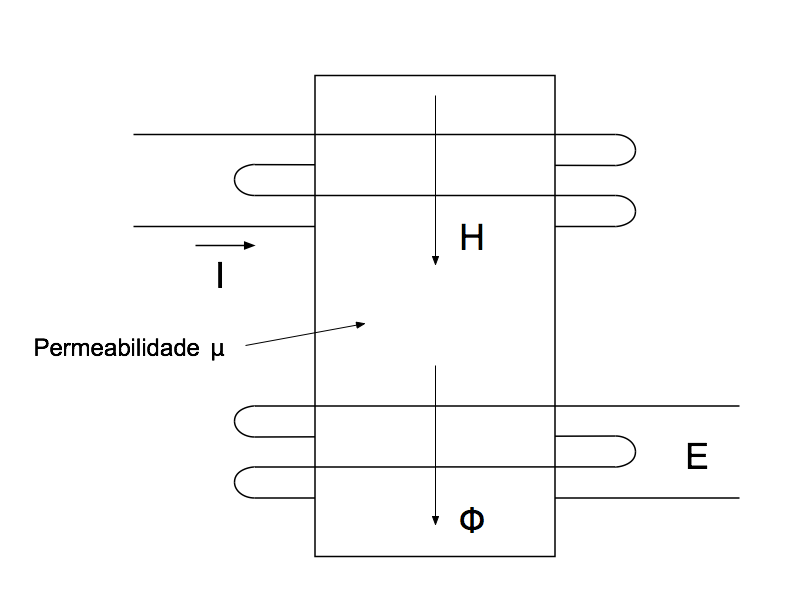
A corrente no enrolamento superior -I- produz um campo magnético H orientado verticalmente para baixo de acordo com a regra da mão direita.
Por sua vez, este campo magnético produz um fluxo magnético no material – Φ, cuja densidade -B- é dada por:
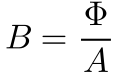
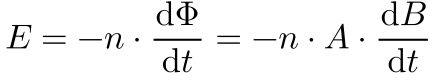
Portanto, o campo magnético H depende corrente no primeiro enrolamento e a densidade de fluxo magnético B e a sua variação no tempo produz uma tensão no segundo enrolamento. 3
A Densidade do Fluxo Magnético -B- relaciona-se com o Campo Magnético -H- através da Permeabilidade Magnética -μ- do material conforme a equação 3.
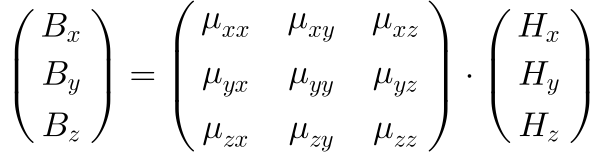
Onde:
-
- B é a densidade de fluxo magnético, ou campo magnético, ou indução magnética [Wb/m2].
- H é o vetor campo magnético ou intensidade do campo magnético [A/m].
- μ é o tensor permeabilidade magnética [H/m].
Como B e H são vetores tridimensionais, a Permeabilidade Magnética se torna um tensor de segunda ordem. 4
Em materiais magnéticos lineares e isotrópicos, a permeabilidade magnética pode ser escrita da seguinte maneira:
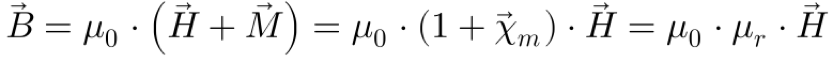
Onde:
-
- M é o vetor magnetização [A/m]
- μ0 é a permeabilidade do vácuo [4π .10-7 H/m]
- μr é a permeabilidade relativa do material.
- χm é a susceptibilidade magnética do material.
A análise da permeabilidade magnética dos materiais permiti agrupá-los em três categorias:
-
- Diamagnéticos;
- Paramagnéticos;
- Ferromagnéticos;
A Figura 2 apresenta a permeabilidade magnética destas categorias em comparação com a permeabilidade do vácuo. Observa-se que:
-
- a permeabilidade de materiais diamagnéticos – μd– é inferior à permeabilidade do vácuo;
- a permeabilidade dos paramagnéticos é superior;
- e a dos ferromagnéticos é muito maior, mas satura para valores elevados de densidade de campo magnético.
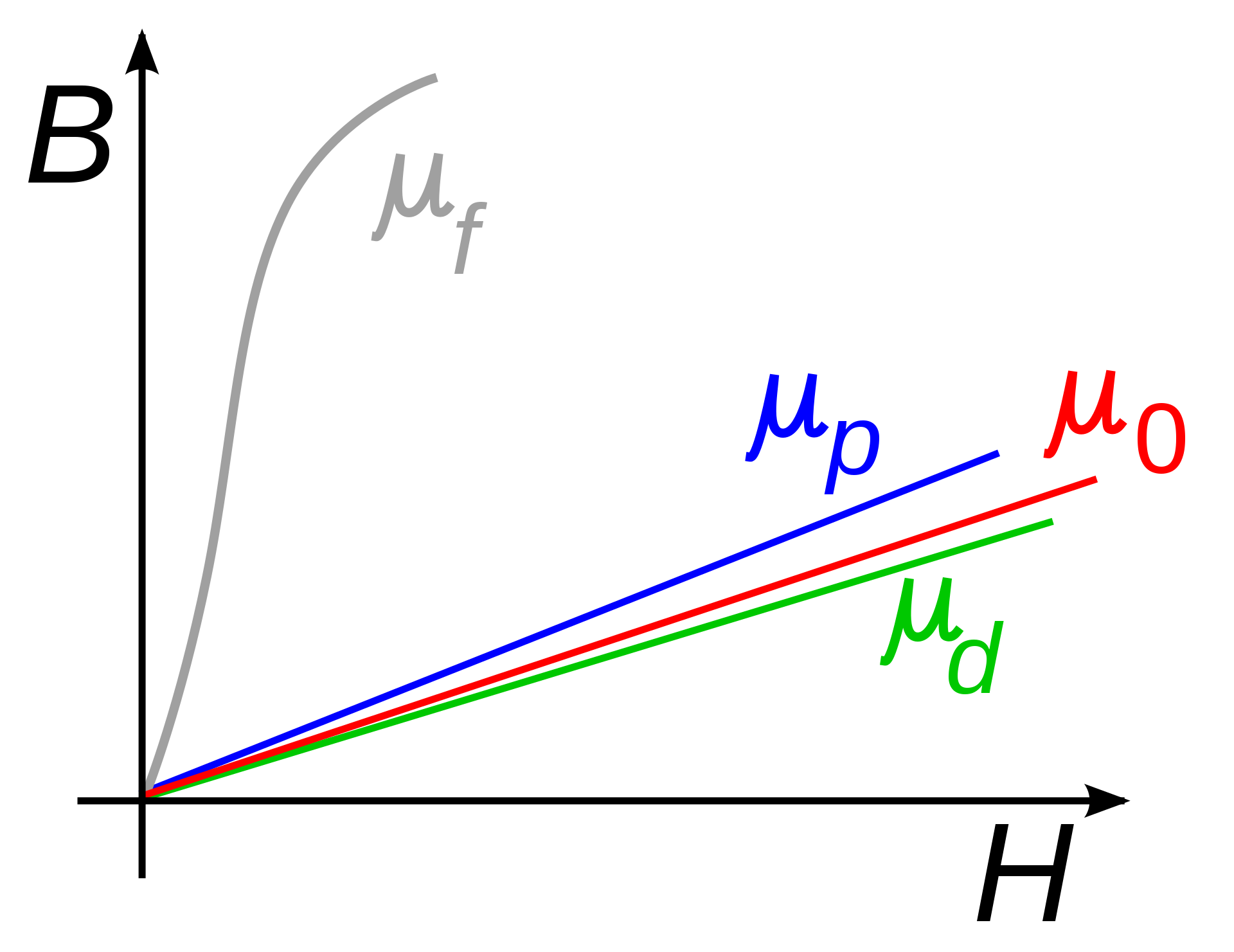
Fonte: Zureck
Este link apresenta a Tabela Periódica Magnética dos elementos.
Susceptibilidade Magnética
A Susceptibilidade Magnética consiste na propriedade magnética que caracteriza os diversos tipos de materiais magnéticos.
As Propriedades Magnéticas dos materiais são:
-
- Susceptibilidade Magnética;
- Permeabilidade Magnética;
- Retentividade;
- Histerese;
- Saturação Magnética;
- Remanência Magnética;
- Coercividade Magnética;
- Permeabilidade Diferencial;
- Temperatura Curie;
- Piromagnetismo;
- Magnetoeletricidade;
- Piezeomagnetismo.
Referências
- JILES, D. Introduction to Magnetism and Magnetic Materials. Springer. 1991.
- FURLANI, E. P. Permanent Magnet and Electromechanical Devices. Academic Press. 20015
- TUMANSKI, S. Handbook of Magnetic Measurements. CRC. 2011. 6
- SPALDIN, A.S., Magnetic Material – Fundamentals and Applications, Cambrige, 2 ed., 2011. 7
