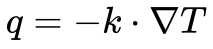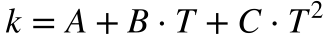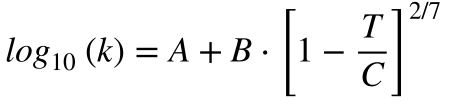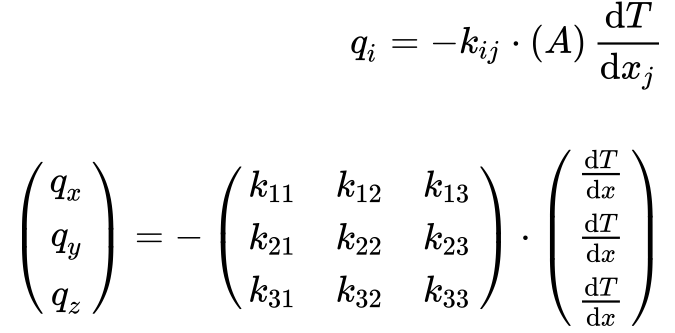Condutividade Térmica

“Se você não suporta o calor, saia da cozinha”

Harry Truman

A condutividade térmica consiste na propriedade dos materiais sólidos em conduzir calor e se encontra intimamente relacionada com a condutividade elétrica.

O fluxo de calor, ocasionado por gradientes de temperatura nos materiais, ocorre de três maneiras; Condução, Convecção e Radiação. A forma predominante de transferência de calor depende do sistema e das diferenças (gradiente) de temperatura.

A condução consiste na forma de transferência de calor no interior dos materiais sólidos, e ocorre através da transmissão de energia entre átomos e moléculas a partir dos pontos mais quentes para os mais frios.

A lei de Fourier descreve seu comportamento de acordo com a Equação 1.

Onde:

• • q é o fluxo de calor em função do tempo por unidade de área normal ao fluxo de calor [W/m²]^;
  • k é a condutividade térmica do material [W/(m².K)];
  • ▽T é o gradiente da temperatura [K/m ou C/m];

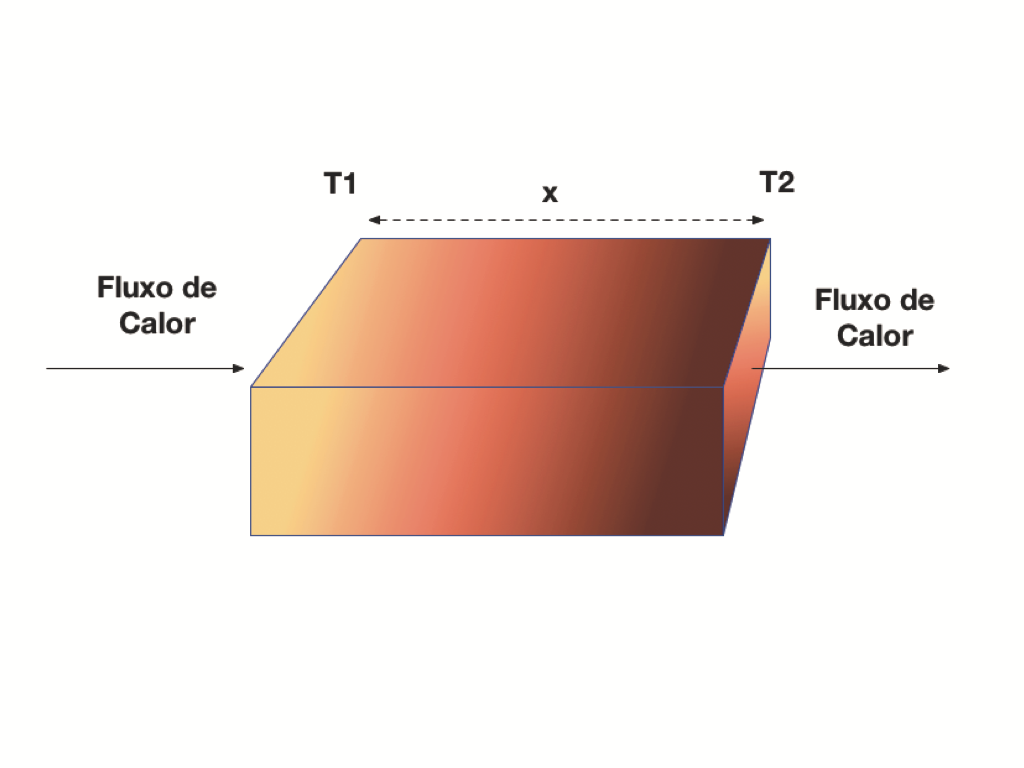
A Figura 1 mostra a condução de calor unidirecional. Neste caso, a Equação 1 transforma-se na Equação 2.

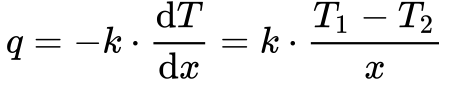
A Condutividade Térmica representa a capacidade do material conduzir calor em regime permanente. Ela depende do tipo de material, sendo mais elevada para os metais e menor para líquidos e gases.

Contudo, existem exceções.

Por exemplo, o Diamante natural tipo IIa (sem nitrogênio) apresenta condutividade térmica de 2 300 W/m/K na temperatura ambiente, e o Grafeno 5 000 W/m/K. Ambos são variações cristalinas de carbono, que não pertence ao grupo de metais.

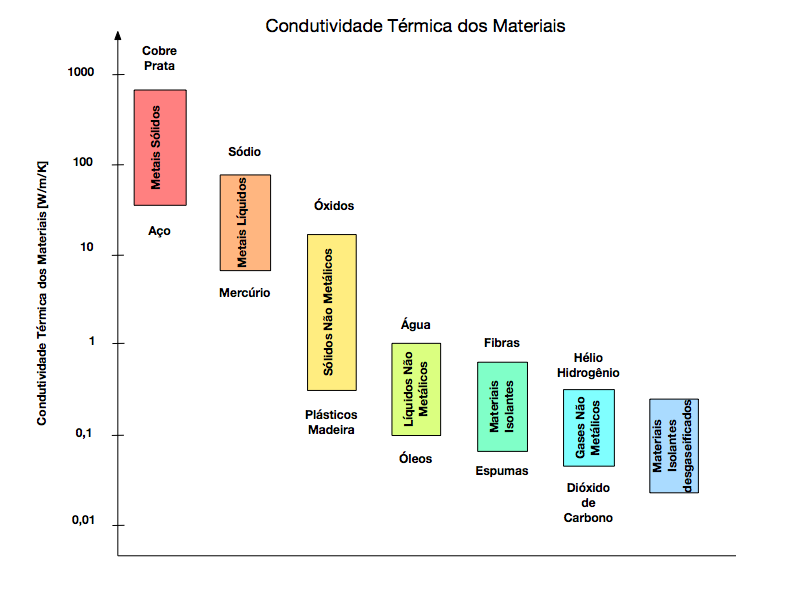
A Figura 2 apresenta a distribuição dos valores de condutividade térmica dos diversos tipos de materiais. Observa-se que os metais apresentam os valores mais elevados de condutividade térmica e os materiais isolantes desgaseificados possuem os menores valores.

Em 1853, alguns anos após a descoberta da Lei de Ohm, mas antes da Teoria de Drude sobre a condutividade elétrica, Gustav Wiedemann e Rudolph Franz descobriram empiricamente que as condutividades térmica e elétrica se encontram relacionadas da seguinte maneira:

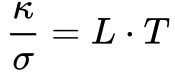
Onde:

• • κ é a condutividade térmica [W/m/K];
  • σ é a condutividade elétrica [S/m]
  • L é a constante de Lorenz [2,443 004 509 073 67 x 10^-8 W.Ω/K²]¹;
  • T é a temperatura[K].

Somente em 1872, 19 anos após a descoberta de Wiedermann e Franz e antes da Teoria de Drude, Ludvig Lorenz calculou o valor da constante, que passou a levar seu nome.

A teoria para explicar a relação entre condutividades elétrica e térmica se baseia na Teoria Cinética dos Gases e na Teoria de Drude.

De acordo com a Teoria Cinética dos Gases, a Equação 4 determina a Condutividade Térmica.

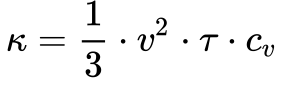
Onde:

• • κ é a condutividade térmica
  • v é a velocidade média das moléculas do gás;
  • τ é o tempo médio entre colisões das moléculas;
  • c_v é o calor específico a volume constante.

Drude aplicou a Teoria Cinética dos Gases aos Elétrons de Valência e dividindo a Equação 4 pela Equação 13 da página Condutividade Elétrica, obteve a seguinte expressão:

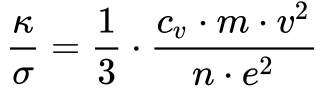
Considerando as expressões abaixo oriundas da Teoria Cinética dos Gases.

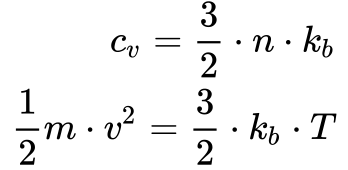
Drude aplicou a Equação 6 na Equação 5 e obteve o seguinte resultado para a Constante de Lorenz:

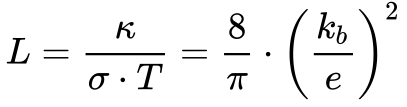
Onde:

• • kb é a constante de Boltzmann;
  • e é a carga do Elétron.

Este valor, obtido muito antes da Mecânica Quântica apresenta um pequeno erro, que foi posteriormente corrigido da seguinte maneira:

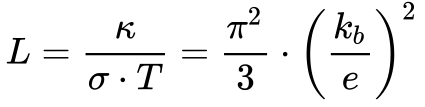
Na prática, a condutividade térmica varia com a temperatura e com a orientação de materiais anisotrópicos. De uma maneira geral, ela diminui com o aumento da temperatura para os metais e aumenta nos gases. Empiricamente, a condutividade térmica dos materiais varia com a temperatura da seguinte maneira [Yaws]:

Tabela 1. Condutividade Térmica – Inorgânicos

Nome	Fórmula	A	B	C	k @ 25 C (W/(m.K)	Tmin (K)	Tmax (K)
Prata	Ag	438,22	-2,30e-2	-354e-5	428,23	200	1200
Alumínio	Al	228,21	5,80e-2	-8,68e-5	237,79	200	934
Ouro	Au	335,45	-5,83e-2	-7,48e-6	317,42	200	1300
Cobre	Cobre	426,30	-8,39e-2	9,38e-6	402,11	200	1300
Ferro	Fe	117,32	-1,38e-1	5,42e-5	81,11	200	1000
Sal	NaCl	51,61	-2,96e-1	4,71e-4	5,157	80	380
Silício	Si	436,78	-1,29	1,11e-3	152,24	250	600
Água	H20	-0,28	4,61e-3	-5,54e-6	0,607	273	633
Chumbo	Pb	39,33	-1,35e-2	5,15e-7	35,36	200	600
Estanho	Sn	92,31	-1,15e-1	1,0e-4	66,78	200	600
Kanthal A-1	FeCrAl	10,76	1,15e-2	3,43e-6	11
Constantan	55%Cu 45%Ni				49
Tungstênio	W	192,98	-7,85e-2	1,44e-5	170,84	250	3400
Fonte: Yaws

 

A partir da Equação 3, pode-se calcular a Relação de Lorenz da seguinte maneira:

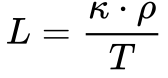
Utiliza-se a denominação de Relação de Lorenz Experimental para diferenciar da Constante de Lorenz porque a constante possui origem teórica e a Relação se origina de dados medidos.

A Tabela 2 apresenta a Relação de Lorenz para alguns materiais calculada a partir de resistividade elétrica e condutividade térmica medidas. 

Tabela 2. Relação de Lorenz Experimental

Material	Resistividade Elétrica [E-8. Ohms.m] @ 20C	Condutividade Térmica [W/(m.K)] @ 25 C	Relação de Lorenz [E-8. W.Ohm/K^2]
Alumínio	2,65	210	1,90
Chumbo	20,8	35,36	2,51
Cobre	1,678	402,11	2,303
Constantan	45,38	49	7,59
Estanho	11,5	66,78	2,62
Ferro	9,61	81,11	2,66
Kanthal A-1	145	11	5,4
Ouro	2,214	317,42	2,399
Prata	1,587	428,23	2,319
Sal	4,77	5,157	0,08
Silício	10000	152,24	5196
Tungstênio	5,28	170,84	3,08
Água	1,818 E5 [Ohm.m]	0,607	377

Fonte: Yaws Condutividade Térmica, CRC Handbook resistividade elétrica

 

A análise da Tabela 2 mostra que a Relação de Lorenz se aproxima do valor teórico apenas para os elementos metálicos. ²

O Sal, o Silício e a Água apresentam valores extremamente discrepantes porque não são metais. O Sal é um composto químico, o Silício um semicondutor e a água um isolante elétrico.

Adicionalmente, as ligas metálicas³ exibiram valores da mesma ordem de grandeza do valor teórico, mas três e duas vezes maiores respectivamente.

Finalmente, os elementos metálicos Alumínio e Tungstênio apresentaram valores 22% menor e 26% maior respectivamente do que o valor teórico.

Isto indica que os modelos teóricos da condução térmica e resistividade elétrica ainda requerem aperfeiçoamentos.

Contudo, pode-se utilizar os valores das Relações de Lorenz para obter as relações entre condutividade térmica e resistividade elétrica de um grupo importante de condutores elétricos.

A análise da Equação 9 mostra que a condutividade térmica tende para A quando a temperatura tende para o zero absoluto. Contudo, todas as expressões empíricas possuem validade apenas nos intervalos de temperatura apresentados nas tabelas.

Por outro lado, para líquidos orgânicos, a condutividade térmica varia da seguinte maneira [Yaws]:

Tabela 2. Condutividade Térmica – Orgânicos

Fórmula	Nome	A	B	C	k @ 25 C	Tmin	Tmax
CH4	Metano	-1,0976	0,5387	190,58		91	181
C2H60	Etanol	-1,3172	0,6987	516,25	0,1694	159	490
C5H402	Furfural	-1,365	0,7132	657	0,1718	237	624
Fonte: Yaws

Nem todos os materiais são isotrópicos e, no caso de materiais anisotrópicos, a condução de calor ocorre de acordo com a Equação 11.

Onde a condutividade térmica se torna um tensor polar simétrico de segunda ordem, k_ij=k_ji.

Conforme mostra a Figura 3, pode-se interpretar o fluxo de calor no processo de condução térmica como uma fonte de corrente, a temperatura como tensão elétrica, e a resistência térmica dada pela Equação 12.

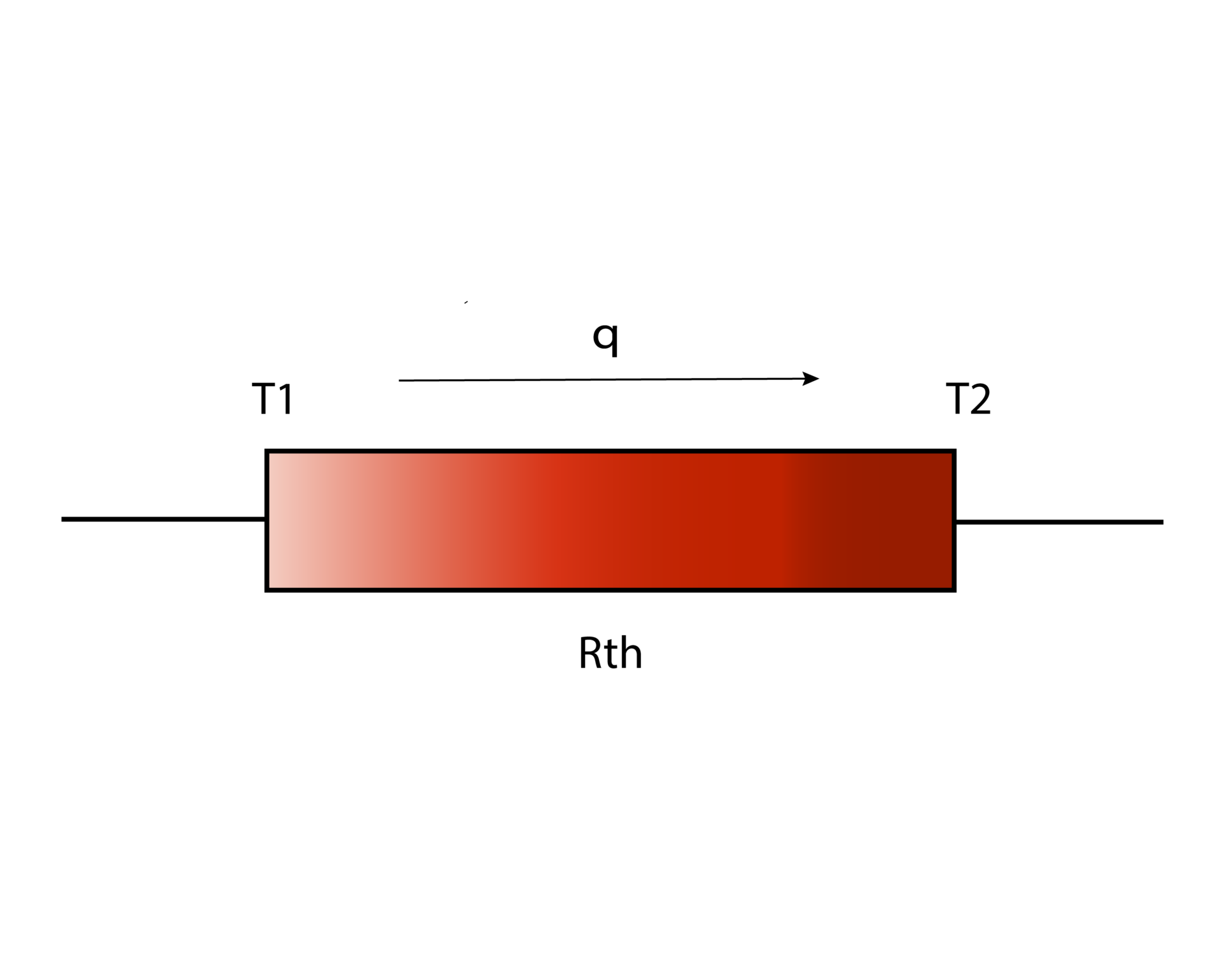
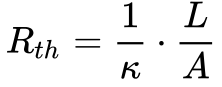
Onde:

• • L é o comprimento do material na direção do fluxo de calor [m];
  • A é a área do material normal ao fluxo de calor [m²];
  • k é a condutividade térmica do material [W/m/K];
  • R_th é a resistência térmica[K/W].

Por isso, a teoria de circuitos elétricos se aplica a resistências térmicas. Diversas resistências térmicas de um sistema podem ser agrupadas aplicando-se as mesmas regras de associação de resistências em série e em paralelo.

Inércia Térmica

O aquecimento dos materiais não ocorre instantaneamente. A temperatura da água, quando colocada numa panela no fogão, aumenta lentamente e o tempo gasto no aquecimento depende da quantidade de água na panela.

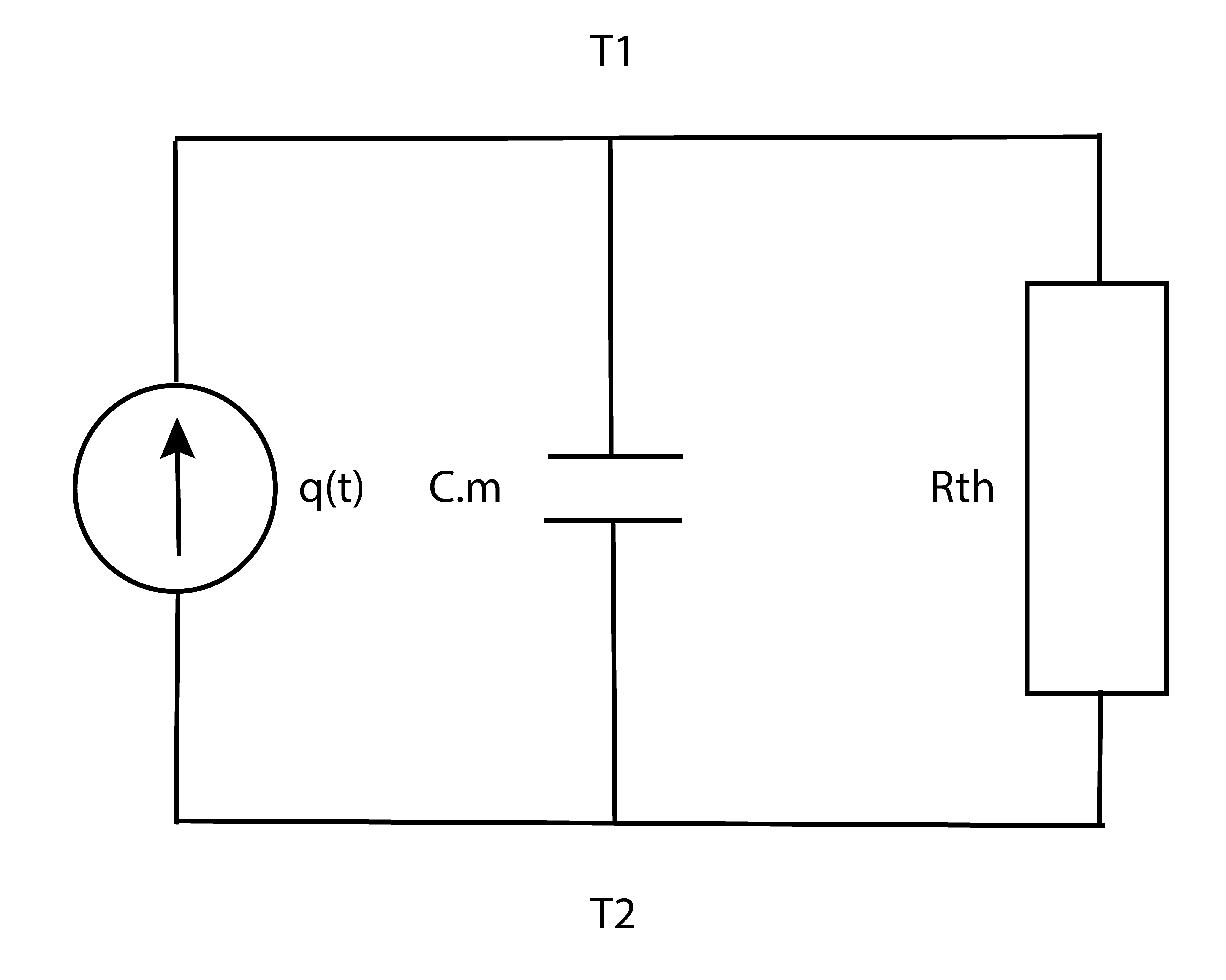
Devido à similaridade dos sistemas térmicos com os sistemas elétricos, pode-se simular este sistema térmico como um circuito RC, conforme a Figura 4.

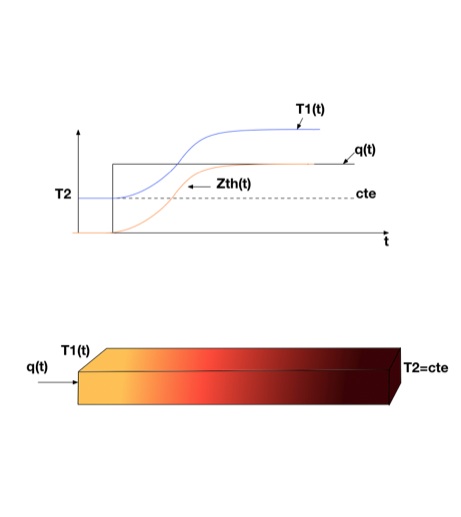
Impedância Térmica

O conceito de Impedância Térmica se baseia na Inércia Térmica.

A Figura 5 mostra este conceito. Quando se aplica um degrau de calor a um sistema térmico, a temperatura varia como a tensão T1 da Figura 3 após a aplicação de um degrau de corrente, conforme a Equação 6.

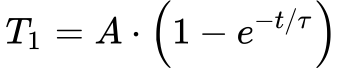
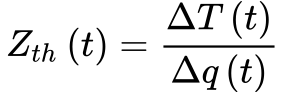
Difusividade Térmica

Define-se a Difusividade Térmica como a Condutividade Térmica dividida pela Massa Específica e pelo Calor Específico a pressão constante do material – Equação 8.

A Difusão Térmica, determinada pela expressão abaixo, se encontra relacionada com a constante de tempo térmica.

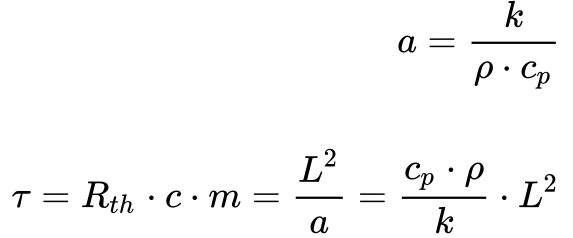
Onde:

• • a é a difusão térmica[m²/s];
  • k é a condutividade térmica[W/m/K];
  • c_p é o calor específico [W.s/kg];
  • ρ é a densidade [kg/m³];
  • τ é a constante de tempo de difusão térmica[s];
  • L é o comprimento do material no sentido do fluxo de calor[m].

Referências

1. ASHCROFT, N.W., MERMIN, N.D., Solid State Physics, Harcourt, 1976.
2. ÇENGEL, Y. A., Heat Transfer, McGraw-Hill, McGraw – Hill; 2003.
3. HAHN, D. W., OZISIK, M. N., Heat Conduction, 3 ed., Wiley, 2012.
4. KITTEL, C., Introduction to Solid State Physics, 8 Edição, Wiley, 2005.
5. TRITT, T. M., Thermal Conductivity – Theory, Properties and Applications, Kluwer/Plenum, 2004.
6. YAWS, C., Chemical Properties Handbook, McGraw-Hill,1999.