Introdução
A entropia é uma propriedade extensiva decorrente da segunda lei da termodinâmica, é apenas função do estado inicial e final de ciclos termodinâmicos, sua unidade é kJ/kg.K ou kmol/kg.K e, para sistemas reversíveis, é definida como:
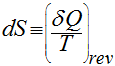
A referência da entropia, seu valor zero, é, por definição, o valor da entropia na temperatura zero absoluta. No entanto, algumas tabelas fornecem valores referentes a estados arbitrários.
A variação da entropia pode ser calculada pela integração da equação anterior desde o estado inicial até o estado final. Quando isso é feito, a definição do zero de entalpia passa a ser irrelevante.
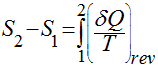
Como a entropia é uma propriedade, a sua variação entre estados independe do caminho que o processo percorreu para atingir o estado final -2 - a partir do estado inicial -1.
Equações de Gibbs
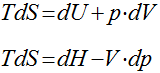
Variação de Entropia em Sólidos e Líquidos
Como os sólidos e líquidos são incompressíveis, a variação de volume é desprezível e o calor específico pode ser considerado constante. Desta maneira, as equações de Gibbs podem ser escritas da seguinte maneira:
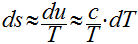
Considerando o calor específico constante, a variação da entropia pode ser calculada da seguinte maneira:
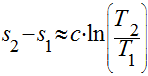
Conforme visto na seção Calor Específico, ele depende da temperatura. Portanto, se considerarmos uma aproximação linear, a variação da entropia será dada por:
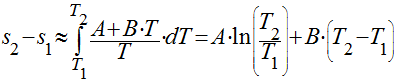
Variação da Entropia em Gases Perfeitos
A primeira equação de Gibbs pode ser escrita da seguinte maneira:
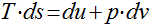
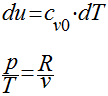
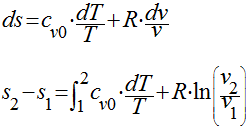
Analogamente, para a segunda equação de Gibbs, teremos que;
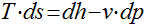
e as seguintes relações são válidas para gases perfeitos:
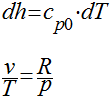
Portanto, teremos que:
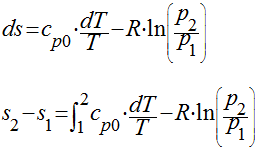
Para resolvermos estas equações é necessário conhecer a variação do calor espec�fico com a temperatura.
Existem três possibilidades para tratar deste problema:
-
Considerar o calor específico constante
Neste caso, as expressões podem ser integradas diretamente resultando em:
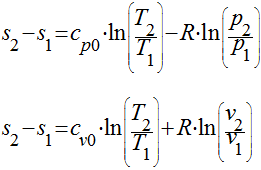
-
Considerar as expressões que aproximam o comportamento do calor específico.
Neste caso, considerando uma aproximação linear, teremos que:
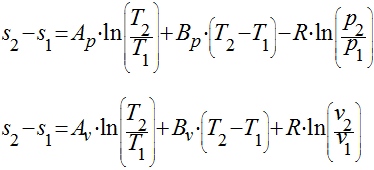
O erro cometido pela simplificação de considerar o calor específico constante dependerá das constantes específicas de cada gás e da diferença absoluta de temperatura no processo.
-
Utilizar dados fornecidos em Tabelas para os gases reais e utilizar a seguinte expressão:
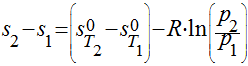
Processos Isoentrópicos
Em processos isentrópicos, as expressões anteriores são iguais a zero e, conseqüentemente, elas podem ser utilizadas para calcular as pressões e/ou os volumes específicos.
Neste caso, teremos também 3 possibilidades:
-
Calor Específico Constante
Neste caso teremos que:
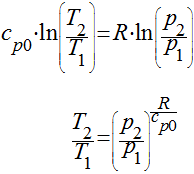
e
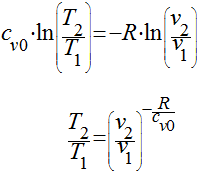
No entanto, como visto anteriormente, R=cp0-cv0, teremos que:
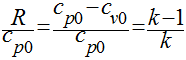
Se definirmos a relação de calor específico - k - como sendo a relação entre o calor específico a pressão constante e o calor específico a volume constante, teremos que:
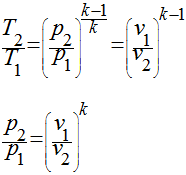
A última expressão pode ser escrita da seguinte maneira:
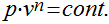
Esta expressão é válida para todos os processos adiabáticos e reversíveis que envolvem um gás perfeito com calor específico constante.
Processo Politrópico Reversível para Gases Perfeitos
Processos termodinâmicos politrópicos obedecem à relação anterior.
A expansão dos gases de combustão no cilindro de motores de combustão interna é um exemplo de processo politrópico.
O valor de n depende do tipo de processo de acordo com a Tabela abaixo.
Processo |
n |
Característica |
Isobárico |
0 |
P constante |
Isotérmico |
1 |
T constante |
Isoentrópico |
K |
S constante |
Isocórico |
∞ |
V constante |
Processos Irreversíveis
Finalmente, a expressão básica da entalpia para processos irreversíveis é dada por:
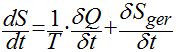
Onde:
Sger é a entalpia gerada pelo sistema devido a processos irreversíveis no interior do sistema.