Introdução
As turbinas eólicas podem ser classificadas em:
- Horizontais;
- Verticais.
As figuras acima mostram exemplos de ambos os tipos.
No entanto, fica a questão: qual a melhor turbina eólica para a geração de energia elétrica?
A principal vantagem das turbinas verticais é independer da direção do vento mas, apesar disso, as turbinas horizontais dominam o mercado atual de turbinas eólicas para geração de energia.
O principio de funcionamento das turbinas eólicas é o mesmo das turbinas hidráulicas. As diferenças são o fluído de trabalho - ar ao invés da água - e a natureza do fluxo - externo ao invés de interno.
Análise das Turbinas Horizontais
A análise das turbinas eólicas é complexa porque envolve aerodinâmica e mecânica dos fluidos.
Contudo, os conceitos básicos podem ser obtidos a partir de simplificações na análise.
A energia contida no vento horizontal é basicamente sua energia cinética, uma vez que não há variação de pressão nem variação de altitude, conforme a seguinte expressão:
![]()
Onde:
- E é a energia;
- m é a massa;
- v é a velocidade.
A expressão é extremamente simples e conhecida mas, ao tentarmos aplicá-la, surgem as algumas dificuldades:
Qual a velocidade e qual a massa a serem consideradas?
A figura abaixo apresenta uma primeira aproximação para o fluxo de ar através de um rotor de uma turbina eólica, onde:
- V∞ é a velocidade do vento muito antes de sofrer influência do rotor;
- p∞ á a pressão do ar sem sofrer influência do rotor;
- Ve é a velocidade do vento na esteira do rotor;
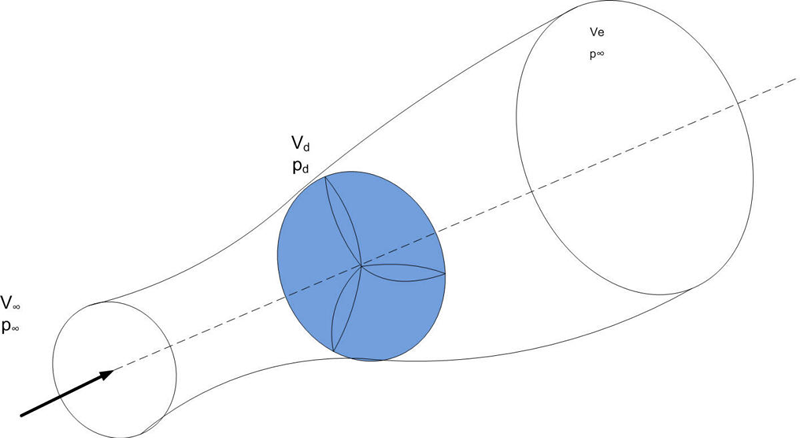
Considerando a lei da conservação da energia, a energia retirada do vento provocará uma redução na energia contida no vento após a turbina.
Isto implica na redução da velocidade do vento após o rotor e esta velocidade foi chamada de Vw. Esta velocidade está representada distante do rotor porque a presença do mesmo provoca complexas alterações no fluxo de ar.
Quanto menor for esta velocidade, maior será a energia retirada do vento e maior será o impacto ambiental.
A questão da massa a ser considerada é mais complexa.
Uma primeira aproximação é considerar apenas a massa de ar que atravessa o rotor. Desta forma, considera-se apenas a massa de ar contida no tubo fictício, apresentado na Figura anterior.
Isto significa que não existe fluxo de ar para dentro ou para fora deste duto imaginário e, conseqüentemente, a conservação de massa á aplicável a todo o duto conforme a expressão abaixo:
![]() (1)
(1)
Onde:
- ρ é a densidade do ar ;
- A é a área;
- V é a velocidade.
A velocidade no disco da turbina está relacionada com a velocidade do vento a montante através do fator de indução de fluxo axial - a - da seguinte maneira:
![]() (2)
(2)
Aplicando esta relação na equação de conservação de massa (1), teremos que:
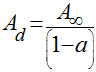 (3)
(3)
Observa-se que, devido à conservação de massa, a redução da velocidade do vento, causada pelo rotor da turbina, acarreta um aumento da área do tubo fictício proporcional ao mesmo fator de redução da velocidade.
A redução da velocidade do vento representa uma variação de momento no fluxo de ar, que é causada pela força exercida pela variação de pressão no rotor da turbina. Matematicamente, isto pode ser escrito da seguinte maneira:
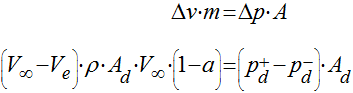 (4)
(4)
Aplicando a equação de Bernoulli às duas seções do tubo fictício, teremos que:
![]() (5)
(5)
Considerando o fluido incompressível e o sistema horizontal, teremos que:
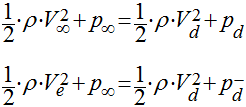 (6)
(6)
Subtraindo as equações acima, teremos que:
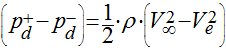 (7)
(7)
Esta expressão demonstra que a variação da velocidade do vento ocorre metade a montante e metade a jusante do rotor da turbina.
Substituindo a expressão (7) na expressão (4), teremos que:
![]() (8)
(8)
A força feita pelo vento no rotor da turbina será dada por:
![]() (9)
(9)
Conseqüentemente, a potência será dada por:
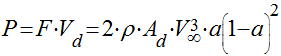 (10)
(10)
Observa-se que a potência de um gerador eólico é proporcional ao cubo da velocidade do vento e à área do rotor da turbina eólica.
Esta expressão pode ser escrita da seguinte maneira:
![]() (11)
(11)
Onde:
- ρ é a densidade do ar;
- A é a área do rotor;
- V é a velocidade do vento;
- Cp é o coeficiente de potência.
O coeficiente de potência - Cp- é definido como sendo a potência extraída pelo rotor dividida pela potência existente no vento da seguinte maneira:
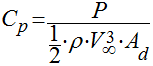 (12)
(12)
É importante observar que como a densidade do ar é 800 vezes menor do que a densidade da água, a potência de turbinas eólicas é muito menor do que a potência das turbinas hidráulicas.
O coeficiente de potência representa a fração máxima da energia contida no vento que pode ser extraída pela turbina e, combinando as expressões (11) e (12), será igual a:
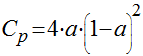 (13)
(13)
Portanto, a potência máxima possível de ser extraída do vento foi calculada por Albert Betz da seguinte maneira:
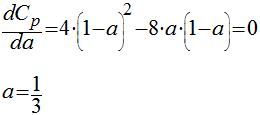 (14)
(14)
Substituindo este valor de a na eq . 13, teremos que:
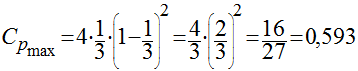 (15)
(15)
Isto significa que não é possível aproveitar mais do que 60% da potência existente no vento.
Além disso, para otimizarmos a potência eólica, é necessário operar a turbina com velocidade variável e proporcional à velocidade do vento.
A força exercida no rotor também pode ser normalizada considerando a energia do vento como base.
Desta maneira, definimos o coeficiente de torque -CT - de acordo com a seguinte expressão:
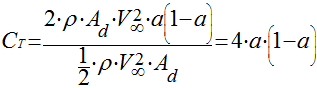
A Figura abaixo apresenta os coeficientes de torque e de potência em função de a.
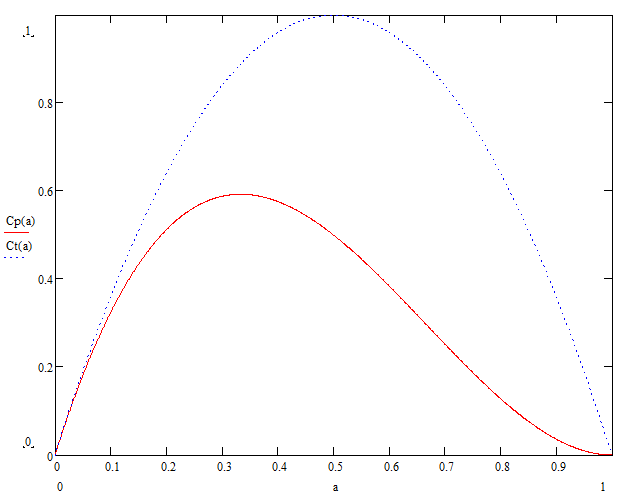
A maneira como a energia do vento é transformada em energia mecânica depende do projeto específico da turbina eólica.
No entanto, a maioria das turbinas atuais, utiliza rotores com determinado número de pás que giram com velocidade angular - ω - paralela à direção do vento e ortogonal ao plano das pás.
As pás giram ao longo da área Ap e, devido ao seu projeto aerodinâmico, criam a diferença de pressão ao longo da área que é responsável pela redução do momento no fluxo do vento e pela conversão de energia da energia do vento em energia mecânica.
O eixo do rotor da turbina é acoplado a um gerador de energia elétrica que completa a conversão da energia mecânica em energia elétrica. Neste processo, o gerador gera um torque, em sentido contrário ao torque exercido pelo vento, que é proporcional à energia elétrica gerada. Em condições de equilíbrio, estes torques se igualam e a velocidade angular permanece constante.
A geração do torque no rotor pela passagem do vento produz um torque igual e contrário no ar. Isto significa que o ar, após o rotor da turbina, adquiri um momento angular com rotação contrária à rotação do rotor, que inexistia no vento a montante da turbina.
Esta variação de momento e velocidade angular representa um aumento na energia cinética, que é compensado pela queda de pressão no ar a jusante do rotor.

