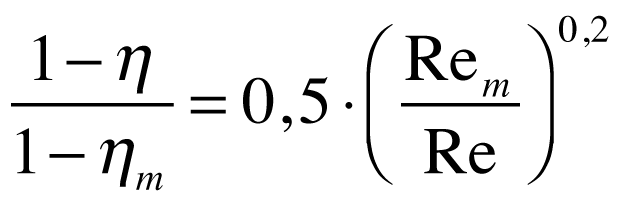Introdução
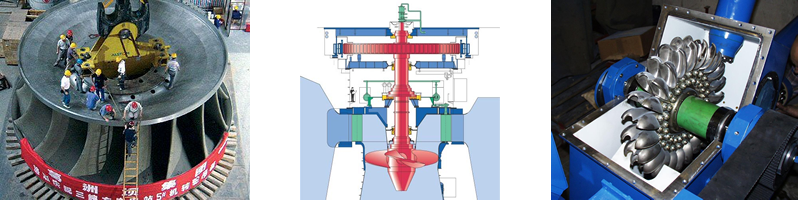
As turbinas hidráulicas transformam a energia potencial da água armazenada em reservatórios em energia mecânica.
As primeiras turbinas hidraúlicas surgiram na antiguidade com os gregos e romanos.
No entanto, as máquinas utilizadas atualmente surgiram no século 19 com o desenvolvimento da hidrodinâmica e a partir dos projetos do professor francês Claude Burdin.
| Tipo | Radial | Axial | Mista |
|
|---|---|---|---|---|
Diagonal |
Tangencial |
|||
| Ação | Francis |
Kaplan Bulbo |
Francis |
|
| Reação |
|
|
Pelton |
|
As turbinas podem ser classificadas de acordo com a direção do fluxo do fluido no rotor em:
- Axiais
- Radiais
- Mistas
Nas turbinas axiais, o fluxo da água é primordialmente paralelo ao eixo de rotação. A turbina Kaplan é um exemplo de turbina axial.
Nas turbinas radiais o fluxo é primordialmente perpendicular ao eixo de rotação. A turbina Francis é um exemplo de turbina radial.
A principal consideração é o rendimento da turbina em transformar a energia cinética da água em energia mecânica no eixo.
Anteriormente, mostramos que a energia disponível numa usina hidrelétrica está associada à energia potencial da água armazenada.
Contudo, esta energia potencial é transformada em energia cinética ao longo da tubulação até a entrada da turbina.
Por sua vez, esta energia cinética da água é parcialmente transformada em energia cinética no eixo da turbina.
As turbinas hidráulicas são extremamente eficientes mas, como manipulam enormes quantidades de energia, pequenas perdas de eficiência são significativas.
Por isso, existe uma constante preocupação com o aumento da eficiência.
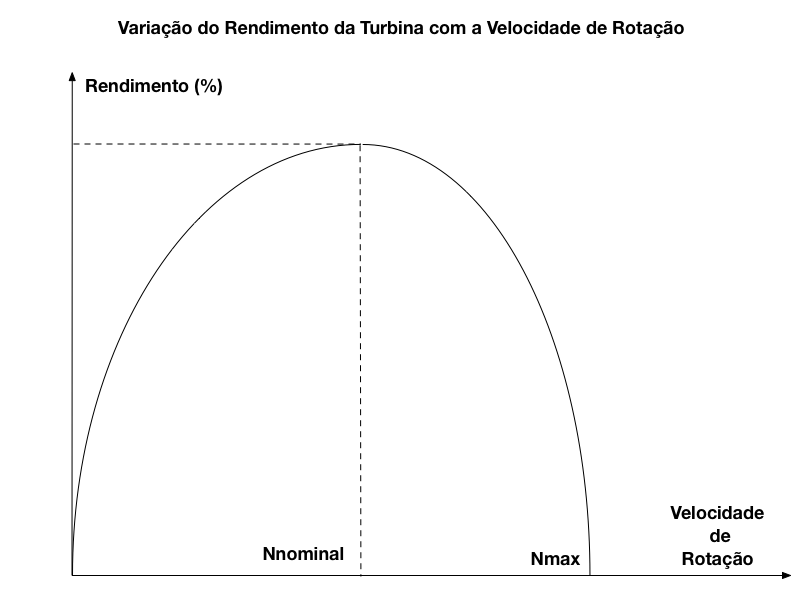
A figura abaixo apresenta a variação do rendimento da turbina hidráulica em função da velocidade de rotação.
Observa-se que o rendimento máximo está associado a uma determinada velocidade e, por isso, esta velocidade é escolhida como sendo a velocidade nominal da turbina.
Além disso, o rendimento da turbina passa a diminuir após a velocidade máxima até atingir a zero na velocidade máxima da turbina.
Como o rendimento é zero na velocidade máxima, a turbina não gera mais energia nesta condição.
Contudo, esta velocidade é extremamente importante na prática porque é representa a velocidade que a turbina atinge no caso de curto circuitos trifásicos próximos ao gerador. Por isso, esta velocidade máxima também é chamada de velocidade de disparo.
Características das Turbinas Hidráulicas
A Turbina Hidráulica é projetada para com rendimento máximo em determinadas Vazão(Q) , Queda(H) e velocidade de rotação(N) nominais.
Este rendimento é dado por:
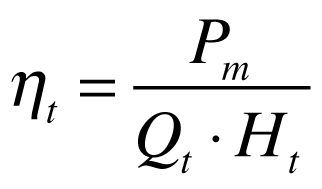
Onde:
- Pm é a potência mecânica no eixo da turbina[kW];
- ηt é o rendimento mecânico da turbina;
- Qt é a vazão na entrada da turbina[m3/s];
- Ht é a queda na entrada da turbina[m];
As curvas características das turbinas hidráulicas, incluindo seu rendimento, não podem ser determinadas teoricamente.
A vazão nas turbinas é controlada pela abertura das válvulas de controle e a figura abaixo apresenta a variação do rendimento em função da abertura de da velocidade.
Observa-se que o ponto de máximo rendimento varia com a vazão e com a velocidade de rotação.
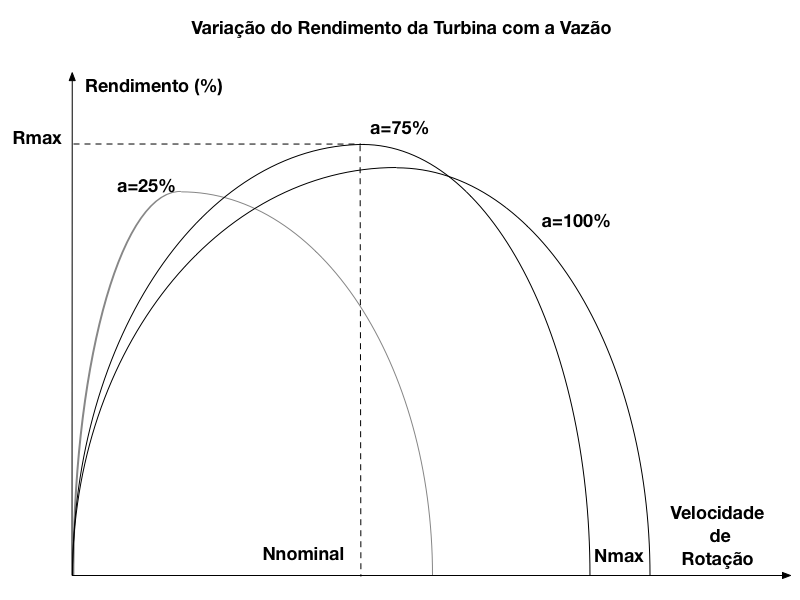
Portanto, cada curva deve ser determinada experimentalmente e, para reduzir o custo de desenvolvimento, modelos reduzidos são utilizados nessas medições.
As grandes questões são:
- Irá a máquina real se comportar como o modelo?
- Como fazer o modelo reduzido
Análise Dimensional de Turbinas Hidráulicas
A turbina hidráulica é projetada para obter o máximo de energia de uma determinada vazão Q, altura H e velocidade de rotação N.
Por isso, é fundamental conhecer do rendimento em função desses parâmetros.
As variáveis de interesse nas turbo máquinas são apresentadas na Tabela abaixo.
Grandeza |
Símbolo |
Dimensões |
Unidade |
Fluxo |
Q |
L3t-1 |
m3/s |
Energia Específica |
E |
L2t-2 |
m2/s2 |
Potência |
P |
ML2t-3 |
kg.m2/s3 |
Velocidade Rotação |
N |
t-1 |
1/s |
Dimensão |
D |
L |
m |
Densidade |
ρ |
ML-3 |
kg/m3 |
Viscosidade |
μ |
ML-1t-1 |
kg/(m.s) |
Essas variáveis podem ser agrupadas nas seguintes variáveis adimensionais:
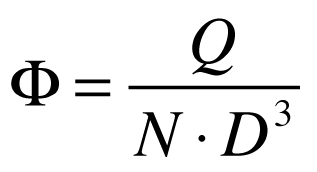
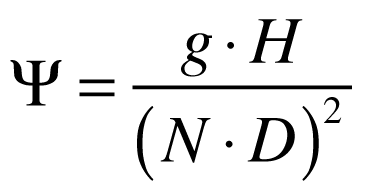
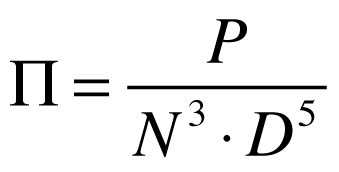
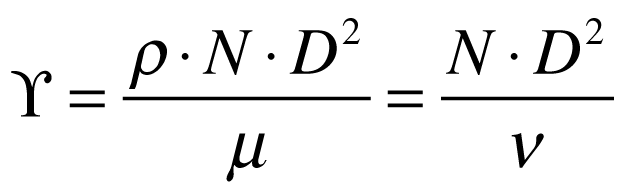
Onde:
- Φ é o coeficiente de fluxo;
- Ψ é o coeficiente de queda ou energia;
- Π é o coeficiente de potência;
- Υ é o coeficiente de Reynolds.
Combinando os coeficientes de queda e potência de modo a eliminar D, obtemos a seguinte grandeza adimensional chamada de velocidade específica.
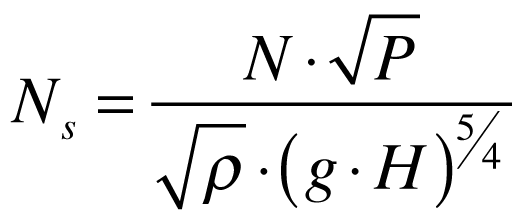
onde:
- Ns é a velocidade específica da turbina [adimensional].
Similaridade
A comparação de turbinas iguais ou geometricamente semelhantes só pode ser feita quando existe similaridade geométrica e hidrodinâmica.
Quando isto ocorre, podemos dizer que o rendimento mecânico é igual e as seguintes relações são válidas:
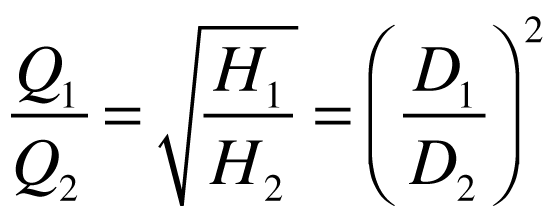
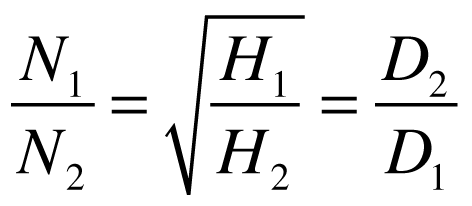
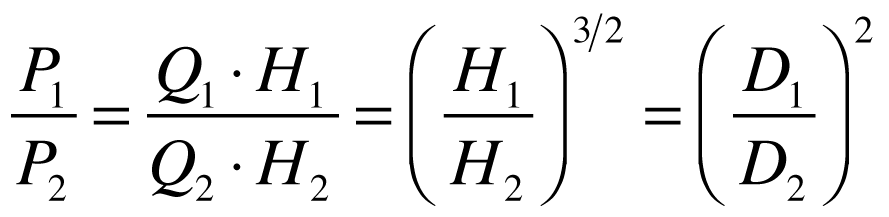
Normalização - Velocidade Específica
A base normalmente utilizada para apresentação de dados de turbinas hidráulicas utiliza a altura de queda H igual a 1 m. Por isso, as grandezas normalizadas para esta queda são chamadas de grandezas unitárias.
A partir das relações anteriores, as grandezas unitárias são dadas pelas seguintes expressões:
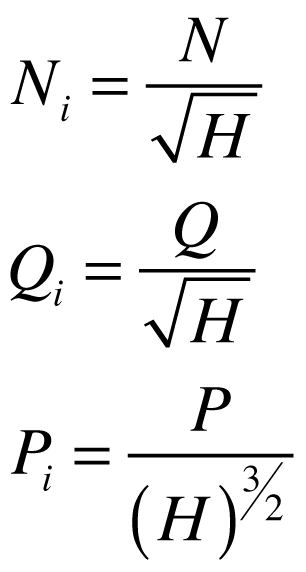
Se, nestas condições, se considerarmos a potência unitária, a velocidade específica passa a ser dada por:
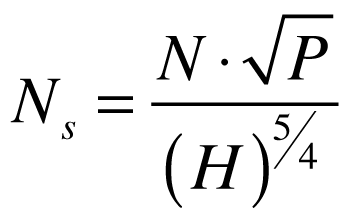
Onde:
- Ns é a velocidade específica [rpm].
Esta expressão é exatamente igual à expressão adimensional da velocidade específica mas sem a densidade da água e a aceleração da gravidade.
Contudo, cuidados especiais devem ser tomados com as unidades utilizadas porque, dependendo das unidades escolhidas, o valor numérico da velocidade específica será diferente.
Por exemplo, se utilizarmos o cv como unidade de potência, a velocidade específica será 1,166 maior do que o valor quando utilizamos kw.
A tabela abaixo apresenta as velocidades específicas e quedas normalmente utilizados para os diversos tipos de turbina.
Observa-se que, a turbinas Pelton são utilizadas em usinas de queda elevada, as turbinas Francis em usinas de queda intermediária e as turbinas Kaplan e de pás em usinas de baixa queda.
| Tipo de Turbina | Ns(rpm) | H(m) | |
|---|---|---|---|
| Pelton | 1 jato |
18 |
800 |
1 jato |
18-25 |
800-400 |
|
1 jato |
26-35 |
400-100 |
|
2 jato |
36-50 |
800-400 |
|
2 jato |
51-71 |
400-100 |
|
4 jato |
40-71 |
400-100 |
|
6 jato |
71-90 |
500-100 |
|
| Francis | muito lenta |
55-70 |
600-200 |
lenta |
71-120 |
200-100 |
|
normal |
121-200 |
100-70 |
|
rápida ou Deriaz |
201-300 |
70-25 |
|
extra-rápida |
301-450 |
25-15 |
|
| Kaplan, Bulbo, Propeller, Tubulares e Straflo | 8 pás |
250-320 |
70-50 |
7 pás |
321-430 |
50-40 |
|
6 pás |
431-530 |
40-30 |
|
5 pás |
534-620 |
30-20 |
|
4 pás |
624-.. |
30 |
|
Normalização - Velocidade Padrão
Conforme visto anteriormente, a utilização da velocidade específica requer a medição ou conhecimento da potência da turbina. Isto nem sempre é possível, principalmente durante o desenvolvimento da turbina.
Por isso, alguns autores utilizam a vazão de 1m3/s ao invés da potência 1cv (ou outra unidade de potência) como base para normalizar as grandezas da turbina.
Neste caso, teremos que:
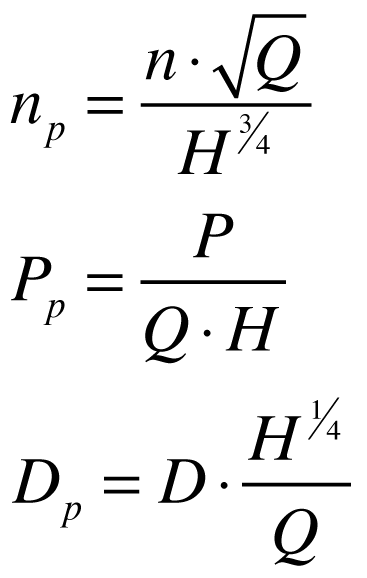
Portanto, a relação entre a velocidade específica e a velocidade padrão será dada por:
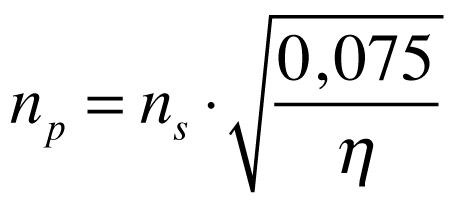
Observa-se que a relação entre as duas grandezas é o rendimento e esta expressão é válida para correlacionar valores de ns calculados em cv.
Normalização - Velocidade periférica
Do ponto de vista de mecânica dos fluidos, mais importante do que a velocidade de rotação é a velocidade periférica da turbina.
Por isso, alguns autores utilizão a velocidade específica em função da velocidade periférica.
A velocidade periférica é dada pela seguinte expressão:
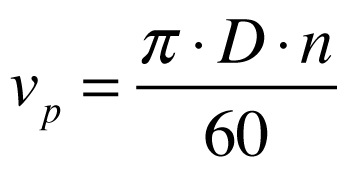
Onde:
- D é o diâmetro do rotor da turbina[m];
- n é a velocidade de rotação da turbina[rpm]
Substituindo o valor da velocidade de rotação, obtida a partir da expressão acima, na expressão da velocidade específica, teremos que:
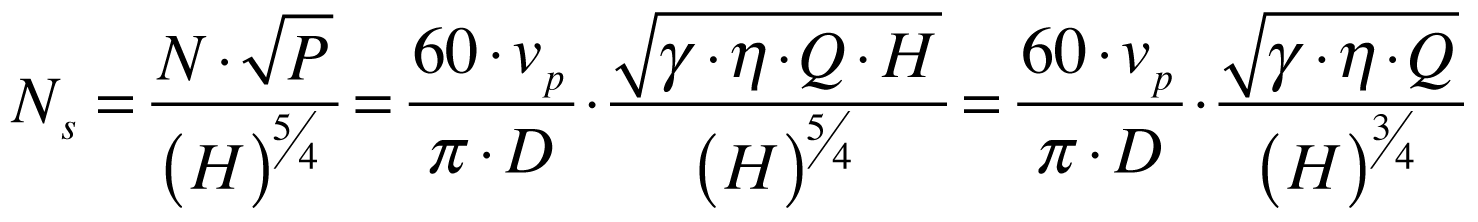
Multiplicando o numerador e denominador por g teremos que:
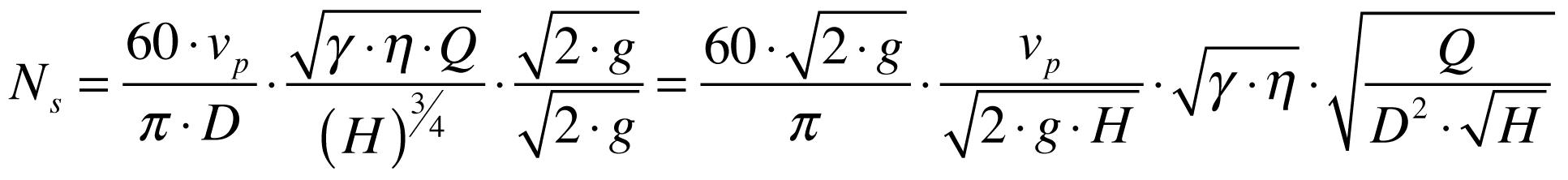
Definindo o coeficiente de velocidade periférica da turbina como sendo a velocidade periférica dividida pela velocidade do teorema de Torricelli,
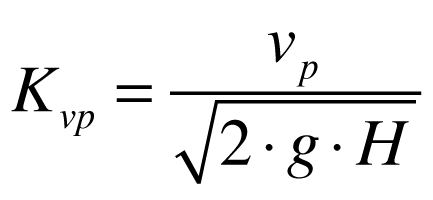
e o fator de engolimento da turbina como sendo:
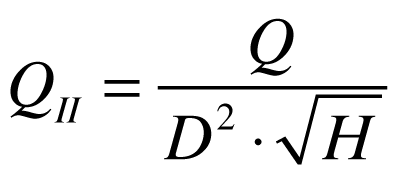
A velocidade específica será dada por:
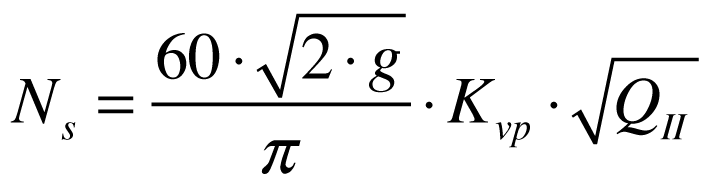
Como o coeficiente de velocidade periférica é um dado conhecido de projeto das turbinas, utiliza-se esta expressão para determinar o diâmetro da turbina.
Fórmulas de Correção do Rendimento
Na prática, a modelagem de protótipos e modelos em escala apresenta alguns erros. Por isso,existem diversas fórmulas empíricas que procuram corrigir estes erros. As mais utilizadas encontram-se a seguir.
Moody
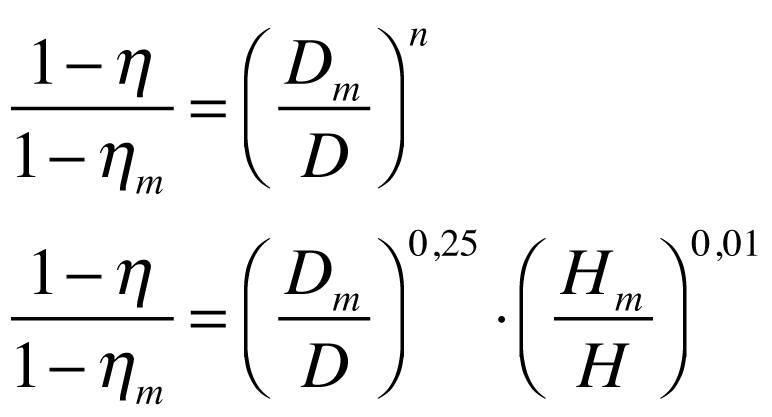
Onde:
- O índice m representa a grandeza do modelo.
- n é igual a 0,20
Estas expressões sAo aplicáveis apenas para turbinas de reação - Francis.
Pfleiderer
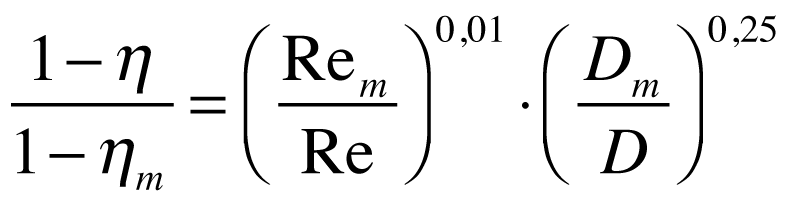
Hutton
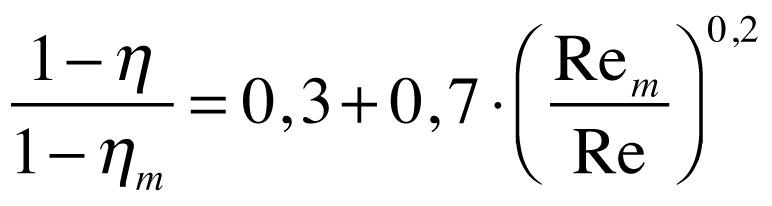
A expressão de Hutton deve ser aplicada apenas a turbinais axiais.
Ackeret