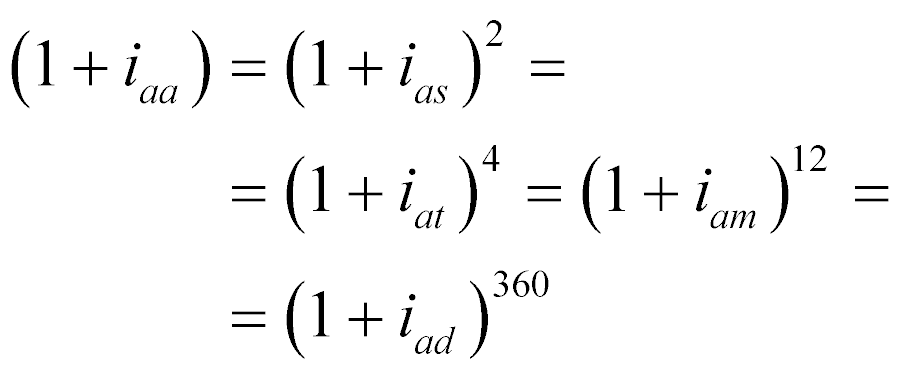Introdução
Independentemente da profissão, a matemática financeira é básica para a vida cotidiana de todos nós.
Ela serve tanto para o milionário decidir o melhor investimento de bilhões como para o cidadão comum verificar se a prestação cobrada na compra de um eletrodoméstico deve ser aceita ou não.
Contudo, por razões obscuras, seu ensino é limitado aos cursos de nível superior relacionados à área de finanças.
Até mesmo nos cursos de engenharia, ela muitas vezes não tem mais sido ensinada.
A matemática financeira não requer conhecimento prévio de cálculo diferencial e ou integral e poderia fazer parte do ensino médio.
O princípio básico da matemática financeira é o conceito do valor do dinheiro no tempo.
Todos nós conhecemos intuitivamente este princípio.
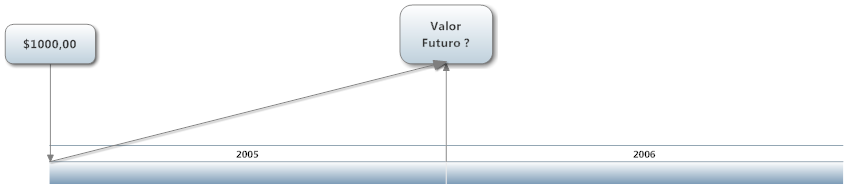
A figura abaixo apresenta o conceito de valor futuro do dinheiro.
Quanto maior o tempo maior o valor futuro do dinheiro mas como medir a velocidade deste aumento?
Esta velocidade poderia ser expressa em $/ano ou em $/mês, onde $ pode ser qualquer unidade monetária.
No entanto, dependendo do valor inicial, esta velocidade teria um valor relativo diferente.
Por isso, esta velocidade é normalizada tendo como base a quantidade de dinheiro existente no instante de referência, que pode ser qualque umr. A escolha do tempo de referência dependerá da situação específica.
Se, no caso da figura anterior, a velocidade de aumento do valor do dinheiro fosse de R$100,00 por ano, a velocidade normalizada seria de 10% ao ano.
Portanto, o conceito de velocidade de aumento de valor depende do tempo considerado, da mesma forma que o valor numérico da velocidade de um carro depende da unidade de tempo utilizada.
Portanto, o valor futuro é igual ao valor inicial mais o incremento relativo à velocidade de aumento.
Neste momento surge o primeiro conflito de interesses.
Quando investimos nosso capital, queremos a maior velocidade de crescimento possível.
Por outro lado, quando pegamos capital emprestado, queremos a menor velocidade de crescimento possível.
Como o dinheiro é uma mercadoria escassa, podemos aplicar as leis de oferta e procura da economia e, consequentemente, esta velocidade de crescimento de capital será determinada pelas condições de mercado.
A velocidade de crescimento de capital é chamada de taxa de juros, em operações de empréstimo, ou de taxa de retorno, em operações de investimento.
A matemática financeira se aplica a ambas e, em função disso, chama-se de juros a velocidade de crescimento de capital independentemente da operação. Isto pode causar confusão em alguns casos.
Valor Futuro
Portanto, o valor futuro está relacionado com o valor presente da seguinte maneira:
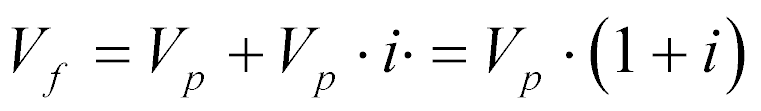 (1)
(1)
Onde:
- Vf é o valor futuro[$];
- Vp é o valor presente[$];
- i é a taxa de juros(pu);
Esta expressão só é válida quando a taxa de juros tem como base a mesma unidade de tempo do valor futuro.
Isto significa que a taxa de juros, normalmente expressa em percentual, precisa conter a informação da base de tempo.
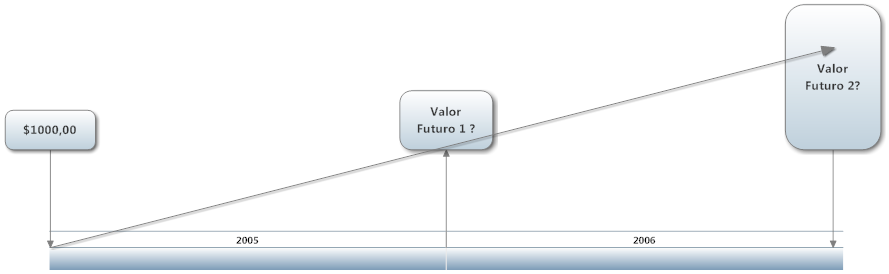
Quando isto não é verdade, surge a questão da capitalização dos juros, conforme mostra a figura abaixo.
O valor futuro 2 pode ser calculado, supondo a taxa de juros constante, a partir da expressão (1) da seguinte maneira:
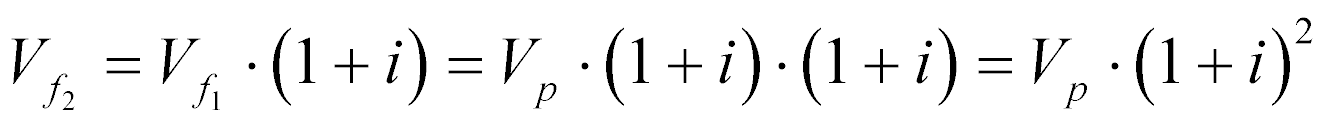
Analogamente, o valor futuro no período n, supondo a taxa de juros constante, pode ser escrito da seguinte maneira:
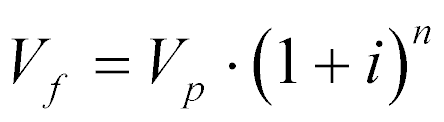 (2)
(2)
Esta expressão considera a aplicação de juros compostos e é universalmente utilizada mas ainda causa muitos problemas políticos.
A quantidade de juros normalizados em relação ao valor presente paga neste sistema é dada por:
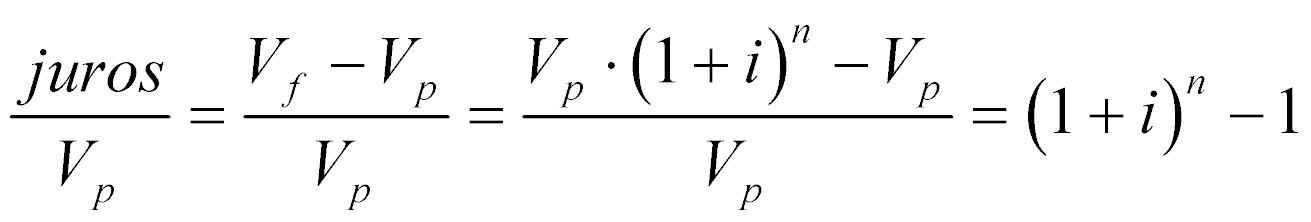
Observamos que os juros pagos crescem exponencialmente com o número de períodos de capitalização.
Valor Presente
A partir da expressão (2), podemos escrever que o valor presente será dado por:
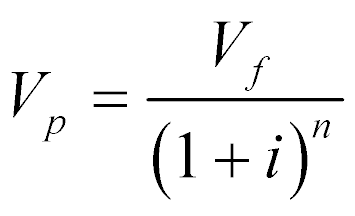 (3)
(3)
Sistema de Pagamentos Uniformes
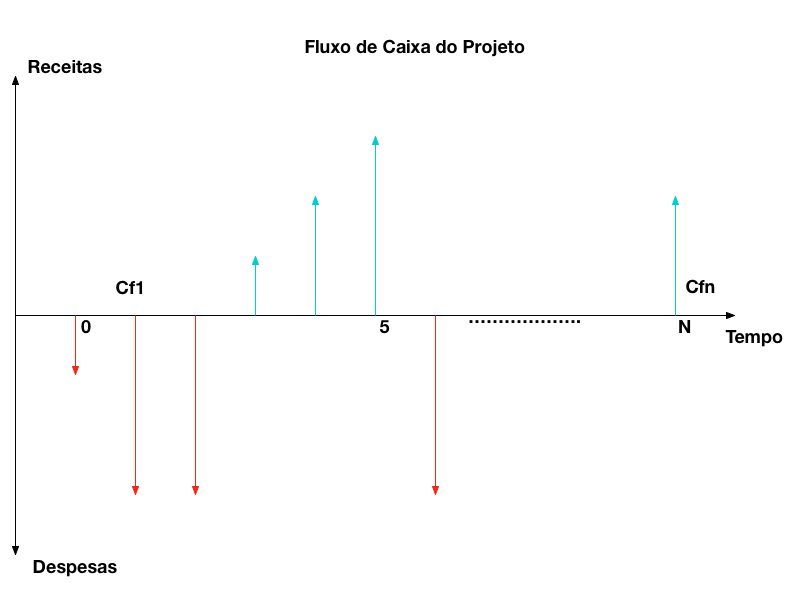
O sistema e pagamentos ou recebimentos periódicos é muito utilizado na prática.
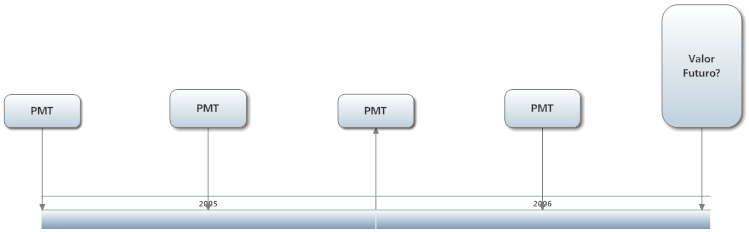
Neste sistema, conforme mostra a figura abaixo, pagamentos são feitos ou recebidos com a mesma periodicidade durante um total de n períodos. A questão é determinar o valor futuro e o valor presente deste fluxo de caixa.
Aplicando a expressão(2), teremos que:
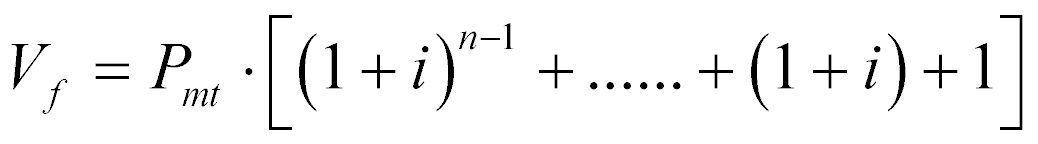 (4)
(4)
Se multiplicarmos ambos os lados da equação por (1+i), teremos que:
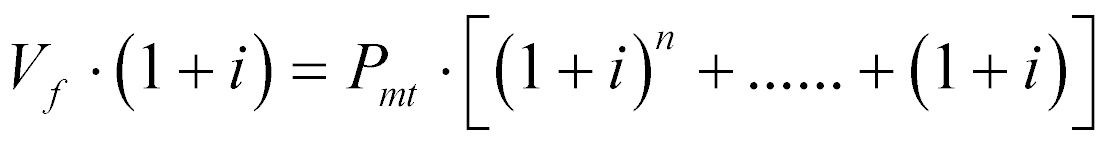 (5)
(5)
Subtraindo a expressão (5) da (4), teremos que:
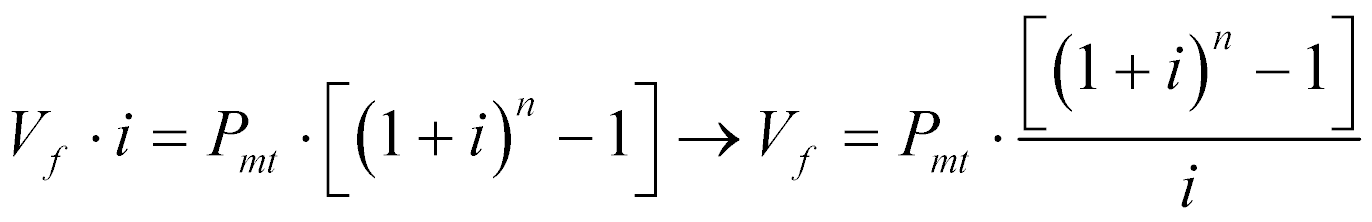 (6)
(6)
Consequentemente, o valor presente será dado pela aplicação da relação (3):
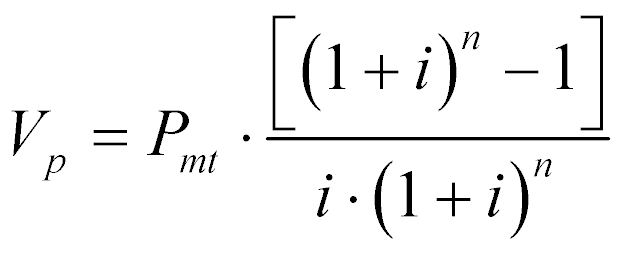 (7)
(7)
Normalização
Todas as expressões acima têm dimensão de unidades monetárias $.
No entanto, em muitos casos é mais conveniente trabalhar com estas expressões normalizadas.
A questão é a escolha da base. Qualquer um dos valores - Vf, Vp ou Pmt - podem ser utilizados como base.
Contudo, para as aplicações de geração de energia, que envolvem investimentos elevados, utiza-se normalmente o valor presente como base. Neste caso, as equações serão escritas da seguinte maneira:
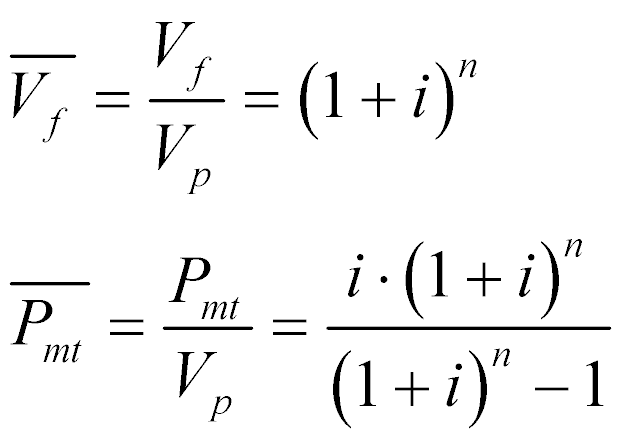
Análise de Viabilidade de Projetos
O grande problema da análise de projetos e/ou da tomada de decisão de investimentos é a comparação entre as possíveis opções.
Por exemplo:
- É melhor construir uma hidrelétrica ou uma termelétrica?
- Qual o investimento máximo que podemos fazer para um determinado investidor?
- Dado o valor do investimento necessário para a construção de uma usina, qual deve ser o preço da energia vendida?
Os conceitos de valor presente líquido, taxa de desconto e equivalência de fluxos de caixa são conceitos relacionados.
Valor Presente Líquido
Valor Presente Líquido - VPL - de um fluxo de caixa é o valor monetário equivalente de todo o fluxo no instante de tempo atual ou no início do empreendimento.
Para calcular este valor é necessário somar as receitas líquidas futuras descontadas para o valor presente com uma deterninada taxa de desconto.
As receitas líquidas são as receitas menos as despesas em determinado intervalo de tempo.
A taxa de desconto não é a taxa de juros cobrada pelo banco para emprestar dinheiro para o projeto e/ou investidor.
A taxa de desconto está relacionada com a taxa de lucratividade do projeto, tem de ser maior do que a taxa de juros do empréstimo e depende do investidor.
A escolha da taxa de desconto é extremamente importante porque, dependendo dela, determinado projeto passará a ser prioritário com relação a outro.
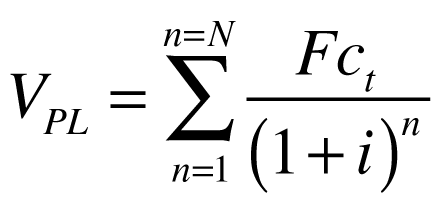
Onde:
- Vpl é o valor presente líquido;
- Fc é o fluxo de caixa no tempo t;
- i é a taxa de desconto;
- n é o período de tempo.
O cálculo do VPL é simples e pode ser feito manualmente com uma calculadora.
A grande questão é; qual a taxa de desconto que devemos utilizar?
A resposta para esta pergunta não é simples e depende do investidor que pretende fazer o projeto.
De uma maneira geral, a taxa a ser utilizada deve ser maior do que a taxa de retorno dos investimentos seguros disponíveis para este investidor. Porém, não existe um valor máximo.
Além disso, seu resultado é em unidades monetárias. Isto significa que a comparação de investimentos de valores muito diferentes não pode ser feita apenas com o VPL.
Taxa Interna de Retorno
Por causa dos problemas com o VPL, criou-se a Taxa interna de Retorno.
A Taxa Interna de Retorno - TIR - é definida como sendo a taxa de desconto que faz com que o valor presente de determinado fluxo de caixa seja zero.
Isto significa que, para este fluxo de caixa e com esta taxa de desconto, a receita líquida do projeto permite apenas o pagamento do investimento.
Para calcular a TIR, é necessário resolver a equação abaixo. Infelizmente, esta equação não tem solução analítica e só pode ser resolvida numericamente utilizando-se as técnicas de cálculo numérico.
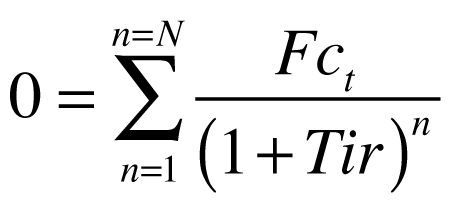
Onde:
- Fc é o fluxo de caixa no tempo t;
- Tir é a taxa interna de retorno;
- n é o período de tempo.