Introdução
Conforme visto anteriormente, a pot�ncia de toda usina hidrelétrica é proporcional à vazão de água disponível para movimentar as turbinas.
Esta vazão é o escoamento superficial medido em determinados pontos ou o calculado a partir dos modelos hidrol�gicos.
A vaz�o afluente é definida como sendo a vazão que chega a um determinado ponto, em particular um aproveitamento hidrelétrico, e é determinante na avaliação da energia disponível. A vazão afluente depende das condições hidrológicas naturais da bacia hidrográfica e dos aproveitamentos existentes a montante.
Quando inexistem aproveitamentos hidrelétricos a montante ou eles operam com nível constante, esta vazão é chamada de vaz�o natural afluente, ou seja, é a vazão que existia naturalmente antes de qualquer intervenção humana.
Portanto, imaginemos um país começando a desenvolver seu parque de geração.
Neste caso, a análise da viabilidade dos aproveitamentos inicia-se com o estudo da vazão natural uma vez que inexistem outros aproveitamentos. Este também é o caso do primeiro aproveitamento de uma bacia hidrográfica.
Análise Estatística das Vazões
A vazão é medida em determinados pontos dos rios das diversas bacias hidrográficas. A série das medições de cada ponto forma um conjunto de dados horários, diários ou mensais.
A grande questão neste capítulo é como analisá-los para a geração de energia.
O ONS fornece relatórios anuais com os dados de medições mensais e diárias das vazões naturais de todas as usinas em operação a partir de 1931.
A Tabela em anexo apresenta os dados das médias mensais da vazão natural relativos à usina de Três Marias nos últimos 76 anos. Observa-se que estão organizados de forma matricial em função dos anos e dos meses.
Estes dados podem ser apresentados por mês, conforme mostra a Figura abaixo e são s�ries temporais.
A primeira conclusão é o comportamento cíclico anual da vazão.
Esse comportamento pode ser melhor visualizado na figura abaixo, que mostra apenas os valores mensais máximos, médios e mínimos.
A partir da curva das médias mensais e da Média de Longo Prazo(MLT), definimos o período seco e o período úmido.
Quando a média mensal está abaixo da MLT, estamos no período seco.
Caso contrário, estamos no período úmido.
Observa-se claramente que, no caso de Três Marias, o período seco inicia em abril e termina em novembro.
Estas datas dependem principalmente da bacia hidrográfica e da localização geográfica do aproveitamento.
Médias Máximos e Mínimos
A próxima figura apresenta os valores anuais médios, máximos e mínimos das vazões.
Observa-se que não existe um comportamento cíclico plurianual e as variações parecem mais aleatórias. No entanto, existem períodos de anos seguidos acima da média e anos seguidos abaixo da média.
Isto sugere a hipótese de que as vazões podem ser consideradas séries temporais estacionárias.
Esta hipótese permite uma série de simplificações matemáticas nos modelos a serem utilizados mas pode não ser verdadeira.
Por exemplo, os fenômenos do El Niño e da La Niña podem fazer com que estas séries não sejam mais estacionárias assim como o aquecimento global.
Os dois primeiros fenômenos podem acrescentar um comportamento periódico de frequência ainda não determinada mas com período de vários anos.
Porém, no caso de mudanças climáticas, a série de vazões deixa de ser estacionária e o comportamento energético de nossas usinas será afetado de maneira ainda desconhecida.
Observa-se que as maiores vazões médias mensais registrada em Três Marias foram em 1979, 1983, 1992, 1997 e 2007.
Por outro lado, as menores vazões médias mensais ocorreram em 2001, 1954 e 1936.
Normalização da Vazão
Trabalhar com os dados de vazão em m3/s não é muito conveniente para a comparação entre diversos rios e aproveitamentos.
Por isso, é conveniente normalizar a série de vazões com relação à média, conforme mostra a figura abaixo.
Observa-se que a máxima vazão anual observada em Três Marias foi de 6,44 pu e a mínima 0,08 pu.
Isto nos leva a um intervalo de vazões (Qmax-Qmin) de 6,36 pu.
A grande questão é; é este comportamento normal para todos os rios ou é característica apenas do São Francisco em Três Marias?
Para tentar responder a esta pergunta, a figura abaixo apresenta as vazões normalizadas de Simplício.
Apesar dos rios apresentarem vazão média próximas, Três Marias apenas 23% maior, os valores máximos anuais normalizados são de 3,83 e 6,44 pu respectivamente.
Além disso, as vazões mínimas anuais normalizadas são de 0,29 pu e 0,08 pu respectivamente.
Com isso, o intervalo de vazões de Três Marias é de 6,36 pu enquanto o de Simplício é de 3,54 e o desvio padrão de Três Marias é 0,96 pu enquanto o de Simplício é de 0,58 pu.
A partir desses números, pode-se concluir que a vazão de Três Marias varia mais do que a vazão de Simplício, ou seja, ela é mais volátil.
Será que isto ocorre apenas com Três Marias?
O célebre video dos artistas globais sobre Belo Monte falava sobre isto.
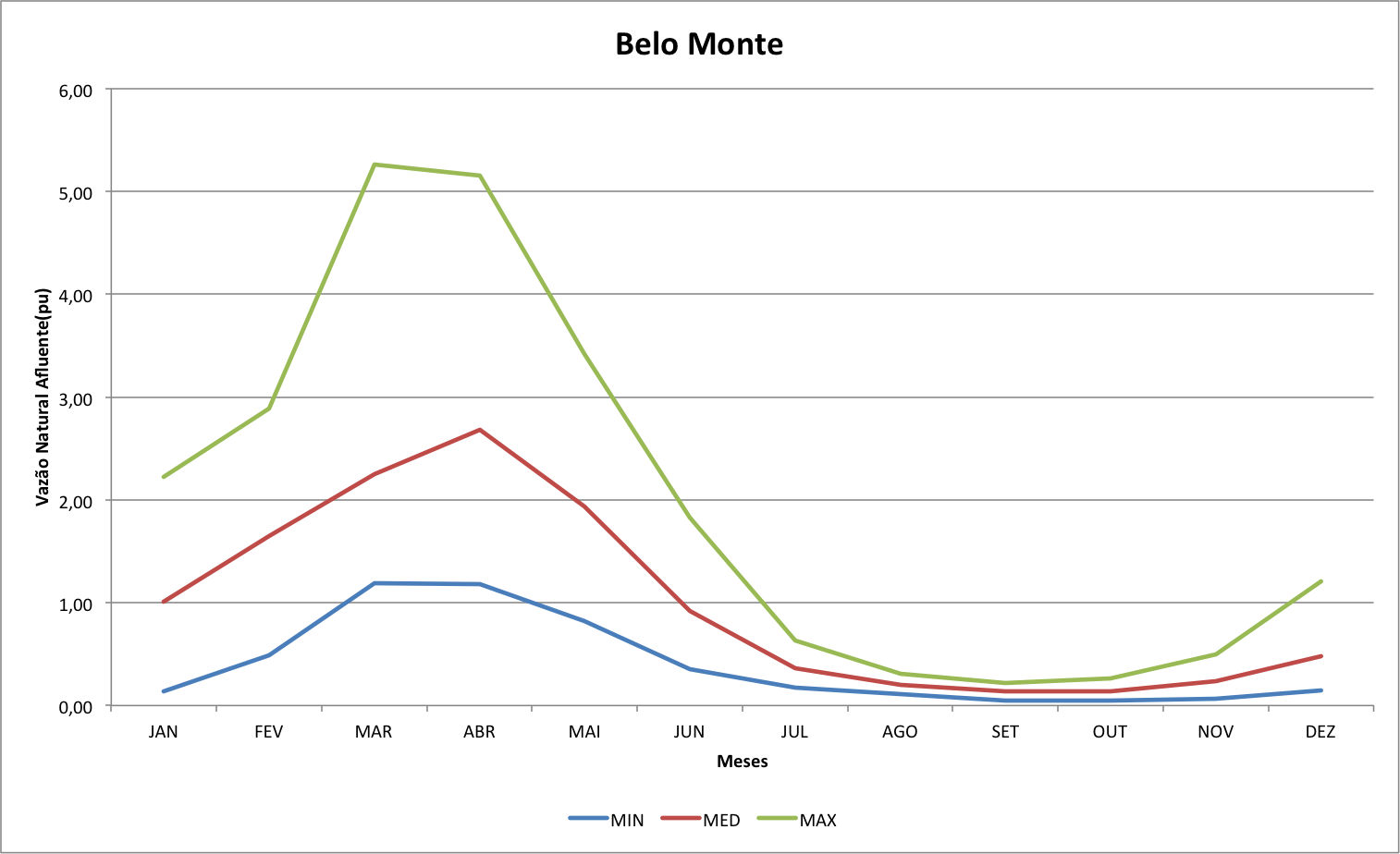
A figura abaixo mostra as vazões máximas, médias e míminas das vazões médias mensais da série histórica de 80 anos da vazão natural afluente de Belo Monte.
Observa-se que as vazões durante o período de seca são inferiores a 50% da MLT. Isto significa que, como Belo Monte será uma usina a fio d'água devido à restrições ambientais, alguma outra usina deverá gerar durante o período de seca.
Além disso, o sistema de transmissão, especialmente projetado e construido para Belo Monte, ficará subutilizado durante metade do ano.
Densidade de Probabilidade
Portanto, a primeira coisa a ser feita ao se lidar com dados de vazão é descobrir seu comportamento estatístico.
A figura abaixo apresenta a distribuição de probabilidade das vazões médias mensais normalizadas de Três Marias.
Observa-se que ela não pode ser, a priori, classificada como nenhuma das distribuições normalmente utilizadas mesmo com a grande quantidade de pontos utilizados.
A distribuição acumulada nos fornece a probabilidade da vazão ser inferior a um determinado valor.
Além disso, observa-se um forte crescimento na densidade de probabilidade antes de atingir seu máximo e um lento declínio para vazões superiores.
Este comportamento é típico em grandezas físicas que não podem ser inferiores a zero mas que não possuem restrição física para seu máximo.
É importante observar que, no caso de Três Marias, a probabilidade acumulada de vazões inferiores à MLT, que corresponde a 1 pu, é de 66%. Isto significa que em 66% do tempo a vazão mensal neste reservatório é inferior à média.
A Figura abaixo apresenta a comparação entre as densidades de probabilidade das vazões médias mensais normalizadas de Três Marias e Simplício.
Observamos que a forma das distribuições são parecidas mas os parâmetros estatísticos são diferentes.
Persistência
Outra maneira muito comum de se apresentar os dados de vazão é através da curva de persistência mostrada abaixo.
No eixo dos x é o complemento da distribuição acumulada do histograma.
Este valor tem o significado do tempo em que a vazão, apresentada no eixo y, é superior a um determinado valor.
A partir da curva de persistência é possível calcular a probabilidade da vazão ser superior ou inferior a um determinado valor.
Esta curva pode ser aproximada pela seguinte equação:
![]()
Onde:
- Q é a vazão normalizada;
- t é o tempo, em percentual;
- A e B são constantes.
As constantes podem ser determinadas da seguinte maneira:
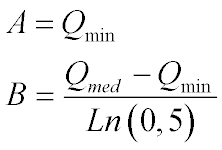
Onde:
- Qmin é a vazão mínima;
- Qmed é a vazão mediana (50% probabilidade).
Caso queiramos maior precisão na aproximação, os parâmetros A e B podem ser estimados pela técnica de minimização do erro quadrático.
Distribuição de Energia
Outra questão importante é a distribuição da energia para cada nível de vazão.
Vazões elevadas podem gerar muita potência mas, se sua duração for pequena, a energia associada será pequena.
A curva de persistência fornece a vazão e a duração.
Como a vazão é proporcional à potência, podemos criar um novo gráfico que tem o produto da vazão pela persistência no eixo dos y e a própria vazão no eixo dos x.
Como a persistência tem dimensão de tempo ou duração, seu produto pela vazão passa a ter dimensão de energia.
Este gráfico pode ser chamado de probabilidade de energia.
Cada barra apresenta a energia associada à respectiva a vazão.
Com esta informação, é possível determinar a quantidade de máquinas ideal para um determinado aproveitamento.
Análise das Vazões Extremas
Outra questão importante na análise das vazões, é a análise dos valores extremos. Isto é, os valores máximos de vazão e os valores mínimos possíveis de serem observados.
Estes valores são importantes no projeto dos empreendimentos e na operação dos reservatórios.
Na análise dos valores extremos devemos utilizar dados de vazão obtidos com maior frequência. Por isso, as séries de vazões médias mensais são inadequadas.
A Tabela apresenta a estatística descritiva da série de vazões médias diárias normalizadas de Três Marias. Observa-se que os valores máximos e mínimos são muito diferentes dos obtidos a partir das médias mensais.
A figura abaixo apresenta a densidade de probabilidade das vazões médias diárias de Três Marias superiores a 2,71 pu e a aproximação utilizando-se a função de Gumbel.
Observa-se que a função de Gumbel é uma ótima aproximação para estas vazões extremas.
Volume
Outra questão muito importante é qual o volume de água que devemos e/ou podemos armazenar para regularizar a vazão.
Para isso, definimos o volume base anual como sendo o volume de água médio anual, que é igual à vazão média de longo prazo em m3/s vezes o número de segundos no ano (31.536.000 s).
Isto significa que cada metro cúbico por segundo por ano corresponde ao volume de 0,031536 km3.
Para responder a esta questão devemos considerar as equações do balan�o h�drico.
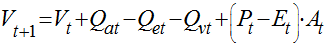
Onde:
- Qat é a vazão afluente no instante t;
- Vt é o volume do reservatório no instante t;
- At é a área da superfície do reservatório no instante t;
- Pt é a precipitação no reservatório no instante t;
- Et é a evaporação do reservatório no instante t;
- Qet é a vazão efluente turbinada no instante t;
- Qvt é a vazão efluente vertida no instante t.
Como estamos trabalhando apenas com os dados de vazão em um determinado ponto, podemos simplificar esta equação desprezando a precipitação, a evapotranspiração e o fluxo subterrâneo. Desta maneira, teremos que:
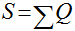
Isto significa que basta somarmos as vazões médias mensais normalizadas. No entanto, com as vazões são sempre positivas, este número será sempre crescente e sua análise torna-se complexa e inexata.
Este método é conhecido como diagrama de Rippl ou de massas e foi desenvolvido no século passado antes das ferramentas computacionais modernas.
Para melhorar a sensibilidade da análise, é mais conveniente trabalhar com as variações das vazões em relação à MLT.
A figura abaixo mostra o somatório anual das variações diferenciais mensais, chamado de volume diferencial anual, e o seu somatório, chamado de volume diferencial anual acumulado.
O volume diferencial anual foi arbitrariamente definido como sendo o somatório das vazões mensais normalizadas do ano em questão menos a vazão anual média normalizada que é sempre igual a 12, pois este é o número de meses no ano.
O objetivo desta definição é procurar observar apenas as variações de vazão entre os sucessivos ciclos hidrológicos anuais.
Desta maneira, capturamos apenas variações plurianuais e desprezamos as variações anuais já estudas.
Por definição, o volume em t=0 é considerado igual a zero.
Como o volume diferencial anual é um somatório de valores normalizados, ele também é um valor normalizado.
Conforme esperado, os volumes diferenciais anuais oscilam entre valores positivos e negativos uma vez que a média desses valores é zero por definição. Além disso, como seu valor inicial foi considerado igual a zero, seu valor final também será igual a zero.
Com este gráfico podemos determinar os anos de maiores afluências e os de menores afluências.
No caso específico de Três Marias, 1983 foi o ano com maior volume de águas e 2001 foi o ano com menor volume diferencial anual.
Observamos que enchentes ocorreram periodicamente a cada 13/16 anos e secas ocorreram em maior número, mas com periodicidade aleatória entre 11 e 19 anos.
Por outro lado, observamos que, para este aproveitamento, os anos de 1953 a 1960 e de 1998 a 2003 foram todos abaixo da média. Isto ajuda a explicar um pouco o racionamento de 2001.
Apesar dos gráficos apresentarem dados normalizados, é importante ressaltar que a base mudou para o volume base anual.
Para calcular este gráfico deve-se subtrair a média de cada vazão média mensal normalizada e fazer o somatório desta diferença conforme a expressão abaixo. Ao mês de janeiro de cada ano foi somado o mês de dezembro do ano anterior.
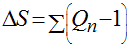
O segundo gráfico mostra a variação acumulada dos volumes diferenciais anuais.
Observamos claramente que os ciclos hidrológicos são plurianuais e, conseqüentemente, reservatórios com volumes consideráveis seriam necessários para regularizar esta vazão.
Em função do apresentado, concluímos que os aproveitamentos hidrelétricos estão sujeitos a variações extremas de vazão devido ao comportamento cíclico anual, originado pelos períodos úmido e seco e por variações de longo prazo ainda não modeladas corretamente.
Estas características são comuns a todos aproveitamentos hidrelétricos e nos leva às seguintes questões:
1. Qual a maior carga que está usina poderá alimentar sozinha continuamente durante todo o ano?
2. Qual o risco de não haver água suficiente em determinado ano para alimentar esta carga?
3. Como aproveitar a água excedente durante os anos ou meses de maior vazão?
4. Qual o risco de vazões superiores às vazões registradas?
Estas perguntas serão tratadas no capítulo Projetos Hidrel�tricos.



